Знак разделить как пишется

Самый старый знак деления скорее всего знак ( / ) . Впервые его использовал английский математик Уильям Отред в своём труде Clavis Mathematicae (1631, Лондон).

Немецкий математик Лейбниц предпочитал двоеточие ( : ) . Этот символ он использовал впервые в 1684 году в своём труде Acta eruditorum. До Лейбница этот знак был использован англичанином Джонсоном в 1633 году в одной книге, но как знак дроби, а не деления в узком смысле.

Немецкий математик Йоханн Ран ввёл для обозначения деления знак ( ÷ ) . Вместе со знаком умножения в виде звёздочки ( ∗ ) он появился в его книге «Teutsche Algebra» в 1659 году. Из-за распространения в Англии знак Рана часто называют «английским знаком деления», но корни его лежат в Германии.

Другие употребления символов ( ÷ ) и ( : )

Символы ( ÷ ) и ( : ) могут использоваться также для обозначения диапазона. Например, «5÷10» может обозначать диапазон [5, 10], то есть от 5 до 10 включительно. Если имеется таблица, строки которой обозначаются числами, а столбцы — латинскими буквами, то запись вида «D4:F11» может использоваться для обозначения массива ячеек (двумерного диапазона) от D до F и от 4 до 11.

Источник статьи: http://dic.academic.ru/dic.nsf/ruwiki/232402

Блог молодого админа

Увлекательный блог увлеченного айтишника

Знак деления на клавиатуре компьютера или ноутбука: как поставить?

Если вы печатаете с помощью клавиатуры своего компьютера или ноутбука математические примеры, то можете все символы набрать на самой клавиатуре. Не верите? В этой статье мы покажем пример со знаком деления. Способов будет несколько. Какой из них использовать, решать вам. Начнем с наиболее простого.

Двоеточие

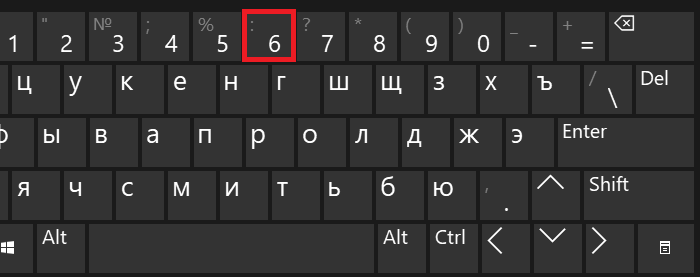
Надо отметить, что знаком деления могут выступать различные символы. Один из них — это двоеточие, находится он на той же клавише, что и цифра 6.

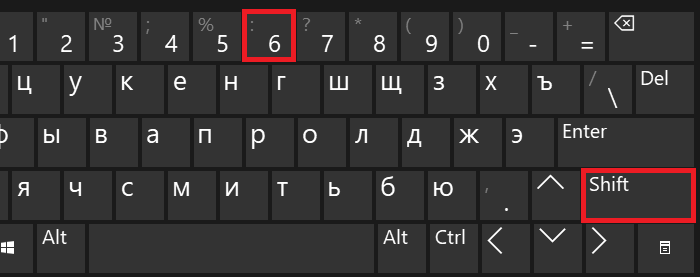
Чтобы поставить этот знак, нужно нажать на Shift и, удерживая клавишу, нажать на клавишу 6, после чего отпустить Shift.

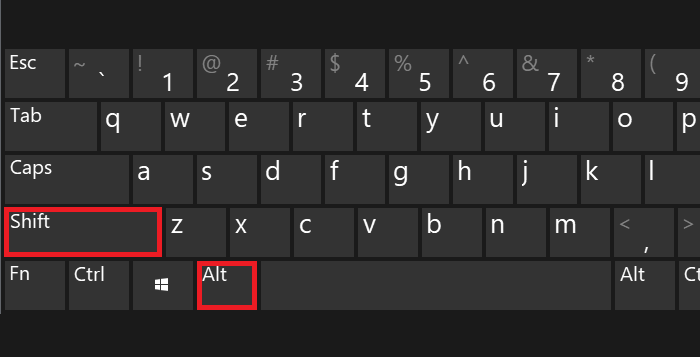
Если вы вдруг увидели другой символ, это говорит о том, что у вас используется англоязычная раскладка. Переключите ее на русскоязычную, нажав на клавиши Shift+Ctrl:

Можете также воспользоваться Alt-кодом. Для этого зажмите Alt и, удерживая его, наберите цифры 58, после чего отпустите Alt.

Если все сделано верно, вы увидите двоеточие.

Если не получилось с правым Alt, используйте левый.

Косая черта

В качестве знака деления может выступать косая черта. Она находится рядом с цифровой клавиатурой.

Просто нажмите на нее один раз.

Что должно получиться:

Раскладка клавиатуры роли не играет.

Alt-код для косой черты — 47:

Символ умножения из таблицы символов

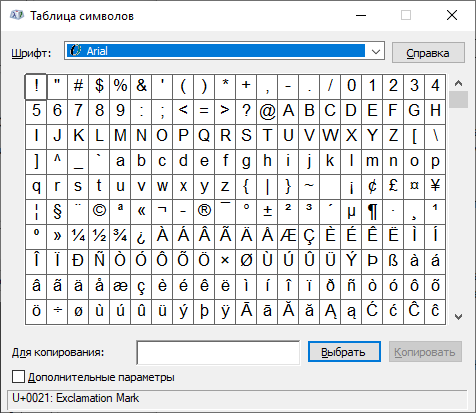
Можете использовать таблицу символов Windows, чтобы указать обелюс (знак деления), который обычно встречается на калькуляторах.

Затем в окно «Выполнить» введите команду charmap.exe и кликните ОК.

Если все сделали верно, увидите таблицу символов Windows.

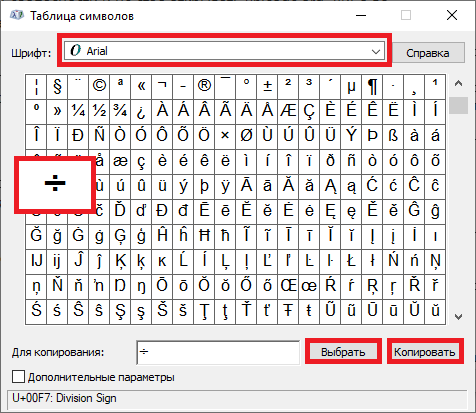
Выбираете шрифт Arial, находите символ деления, кликаете по нему, после чего кликаете по кнопкам «Выбрать» и «Копировать».

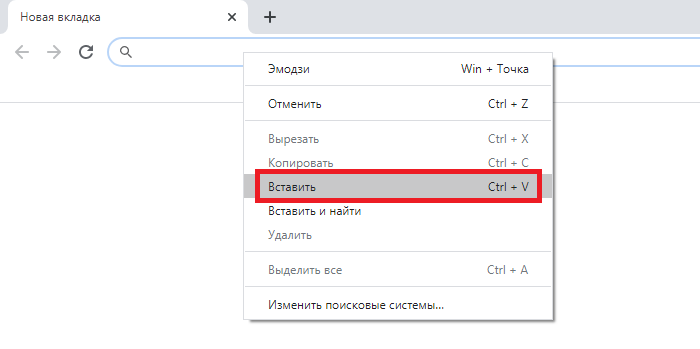
Можно использовать и Alt-коды.

В данном случае нужно набрать цифры 0247 на цифровой клавиатуре (англоязычная раскладка).

Источник статьи: http://fulltienich.com/znak-deleniya-na-klaviature-kompyutera-ili-noutbuka-windows/

Знак деления

Знак деления — математический символ в виде двоеточия ( : ) , обелюса ( ÷ ) или косой черты ( / ) , используемый для обозначения оператора деления.

В большинстве стран предпочитают двоеточие ( : ) , в англоязычных странах и на клавишах микрокалькуляторов — символ ( ÷ ) . Для математических формул во всём мире отдают предпочтение знаку ( / ) .

История символа

Немецкий математик Лейбниц предпочитал двоеточие ( : ) . Этот символ он использовал впервые в 1684 г. в своём труде Acta eruditorum. До Лейбница этот знак был использован англичанином Джонсоном 1633 в одной книге, но как знак дроби, а не деления в узком смысле.

Немецкий математик Йоханн Ран ввёл для обозначения деления знак ( ÷ ) . Вместе со знаком умножения в виде звездочки ( ∗ ) он появился в его книге «Teutsche Algebra» 1659 г. Из-за распространения в Англии знак Рана часто называют «английским знаком деления», но корни его лежат в Германии.

Другие употребления символов ( ÷ ) и ( : )

Символы ( ÷ ) и ( : ) могут использоваться также для обзначения диапазона. Например, «5÷10» может обозначать диапазон [5, 10], то есть от 5 до 10 включительно. Если имеется таблица, строки которой обозначаются числами, а столбцы — латинскими буквами, то запись вида «D4:F11» может использоваться для обозначения массива ячеек (двумерного диапазона) от D до F и от 4 до 11.

Источник статьи: http://vlab.wikia.org/ru/wiki/%D0%97%D0%BD%D0%B0%D0%BA_%D0%B4%D0%B5%D0%BB%D0%B5%D0%BD%D0%B8%D1%8F

Как называется знак решётки? &, #, ÷, *

«Знак решётки», «деление», «вместо and», «звёздочка» , «буква R», «вопрос наоборот» — как правильно называются символы?

ДЕЛЕНИЕ — «ОБЕЛЮС»

От латинского obelus — от греческого ὀβελός. В этих словах тот же корень, что и в слове обелиск.

Именно так — обелюс — называется знак деления. Он напоминает объединение знаков минуса и двоеточия. Был введён древнегреческим филологом, александрийским библиотекарем Зенодотом Эфесским для обозначения сомнительности. Символ мог выглядеть либо как обычная горизонтальная черта, либо как та же черта, но с добавлением точек по одной сверху и снизу. Ставился на полях напротив тех частей текста, которые вызывали сомнения в ходе проверки поступавших в библиотеку рукописей.

В 1659 году немецкий математик Йоханн Ран в своей работе впервые применил обелюс для обозначения деления. Некоторые авторы использовали этот символ как знак вычитания, что стало нормой в некоторых странах Европы — например в Норвегии и Дании. В Польше обелюс использовался для обозначения диапазонов, например, запись 3÷7 означала «от трёх до семи».

РЕШЁТКА — ОКТОТОРП

От латинского octothorpe — восемь концов

Другие названия знака решётки — хеш, решётка, знак номера, диез или шарп (из-за внешнего сходства этих двух символов), знак фунта ( # часто используют в случаях, когда невозможно ввести символ фунта).

В 60-х годах XX века американские инженеры в области телефонии пытались придумать специальное название для этого символа, такие как октоторп, октаторп и октатерп. Однако ни одно из них так и не получило серьёзного распространения: все употребляли устоявшиеся формы hash sign (хеш-знак) или number sign (знак номера, который часто употребляют в английском языке).

Данный символ не был распространён в русской типографике вплоть до конца XX века. Неспециализированное, бытовое распространение знак получил с распространением цифрового набора номеров в телефонах. В языке за ним закрепился термин «знак решётки».

Источник статьи: http://zen.yandex.ru/media/tolk_slov/kak-nazyvaetsia-znak-reshetki——5aa95947610493d45934e7c0

Деление в стоблик

Существуют элементарные вещи, не требующие объяснения. Но даже элементарное забывается, поэтому сегодня мы будем вспоминать деление в столбик.

Для примера разделим число 984 на 8. В любой операции деления есть делимое, делитель и частное. В нашем случае 984 – делимое, 8 – делитель, а результат деления – частное. Итак, будем искать частное от деления 984 на 8. Записываем рядом делимое и делитель, разделяя их уголком.

Теперь, двигаясь слева направо по цифрам делимого, найти в нем наименьшее число, которое больше делителя. Чисел тут три: 9, 98 и 984. Все они больше делителя (8), но наименьшим является 9. Теперь нужно ответить на вопрос: сколько раз наш делитель (8) содержится в числе 9? Один раз. Поэтому под чертой пишем 1– это первая цифра частного, которое мы пытаемся найти.

Теперь умножаем 8 на 1 и получаем 8. Записываем полученный результат под первым числом делимого. Далее вычитаем в столбик, то есть из 9 вычитаем 8 и получаем 1.

Если вы все сделали правильно, результат вычитания должен быть меньше делителя. У нас 1 меньше 8! Если у вас получилось больше, значит вы неправильно определили, сколько раз 8 содержится в 9.

Переходим к следующему этапу деления, для этого нужно увеличить наш результат вычитания. Делают это с помощью следующей цифры делимого. Первую цифру (9) мы уже использовали, значит, берем следующую (8) и приписываем к единице.

И снова отвечаем на знакомый вопрос. Сколько раз 8 содержится в 18? Два раза. Приписываем двойку к единице под чертой — это вторая цифра частного. Умножаем 2 на 8, получаем 16 и записываем результат под 18.

Дальше идем по уже знакомому пути. Вычитаем 16 из 18, получаем 2 (2 меньше 8, значит все сделано правильно). Используем следующую и последнюю цифру делимого – 4, сносим ее вниз и приписываем к двойке, получая 24.

Снова отвечаем на знакомый вопрос. Сколько раз 8 содержится в 24? Три раза. Пишем тройку под чертой. Умножаем 8 на 3, получаем 24 и записываем в столбик под 24. Вычитаем 24 из 24, получаем 0. Деление выполнено без остатка! Ответ – 123.

Если вы использовали все цифры делимого, а ноль так и не получился, значит или деление без остатка невозможно, или вы ошиблись в вычислениях.

Здесь вроде все просто, а как быть в случае, если при ответе на вопрос «Сколько раз делитель содержится в числе?» ответ – нисколько? Рассмотрим второй пример: теперь разделим 808 на 8: результат первого же вычитания равен нулю и приписываем к нулю тоже нуль. В этом случае в ноле восемь не содержится ни разу или нуль раз, значит записываем в результат нуль и сносим следующую цифру 8, а дальше повторяем знакомый алгоритм:

Все рассмотренные выше примеры заканчивались делением нацело, а как быть, если деление без остатка не возможно? В этом случае, когда цифры делимого закончились, в частном ставят десятичную запятую и приписывают к остатку от вычитания нули, продолжая известные действия деления в столбик. Например, при делении числа 804 на 8 приходим к случаю, когда в остатке вычитания нуль и приписанная цифра нуль – в результате записываем нуль и приписываем следующую цифру делимого (4), в которой 8 тоже содержится нуль раз. Снова в результат записываем нуль и ставим десятичную запятую, так как цифры делимого закончились, а приписываем 0. Теперь нужно определить сколько раз 8 содержится в 40. Пять раз. Продолжая деление в столбик, получаем в результате вычитания 0. Деление окончено.

И последний момент – это деление десятичных дробей. Для того, чтобы использовать приведенный алгоритм для деления десятичных дробей, необходимо умножить каждую из них на число 10 в степени, равной наибольшему количеству десятичных знаков после запятой в этих дробях. Например, нужно разделить 2025,255 на 2,5. Наибольшее количество знаков после запятой в делимом и оно равно 3. Значит умножить оба этих числа нужно на 10 в 3 степени, т. е. на 1000. Поэтому в столбик будем делить 2025255 на 2500. А это мы уже умеем.

Источник статьи: http://www.stranamam.ru/post/2531690/