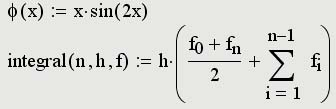Как в маткаде написать функцию

Произвольные зависимости между входными и выходными параметрами задаются при помощи функций. Функции принимают набор параметров и возвращают значение, скалярное или векторное (матричное). В формулах рабочего листа можно использовать стандартные встроенные функции, а также функции, определенные пользователем.

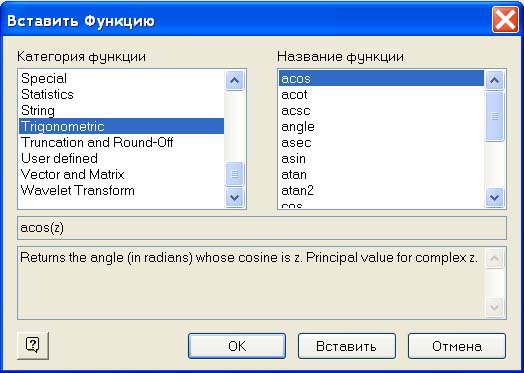
Чтобы использовать функцию в выражении, ее следует вызвать по имени, указав в значения фактических входных параметров в скобках после имени функции. Имена простейших математических функций можно ввести с панели инструментов Калькулятор (Arithmetic). Информацию о других функциях можно почерпнуть в справочной системе или в приложении. Вставить в выражение стандартную функцию можно при помощи команды Вставка > Функция (Insert > Function). В диалоговом окне (рис. 1.9) слева выбирается категория, к которой относится функция, а справа – конкретная функция. В нижней части окна выдается информация о выбранной функции. При вводе функции через это диалоговое окно автоматически добавляются скобки и заполнители для значений параметров.

Пользовательские функции должны быть сначала определены. Определение задается при помощи оператора присваивания. В левой части указывается имя пользовательской функции и, в скобках, формальные параметры – переменные, от которых она зависит. Справа от знака присваивания эти переменные должны использоваться в выражении, например

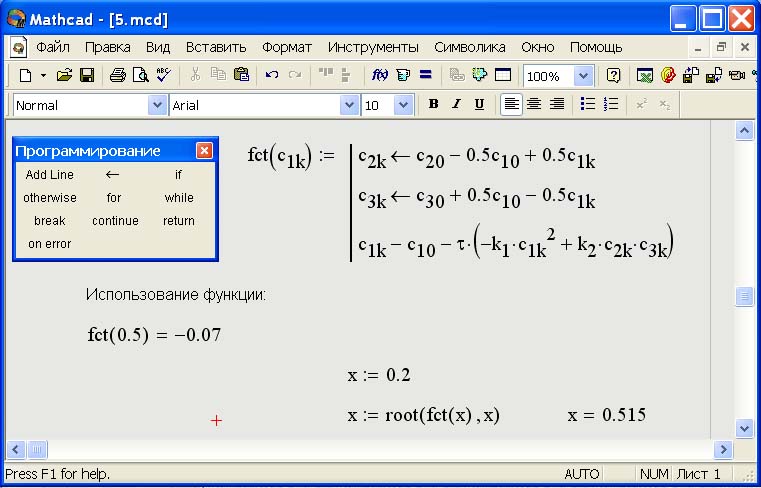
Если для вычисления пользовательской функции необходимо выполнить несколько операций, то в теле функции формируют необходимое число строк с помощью кнопки Add line панели Программирование и в появившиеся заполнители помещают формулы. Отметим, что в операторах тогда допустима операция внутреннего присваивания, задаваемая стрелкой, а все вычисленные подобным образом переменные являются локальными и за пределами функции будут не определенны. Так, на рис. 1.10 функция fct вычисляется за три действия, а переменные с_2k и c_3k будут видимыми только внутри функции.

При применении пользовательской функции в последующих формулах ее имя вводят вручную. В диалоговом окне Вставка функции оно не отображается.

Источник статьи: http://eco.sutd.ru/mathcad/docs/mathcad/functions.htm

Урок 5. Переменные и функции в Mathcad

Возможности Mathcad можно в полной мере оценить только при использовании переменных и функций.

Два знака равенства

В выражениях Вам необходимо использовать числа (константы), переменные, операторы и знаки равенства. В повседневной жизни мы используем знак равенства = для различных операций. Mathcad, однако, различает эти операции. Наиболее важные из них:

определение (присвоить значение) – вводится через двоеточие [:]
вычисление – вводится через знак равенства [=]

Оператор определения не менее важен, чем оператор вычисления. Значение выражения y можно отобразить только после присвоения ему какого-либо значения. x и y здесь являются переменными.

Введите следующие выражения:

Эти два знака равенства принципиально различны, поэтому их не следует путать.

Поместите курсор перед числом 4 в первом выражении:

Удалите число 4 с помощью клавиши [Delete] и введите 5. Щелкните по пустой области и убедитесь, что результат третьего выражения изменился на 25:

Попробуйте удалить число 25. Вы увидите, что при первом нажатии число станет красным, а при повторном нажатии удалится 25 и знак равенства:

Использование переменных

Введите следующие выражения:

Попробуйте изменить значение x на 100, 0.5, -4 и 0:

Первые два случая дадут в результате число. При -4 получится мнимое число. Да, Mathcadможет работать и с такими числами. При нуле программа выдаст ошибку, а результат будет обведен красным. Если Вы щелкните по неправильному выражению, то получите описание, что может быть не так:

Теперь о том, какие имена можно и нельзя использовать для переменных. Есть несколько правил: имя переменной не может начинаться с цифры и в имени переменной нельзя использовать пробелы и знаки операторов. Имена переменных могут начинаться:

с любой строчной или прописной буквы
другие символы, если они не являются операторами
символы с вкладки Математика –> Операторы и символы –> Символы
символы из Таблицы символов Windows

Переменные можно использовать, только если они были определены ранее. «Ранее» означает, что объявление переменной должно располагать выше или левее выражения, где она используется. Если переменная не объявлена, появится сообщение об ошибке:

Подстрочные индексы

В Mathcad есть два различных вида подстрочных индекса для переменных:

Описательный подстрочный индекс.
Индекс массива (матрицы).

Чтобы набрать описательный подстрочный индекс, введите имя переменной, нажмите [Ctrl+-] и наберите подстрочный индекс:

Переменная с описательным подстрочным индексом – это обычная переменная, со своим именем. Индекс массива существенно отличается от него. Этот индекс можно ввести, нажав открывающую квадратную скобку [ после имени переменной. У переменной может быть один или два индекса массива:

Индекс массива должен быть числом. При этом не следует путать виды подстрочных индексов, т.к. они выглядят практически идентично:

Разница видна при щелчке мышью по выражению:

У переменной может быть сразу описательный индекс и индекс массива. Сначала всегда идет описательный индекс:

Функции

Переменные можно использовать, только если они были определены ранее. Однако есть одно важное исключение – определение функции. Можно определить собственную функцию, как на примере ниже:

Переменная a является локальной для функции. Она не определена за пределами функции:

Если Вы определили a до определения функции, значение a не будет изменено в процессе вычисления значения функции.

Внимание: если Вы дали переменной такое же имя, как и функции, Вы больше не сможете использовать эту функцию. У переменной и функции должны быть разные имена:

Этой проблемы можно избежать, задав для переменной и функции разные обозначения. Об этом мы поговорим в уроке 10 «Обозначения и единицы измерения».

Функции могут содержать две и более переменной:

Здесь значения переменных xи yтакже не изменяются при вычислении функции.

Встроенные функции

В Mathcad есть большое число встроенных функций. Зайдите на вкладку Функции:

Список всех функций можно увидеть, щелкнув по кнопке Все функции.

Заметьте, что тригонометрические функции принимаю в качестве аргумента угол в радианах, а не в градусах. Для использования градусов используйте символ с вкладки Математика –> Операторы и символы –> Символы:

Математика в тексте

В текст можно вставить математическую область. Таким образом, можно использовать над- и подстрочные символы в тексте. Для этого при редактировании текстовой области нажмите кнопку Математика с вкладки Математика –> Области:

Источник статьи: http://sapr-journal.ru/uroki-mathcad/urok-5-peremennye-i-funkcii/

Встроенные операторы и функции Mathcad

Таблица ПЗ.1. Арифметические операторы

Вычитание или отрицание (унарная операция)

Матричное умножение, умножение на скаляр

Скобки (изменение приоритета)

Возведение матрицы в степень n

Скалярные операции над векторами и матрицами, если это не оговорено особо, производятся независимо над их каждым элементом, как над скаляром.

Таблица П3.2. Вычислительные операторы

Вычисление n-й производной

Сумма ранжированной переменной

Произведение ранжированной переменной

Таблица ПЗ.З. Встроенные функции по алфавиту

Обратная тригонометрическая или гиперболическая функция *

Функция Эйри первого рода

Угол между точкой и осью ОХ

file— строковое представление пути к файлу

Дозапись данных в существующий текстовый файл

Аргумент комплексного числа

Угол, отсчитываемый от оси ОХ до точки (х,у)

Слияние матриц слева направо

Мнимая и действительная части функции Бесселя —Кельвина

Функция Эйри второго рода

и — вектор значений сшивок В-сплайнов

Вектор коэффициентов В-сплайна

Возвращает матрицу с решением задачи Коши для системы ОДУ методом Булирша-Штера

bulstoer (y0, t0, t1, acc, D, k, s)

Возвращает матрицу с решением задачи Коши для системы ОДУ методом Булирша-Штера (для определения только последней точки интервала)

Bvalf it (z1, z2, x0, x1, xf, D, load1, load2, score)

zl,z2 — вектор начальных значений для недостающих левых и правых граничных условий

хО — левая граница xl — правая граница xf — внутренняя точка

D(x,y) — векторная функция, задающая систему ОДУ

Возвращает вектор недостающих граничных условий у краевой задачи для системы N ОДУ с дополнительным условием в промежуточной точке

loadl (xO , z ) , Ioad2 (xl , z ) -векторные функции, задающие левые и правые граничные условия

score (xf , у ) — векторная функция, задающая сшивку решений в xf

Наименьшее целое, не меньшее х

Вектор прямого комплексного преобразования Фурье (в разных нормировках)

А — квадратная, определенная матрица

Объединение строковых переменных

Числа обусловленности в разных нормах (Ы, L2, Евклидова, »)

А — матрица i — индекс столбца

Сортировка строк матрицы по элементам 1-го столбца

CreateMesh (F, s0, s1, t0, t1, sgr, tgr, fmap)

F ( s , t ) — векторная функция из трех элементов

tO.tl — пределы! sO.sl — пределы s

tgr, sgr — число точек сетки по t и s

fmap— функция преобразования координат

Создание вложенного массива, представляющего х-, у- и z -координаты параметрической поверхности, заданной функцией F

Cre-ateSpace(F[, t0, t1, tgr, fmap])

F(t) — векторная функция из трех элементов

tgr — число точек сетки по t

fmap— функция преобразования координат

Создание вложенного массива, представляющего х-, у- и z -координаты параметрической пространственной кривой, заданной функцией F

Вектор коэффициентов кубического сплайна

r,6,z— цилиндрические координаты

Преобразование цилиндрических координат в прямоугольные

х— значение случайной величины

par — список параметров распределения *

Плотность вероятности со статистикой распределения *

Диагональная матрица, на диагонали которой находятся элементы вектора

Собственные значения матрицы

Собственный вектор матрицы, соответствующий заданному собственному значению

Собственные векторы матрицы

Возвращает строку S как сообщение об ошибке

g — вектор начальных значений а,Ь,с

Вектор прямого преобразования Фурье (в разных нормировках)

а,Ь,с — параметры х — аргумент, -1 0

Функция Бесселя второго рода нулевого, первого и m-го порядка

Сферическая функция Бесселя второго рода

Некоторые функции, составляющие семейства типовых функций, приведены в сокращенном виде с недостающей частью имени в виде звездочки *. Например, различные статистические функции, описывающие различные распределения, или функции вывода в файлы. Подробные сведения содержатся в разделе, на который указывает соответствующая ссылка.

Когда тот или иной физик использует понятие «физический вакуум», он либо не понимает абсурдности этого термина, либо лукавит, являясь скрытым или явным приверженцем релятивистской идеологии.

Понять абсурдность этого понятия легче всего обратившись к истокам его возникновения. Рождено оно было Полем Дираком в 1930-х, когда стало ясно, что отрицание эфира в чистом виде, как это делал великий математик, но посредственный физик Анри Пуанкаре, уже нельзя. Слишком много фактов противоречит этому.

Для защиты релятивизма Поль Дирак ввел афизическое и алогичное понятие отрицательной энергии, а затем и существование «моря» двух компенсирующих друг друга энергий в вакууме — положительной и отрицательной, а также «моря» компенсирующих друг друга частиц — виртуальных (то есть кажущихся) электронов и позитронов в вакууме.

Однако такая постановка является внутренне противоречивой (виртуальные частицы ненаблюдаемы и их по произволу можно считать в одном случае отсутствующими, а в другом — присутствующими) и противоречащей релятивизму (то есть отрицанию эфира, так как при наличии таких частиц в вакууме релятивизм уже просто невозможен). Подробнее читайте в FAQ по эфирной физике.

Источник статьи: http://bourabai.kz/einf/mathcad/a3.htm