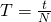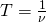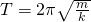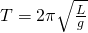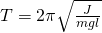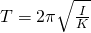ИНФОФИЗ — мой мир.
Весь мир в твоих руках — все будет так, как ты захочешь
Весь мир в твоих руках — все будет так, как ты захочешь
Как сказал.
Информация в чистом виде ‒ это не знание. Настоящий источник знания ‒ это опыт.
Альберт Эйнштейн
Тестирование
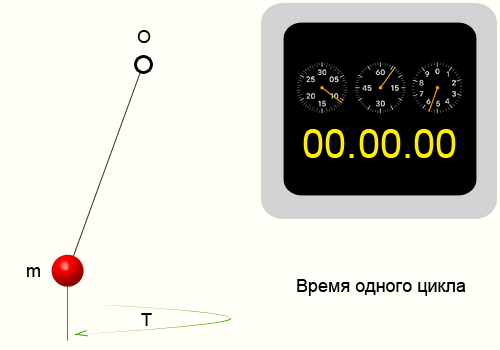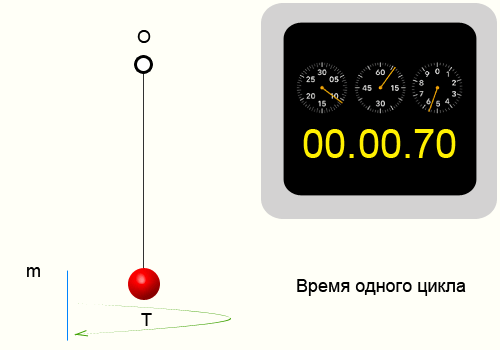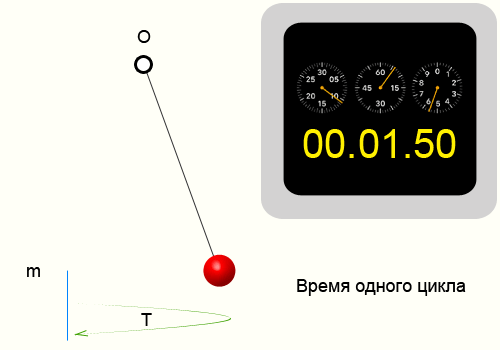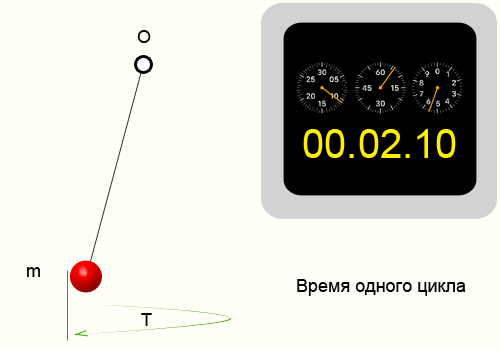
Период колебаний
Период колебаний — минимальный промежуток времени, за который тело совершает одно полное колебание
Для нахождения периода колебаний надо время всех колебаний разделить на количество колебаний:
Период колебаний — величина, обратная частоте колебаний:
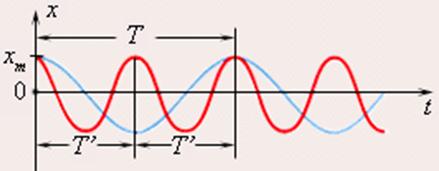
Период колебаний на графике — это расстояние между двумя точками, совершающими волебания в одинаковых фазах:
красная кривая отличается от синей только значением периода (T’ = T / 2)
Период колебаний пружинного маятника 
Период колебаний математического маятника 
Период колебаний физического маятника 
Период колебаний крутильного маятника 
T — период колебаний маятника
N — количество колебаний
t — время, за которое было совершено N колебаний
m — масса груза, или масса маятника
k — жесткость пружины
g — ускорение свободного падения
J — момент инерции маятника относительно оси вращения
l — расстояние от оси вращения до центра масс
I — момент инерции тела
K — вращательный коэффициент жёсткости маятника
Источник статьи: http://infofiz.ru/index.php/mirfiziki/formuly/356-pk
Период и частота колебаний
Период колебаний
Период — это отрезок времени, которое необходимо для совершения одного цикла периодического процесса.
Периодом ($T$) колебаний называют время, за которое совершается одно полное колебание.
За время равное периоду колебаний фаза изменяется на величину равную $2\pi $, поэтому:
Разные периодические процессы, (процессы, повторяющиеся через равные промежутки времени) можно представить в виде совокупности наложенных гармонических колебаний.
Гармонические колебания некоторого параметра $\xi $ описываются уравнением:
где $A=<\xi >_
Формулы для вычисления периода простейших колебательных систем
Период колебаний пружинного маятника определим как:
на упругой пружине, жесткость которой равна $k,$ подвешен груз массой $m$.
Период колебаний математического маятника зависит от ускорения свободного падения ($g$) и длины подвеса ($l$)
Формула для вычисления периода колебаний физического маятника представляет собой выражение:
где $J$ — момент инерции маятника относительно оси вращения; $a$ — расстояние от центра масс тела до оси вращения.
Единицами измерения периода служат единицы времени, например секунды.
Частота колебаний
Физическая величина обратная периоду колебаний называется частотой колебаний ($\nu $).
Частота — это количество полных колебаний, которые колебательная система совершает за единицу времени.
Частота колебаний связана с циклической частотой как:
Единицей измерения частоты в Международной системе единиц (СИ) является герц или обратная секунда:
Примеры задач с решением
Задание. Каковы период ($T$) и частота ($\nu $) колебаний, которые происходят в соответствии с уравнением: $x=A<\sin (<\omega >_0(t+\tau ))\ >$, где $<\omega >_0=2,5\ \pi \ (\frac<рад><с>)$; $\tau =0,4\ $с?
Решение. Из уравнения колебаний:
заключаем, что это гармонические колебания, так как они происходят по закону синуса следовательно, они являются периодическими. Период найдем, зная циклическую частоту колебаний:
Подставляя имеющиеся данные, вычислим период колебаний:
Частоту колебаний найдем как величину, обратную периоду:
Ответ. $T=0,8$ с; $\nu =1,25\ Гц$
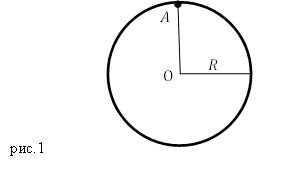
Задание. Какими будут период и частота малых колебаний тонкого обруча, который висит на гвозде (точка А), вбитом горизонтально в стену (рис.1)? Колебания совершаются в плоскости параллельной стене. Радиус обруча R.
Решение. В этой задаче мы имеем дело с физическим маятником период которого, найдем, используя формулу:
Осью вращения обруча является гвоздь, находящийся в точке А. Цент масс обруча находится в его геометрическом центре, точке О, следовательно, расстояние от центра масс до оси вращения обруча (рис.1) равно:
Найдем момент инерции обруча относительно оси, перпендикулярной плоскости обруча, проходящей через точку $A$. Для этого воспользуемся теоремой Штейнера:
где $J_0=mR^2$ — момент инерции обруча, относительно оси, проходящей через его центр (т.О), перпендикулярно плоскости обруча; расстояние между осями равно радиусу обруча. Получаем, момент инерции обруча относительно гвоздя равен:
Используя формулы (2.1) (2.2) и (2.4), имеем:
Отталкиваясь от полученного результата, найдем частоту колебаний как:
Источник статьи: http://www.webmath.ru/poleznoe/fizika/fizika_115_period_i_chastota_kolebanij.php
Период колебаний, формула
Повторяющиеся движения или процессы, которые воспроизводят все состояния предыдущего цикла являются периодическими. Одной из характеристик периодических процессов или колебаний является период.
Период колебаний — Это время за которое периодический процесс проходит полностью один цикл.
Для того чтобы найти период колебаний, необходимо взять определенный временной интервал и подсчитать количество циклов, после чего воспользоваться формулой:
| ∆t | определенный временной интервал, | секунд |
|---|---|---|
| N | количество циклов, | шт. |
| f | частота колебаний (число циклов в одну секунду), | Герц |
Пример определения периода колебаний
Например возьмем кусочек пластилина и подвесим его на нитке. Отведем нитку от положения равновесия и отпустим. На сотовом телефоне в момент отпускания запустим секундомер. Отсчитаем 10 циклов, т.е. нить 10 раз вернется в ту же точку из которой мы ее отпустили. Секундомер показал 14.35 секунд, соответственно приблизительный период колебаний нити 1.435 секунд.
Как в физике пишется период
Представление о периодах колебаний различных физических процессов дает статья Частотные интервалы (учитывая то, что период в секундах есть обратная величина частоты в герцах).
Некоторое представление о величинах периодов различных физических процессов также может дать шкала частот элетромагнитных колебаний (см. Электромагнитный спектр) .
Периоды колебаний слышимого человеком звука находятся в диапазоне
(четкие границы его несколько условны).
Периоды электромагнитных колебаний, соответствующих разным цветам видимого света — в диапазоне
от 1,1·10 -15 с до 2,3·10 -15 с.
Поскольку при экстремально больших и экстремально маленьких периодах колебаний методы измерения имеют тенденцию становятся всё более косвенными (вплоть до плавного перетекая в теоретические экстраполяции), трудно назвать четкую верхнюю и нижнюю границы для периода колебаний, измеренного непосредственно. Какую-то оценку для верхней границы может дать время существования современной науки (сотни лет), а для нижней — период колебаний волновой функции самой тяжелой из известных сейчас частиц ().
В любом случае границей снизу может служить планковское время, которое столь мало, что по современным представлениям не только вряд ли может быть вообще как-то физически измерено [4] , но и вряд ли в более-менее обозримом будущем представляется возможность приблизиться к измерению величин даже на много порядков меньших. а границей сверху — время существования Вселенной — более десяти миллиардов лет.
Периоды колебаний простейших физических систем
Пружинный маятник
Период колебаний пружинного маятника может быть вычислен по следующей формуле:
,
где 
— масса груза, 
— жёсткость пружины.
Математический маятник
где 
— длина подвеса (к примеру нити), 
— ускорение свободного падения.
Период колебаний (на Земле) математического маятника длиной 1 метр с хорошей точностью [5] равен 2 секундам.
Физический маятник
где 
— момент инерции маятника относительно оси вращения, — масса маятника, — расстояние от оси вращения до центра масс.
Крутильный маятник
где 
— момент инерции тела, а 
— вращательный коэффициент жёсткости маятника.
Электрический колебательный (LC) контур
Период колебаний электрического колебательного контура:
,
где 
— индуктивность катушки, 
— ёмкость конденсатора.
Эту формулу вывел в 1853 году английский физик У. Томсон.
Примечания
- ↑ Состояние механической системы характеризуется положениями и скоростями всех ее материальных точек (строже говоря — координатами и скоростями, соответствующими всем степеням свободы данной системы), для немеханической — их формальными аналогами (которые также можно назвать координатами и скоростями в смысле абстрактного описания динамической системы — в количестве, также равном количеству ее степеней свободы).
- ↑ Для монохроматических волн это уточнение самоочевидно, для близких к монохроматическим — интуитивно очевидно по аналогии со строго монохроматическими, для существенно немонохроматических — наиболее ясный случай сводится к тому, что фазовые скорости всех монохроматических компонент совпадают друг с другом, поэтому комментируемое утверждение ьакже верно.
- ↑ С точностью до единиц измерения: в традиционных (обычных) системах физических единиц частота и энергия измеряются в разных единицах (поскольку до появления квантовой теории совпадение энергии и частоты было неизвестно, и, естественно, для каждой из величин была выбрана своя независимая единица измерения), поэтому при измерении их в обычных (разных) единицах, например, джоулях и герцах требуется переводной коэффициент (так называемая константа Планка). Однако можно выбрать систему единиц измерения так, чтобы в ней константа Планка стала равной 1 и пропала из формул; в такой системе единиц энергия любой частицы просто равна частоте колебания ее волновой функции (а значит обрата периоду этого колебания).
- ↑ Имеется в виду, конечно же, невозможность экспериментального измерения времен конкретных процессов или периодов колебаний такого порядка, а не просто вычисление некоторого числа.
- ↑ Лучше, чем 0,5%, если взять метрологическое или принятое техническое значение ускорения свободного падения; И с разбросом
0.53% для максимального и минимального значений ускорения свободного падения, наблюдаемых на земле.
Ссылки
- Проставив сноски, внести более точные указания на источники.
- Добавить иллюстрации.
Wikimedia Foundation . 2010 .
Смотреть что такое «Период колебаний» в других словарях:
период колебаний — период Наименьший промежуток времени, через который повторяется состояние механической системы, характеризуемое значениями обобщенных координат и их производных. [Сборник рекомендуемых терминов. Выпуск 106. Механические колебания. Академия наук… … Справочник технического переводчика
Период (колебаний) — ПЕРИОД колебаний, наименьший промежуток времени, через который совершающая колебания система возвращается в то же состояние, в котором она находилась в начальный момент, выбранный произвольно. Период величина, обратная частоте колебаний. Понятие… … Иллюстрированный энциклопедический словарь
ПЕРИОД КОЛЕБАНИЙ — наименьший промежуток времени, через к рый .система, совершающая колебания, снова возвращается в то же состояние, в к ром она находилась в нач. момент, выбранный произвольно. Строго говоря, понятие «П. к.» применимо лишь, когда значения к. л.… … Физическая энциклопедия
ПЕРИОД КОЛЕБАНИЙ — наименьший промежуток времени, через который колеблющаяся система возвращается к исходному состоянию. Период колебаний величина, обратная частоте колебаний … Большой Энциклопедический словарь
период колебаний — период колебаний; период Наименьший промежуток времени, через который повторяется состояние механической системы, характеризуемое значениями обобщенных координат и их производных … Политехнический терминологический толковый словарь
Период колебаний — 16. Период колебаний Наименьший интервал времени, через который при периодических колебаниях повторяется каждое значение колеблющейся величины Источник … Словарь-справочник терминов нормативно-технической документации
период колебаний — наименьший промежуток времени, через который колеблющаяся система возвращается к исходному состоянию. Период колебаний величина, обратная частоте колебаний. * * * ПЕРИОД КОЛЕБАНИЙ ПЕРИОД КОЛЕБАНИЙ, наименьший промежуток времени, через который… … Энциклопедический словарь
период колебаний — virpesių periodas statusas T sritis automatika atitikmenys: angl. oscillation period; period of oscillations; period of vibrations vok. Schwingungsdauer, m; Schwingungsperiode, f; Schwingungszeit, f rus. период колебаний, m pranc. période d… … Automatikos terminų žodynas
период колебаний — virpesių periodas statusas T sritis Standartizacija ir metrologija apibrėžtis Mažiausias laiko tarpas, po kurio pasikartoja periodiškai kintančių dydžių vertės. atitikmenys: angl. vibration period vok. Schwingungsdauer, f; Schwingungsperiode, f… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
период колебаний — virpesių periodas statusas T sritis chemija apibrėžtis Mažiausias laiko tarpas, po kurio pasikartoja periodiškai kintančių dydžių vertės. atitikmenys: angl. period of oscillation; period of vibration; vibration period rus. период колебаний … Chemijos terminų aiškinamasis žodynas
Источник статьи: http://dic.academic.ru/dic.nsf/ruwiki/81727