Как правильно пишется слово танграм
Танграм, возможно, ведёт своё происхождение от яньцзиту (燕几圖) — вида мебели, появившегося во времена империи Сун. Как мебель яньцзиту претерпела некоторые изменения за время правления династии Мин, а в дальнейшем превратилась в набор деревянных фигурок для игры.
Хотя танграм часто считают изобретением глубокой древности, первое печатное упоминание о нём встречается в китайской книге, изданной в 1813 году и написанной, очевидно, в правление императора Цзяцина. [1]
Появление танграма на западе относят не ранее чем к началу XIX столетия, когда эти головоломки попали в Америку на китайских и американских судах. Старейший такой экземпляр, подаренный сыну американского судовладельца в 1802 году, сделан из слоновой кости и хранится в шёлковом футляре. [источник не указан 915 дней]
Слово «танграм» впервые было использовано в 1848 году Томасом Хиллом, в дальнейшем президентом Гарвардского университета, в его брошюре «Головоломки для обучения геометрии».
Писатель и математик Льюис Кэрролл считается энтузиастом танграма. У него хранилась китайская книга с 323 задачами.
У Наполеона во время его изгнания на остров Святой Елены был набор для танграма и книга, содержащая задачи и решения. Фотографии этого набора содержатся в книге Джерри Слокума The Tangram Book. [2]
Книга Сэма Лойда «Восьмая книга Тан» (англ. The Eighth Book Of Tan ), вышедшая в 1903 году, содержит вымышленную историю танграма, согласно которой эта головоломка была изобретена 4 тысячи лет назад божеством по имени Тан. Книга включает 700 задач, некоторые из которых неразрешимы. [3]
Парадоксы
Парадокс танграма заключается в следующем: каждый раз полностью используя весь набор, можно сложить две фигуры, одна из которых будет подмножеством другой. [4] Один такой случай приписывается Дьюдени: две похожие фигуры изображают монахов, но у одной из них при этом есть нога, а у другой фигуры её нет. [5] Разрешение этого парадокса приводится во многих источниках, в том числе по ссылке. [4]
Другой парадокс предлагается Лойдом в «Восьмой книге Тан»:
Седьмая и восьмая фигуры изображают загадочный квадрат, составленный из семи частей. Затем угол квадрата срезали, но при этом всё равно используются те же семь частей. [6]
The seventh and eighth figures represent the mysterious square, built with seven pieces: then with a corner clipped off, and still the same seven pieces employed.
Решение данного парадокса не приводится в книге Лойда. Другие неразрешённые задачи из этой книги обсуждаются по ссылке. [7]
Подсчёт конфигураций
Ван Футрайн и Сюн Цюаньчжи (熊全治) доказали в 1942 году, что существуют только пятнадцать выпуклых конфигураций танграма (таких, что отрезок прямой, проведённый между любыми двумя точками внешнего контура, пройдёт только через точки, заключённые внутри этого контура; иными словами — без пустот посередине). [8] [9] [10]
Книга Рональда Рида «Танграм: 330 задач» (англ. Tangrams: 330 Puzzles ) просит читателей присылать любые другие фигуры. Такое условие создаёт множество хотя и с гораздо большим числом элементов, чем множество выпуклых фигур, но всё же конечное. [11]
В ответ было предложено приблизительно 6,13 миллиона возможных конфигураций, [12] в каждой из которых при этом хотя бы одна вершина и хотя бы одна сторона любой части совпадают с вершиной и стороной другой части.
Фигуры
Размеры приведены относительно большого квадрата, стороны и площадь которого принимают равными 
- 5 прямоугольных треугольников
- 2 маленьких (с гипотенузой, равной
и катетами
)
- 1 средний (гипотенуза
и катеты
)
- 2 больших (гипотенуза
и катеты
)
- 2 маленьких (с гипотенузой, равной
- 1 квадрат (со стороной
)
- 1 параллелограмм (со сторонами
и
и углами
и
)
Среди этих семи частей параллелограмм выделяется отсутствием у него зеркальной симметрии (он обладает только вращательной симметрией), так что его зеркальное отражение можно получить, только перевернув его. Это единственная часть танграма, которую требуется перевернуть, чтобы сложить определённые фигуры. При использовании одностороннего набора (в котором переворачивать фигуры запрещено) есть фигуры, которые можно сложить, в то время как их зеркальное отражение — нельзя.
Педагогическое значение танграма
Способствует развитию у детей умения играть по правилам и выполнять инструкции, наглядно-образного мышления, воображения, внимания, понимания цвета, величины и формы, восприятия, комбинаторных способностей.
См. также
Примечания
- ↑Chen, Zhongying Advances in computational mathematics: proceedings of the Guangzhou international symposium. — New York, N.Y: Marcel Dekker, 1999. — P. 466. — ISBN 0-8247-1946-8
- ↑Jerry Slocum, Dieter Gebhardt, Jack Botermans, Monica Ma, Xiaohe Ma The Tangram Book. — Sterling Publishing Company, 2003. — ISBN 1-4027-0413-5
- ↑Costello, Matthew J. The Greatest Puzzles of All Time. — New York: Dover Publications, 1996. — ISBN 0-486-29225-8
- ↑ 12Tangram Paradox, by Barile, Margherita, From MathWorld — A Wolfram Web Resource, created by Eric W. Weisstein.
- ↑Dudeney, H. Amusements in Mathematics. — New York: Dover Publications, 1958.
- ↑Loyd, Sam The eighth book of Tan — 700 Tangrams by Sam Loyd with an introduction and solutions by Peter Van Note. — New York: Dover Publications, 1968. — P. 25.
- ↑Unsolved Patterns by Sam Loyd, by Cocchini, Franco, From Tanzzle.com
- ↑ (November 1942) «A Theorem on the Tangram». The American Mathematical Monthly49 (9): 596–599. DOI:10.2307/2303340. Проверено 2009-02-06.
- ↑Read, Ronald C. Tangrams : 330 Puzzles. — New York: Dover Publications, 1965. — P. 53. — ISBN 0-486-21483-4
- ↑А. Панов,Загадка фигуры № 51 // Квант. — 1982. — № 12. — С. 34-37.
- ↑Read, Ronald C. Tangrams : 330 Puzzles. — New York: Dover Publications, 1965. — P. 55. — ISBN 0-486-21483-4
- ↑ Cocchini, F. Ten Millions of Tangram Patterns. TangMath.
- ↑ «Tangram» by Enrique Zeleny, Wolfram Demonstrations Project
Ссылки
Wikimedia Foundation . 2010 .
Смотреть что такое «Танграм» в других словарях:
7 (число) — Запрос «Семь» перенаправляется сюда; см. также другие значения. 7 семь 4 · 5 · 6 · 7 · 8 · 9 · 10 Факторизация: Простое Римская запись: VII Двоичное: 111 Восьмеричное: 7 Шестнадцатерич … Википедия
Головоломка — Для информации об игровом жанре см. Головоломка (жанр компьютерных игр) Головоломка непростая задача, для решения которой, как правило, требуется сообразительность, а не специальные знания высокого уровня. Тем не менее, некоторые… … Википедия
Иноуэ, Кикуко — Кикуко Иноуэ 井上 喜久子 Имя при рождении: 井之上 喜久子 Дата рождения: 25 сентября 1964(1964 09 25) (48 лет) Место рождения … Википедия
Сараев, Андрей — В Википедии есть статьи о других людях с такой фамилией, см. Сараев. В этой биографической статье о человеке из России или страны СНГ не указано отчество. Вы … Википедия
Кубики сома — 7 составных частей куба Сома … Википедия
Поперечная флейта — Классификация • Духовой инструмент • Деревянный духовой инструмент • Лабиальный и … Википедия
Сараев, Андрей Валентинович — В Википедии есть статьи о других людях с такой фамилией, см. Сараев. В этой биографической статье о человеке из России или страны СНГ не указано отчество. Вы … Википедия
Циммерман, Маттиас (художник) — Эта статья предлагается к удалению. Пояснение причин и соответствующее обсуждение вы можете найти на странице Википедия:К удалению/11 июля 2012. Пока процесс обсуждения … Википедия
Pension Kahlua Milk — (Shinano,Япония) Категория отеля: 3 звездочный отель Адрес: 389 1302 Нагано, Shi … Каталог отелей
Источник статьи: http://dic.academic.ru/dic.nsf/ruwiki/440600
Как правильно пишется слово танграм
До появления компьютерных игр и бурного развития настольных, одним из основных развлечений для большинства детей и множества взрослых была игра — головоломка «Танграм «. Базовым элементом танграма являются таны, которые получают при разрезании квадрата на семь геометрических фигур. Из них можно сложить большое количество различных фигур (животные, птицы, орудия труда, мебель, предметы быта и т.д.). Игра помогает развивать логическое мышление, геометрическую интуицию.
Вероятно, что слово «танграм» произошло от слова «Тань” (что означает «китаец”) и корня «грамма” (в переводе с греческого «буква”).
Буквально слово танграм означает «семь дощечек мастерства» . Это головоломка, состоящая из семи плоских фигур, которые складывают определённым образом для получения другой, более сложной, фигуры (изображающей человека, животное, предмет домашнего обихода, букву или цифру и т. д.).
В Китае название “Танграм” неизвестно, а игра имеет название «ЧИ-ЧАО-ТЮ», что в переводе «Хитроумный узор из семи частей», а термин «Танграм» впервые был использован 1848 году Томасом Хиллом, в будущем президентом Гарвардского университета, в брошюре «Головоломки для обучения геометрии».
История появления танграма
“В записках покойного профессора Челленора, попавших в руки автора, — утверждал Лойд, — имеются сведения о том, что семь книг о танграмах, каждая из которых насчитывает ровно тысячу фигур, были составлены в Китае более 4000 лет назад.
Согласно легенде Лойда, Тан был легендарным китайским мудрецом, которому его соотечественники поклонялись как божеству. Фигуры в своих семи книгах он расположил в соответствии с семью стадиями в эволюции Земли. Его танграмы начинаются с символических изображений хаоса и принципа “инь и ян”. Затем следуют простейшие формы жизни, по мере продвижения по древу эволюции появляются фигуры рыб, птиц, животных и человека. По пути в различных местах попадаются изображения того, что создано человеком: орудию труда, мебель, одежда и архитектурные сооружения.
более 4000 тысяч лет назад у строителя из рук выпала фарфоровая плитка и разбилась на семь частей. Он в спешке, расстроенный, старался сложить ее, но каждый раз получал не квадрат. Это занятие оказалось настолько увлекательным, что впоследствии квадрат, составленный из семи геометрических фигур, назвали Доской Мудрости.
Около 2,5-ой тысяч лет тому назад у немолодого императора Китая родился долгожданный сын и наследник. Шли годы. Мальчик рос здоровым и сообразительным не по годам, но не хотел учиться. Мальчик играл только игрушками, познания наук его не интересовали. Поэтому император позвал к себе трех мудрецов, которые были художником, математиком и философом. Император велел им придумать игру, играя в которую, наследник изучил начала математики, научился смотреть на мир пристальными глазами художника и стал бы терпеливым, как истинный философ, При этом понял, что зачастую сложные вещи состоят из простых вещей. Подумав некоторое время, три мудреца представили императору игру «Ши-Чао-Тю»- квадрат, разрезанный на семь частей.
Появление на западе относят к началу XIX века, когда в 1802 году китайцы подарили сыну американского судовладельца танграм из слоновой кости в шелком футляре.
Упоминание танграма в литературе
Правила игры
1. В каждую собранную фигуру должны входить все семь элементов.
2. При составлении фигур элементы не должны налегать друг на друга.
3. Элементы фигур должны примыкать один к другому.
Парадоксы Танграм
Парадокс танграма заключается в следующем: каждый раз полностью используя весь набор, можно сложить две фигуры, одна из которых будет подмножеством другой. Один такой случай приписывается Дьюдни: две похожие фигуры изображают монахов, но у одной из них при этом есть нога, а у другой фигуры её нет. Разрешение этого парадокса приводится во многих источниках.
Другой парадокс предлагается Лойдом в «Восьмой книге Тан»:
Источник статьи: http://www.sites.google.com/site/tch5464/eto-nado-znat/nagladnaa-geometria/tangram

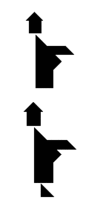



 и катетами
и катетами  )
) и катеты
и катеты  и
и  )
)










