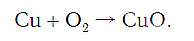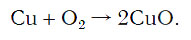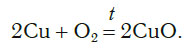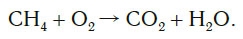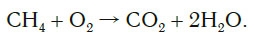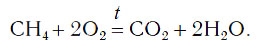Как правильно пишется, ударение в слове «уравнение»
Делаем Карту слов лучше вместе

Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.
Насколько понятно значение слова потряхивать (глагол), потряхивая:
Ассоциации к слову «уравнение»
Синонимы к слову «уравнение»
Предложения со словом «уравнение»
- Сила тяготения, к примеру, нелинейна – этот технический термин означает, в сущности, что вы не можете решать уравнения движения при помощи красивых формул.
Цитаты из русской классики со словом «уравнение»
Сочетаемость слова «уравнение»
Каким бывает «уравнение»
Значение слова «уравнение»
УРАВНЕ́НИЕ , -я, ср. 1. Действие по знач. глаг. уравнять и состояние по знач. глаг. уравняться. (Малый академический словарь, МАС)
Отправить комментарий
Дополнительно
Значение слова «уравнение»
УРАВНЕ́НИЕ , -я, ср. 1. Действие по знач. глаг. уравнять и состояние по знач. глаг. уравняться.
Предложения со словом «уравнение»
Сила тяготения, к примеру, нелинейна – этот технический термин означает, в сущности, что вы не можете решать уравнения движения при помощи красивых формул.
В итоге начинается решение дифференциальных уравнений гуманитарным способом или сочинение диалогов на языке программирования высокого уровня, а в тяжёлых случаях всё сразу и одновременно.
Второй этап состоит из собственно решения уравнения регрессии и нахождения его параметров.
«В уравнение» или «в уравнении», как правильно?
«В уравнении» правильно пишется с буквой «и» в окончании предложного падежа. Слово «в уравнение» имеет окончание «е» как форма винительного падежа с предлогом.
Определим, как различать слова «в уравнении» или «в уравнение» по их грамматическим признакам в контексте.
Слова «в уравнение» и «в уравнении» — это падежные формы существительного среднего рода «уравнение». Они имеют один и тот же предлог «в» и звучат одинаково из-за безударного окончания:
- в у равн е́ни е — приставка/корень/суффикс/окончание;
- в у равн е́ни и — приставка/корень/суффикс/окончание.
Чтобы правильно выбрать окончание, обозначенное буквой «е» или «и», определим падежную форму существительного в контексте.
Когда пишется «в уравнение»?
Когда пишется «в уравнение», выясним, если зададим к нему падежный вопрос в предложении:
Вам следует вставить в уравнение неизвестные величины, обозначенные x и y.
Следует вставить (во что?) в уравнение
Рассматриваемое слово имеет форму винительного падежа единственного числа. Как неодушевленное существительное, оно в винительном падеже имеет такое же безударное окончание, как и форме именительного падежа:
(что?) уравне́ни е — (во что?) в уравне́ни е .
Правописание слова «в уравнении»
Чтобы выяснить, почему «в уравнении» пишется окончание «и», укажем, что предлог «в» может использоваться также в форме предложного падежа существительных:
- поставить ударение (в чём?) в сло́в е
- выросло (в чём?) в по́л е
- заметил (в чём?) в окн е́ .
Как видим, в этой падежной форме существительные среднего рода имеют типичное окончание -е, кроме слов, заканчивающихся буквосочетанием -ие. Такие слова склоняются по-особому. В форме предложного падежа с любым предлогом существительные с конечным сочетанием -ие имеют безударное окончание -и :
- созвезд ие — увидим (в чём?) в созве́зди и
- описан ие — узнаешь (при чём?) при описа́ни и
- расстоян ие — поставьте (на чём?) на расстоя́ни и
- измерен ие — расскажете (о чём?) об измере́ни и .
Обратим внимание, что существительное среднего рода «уравнение» также заканчивается буквосочетанием -ие. Посмотрим, как оно изменяется по падежам в единственном числе:
- и. п. (что?) уравне́ни е
- р. п. формула (чего?) уравне́ни я
- д. п. добавлю (к чему?) к уравне́ни ю
- в. п. напишу (что?) уравне́ни е
- т. п. занят (чем?) уравне́ни е м
- п. п. найдем (в чём?) в уравне́ни и
Поупражняемся в определении падежных форм слова «уравнение» и написании окончаний -е или -и.
Примеры
В уравнение с неизвестными величинами подставьте их значения.
Запишите символы величин, входящих в уравнение.
При решении учтите, что в уравнении не проставлены все коэффициенты.
Ученый внес изменения в уравнение, по-своему понимая физику твердого тела.
В уравнении имеется ошибка, которую вам предстоит указать.
Источник статьи: http://russkiiyazyk.ru/orfografiya/pravopisanie/v-uravnenie-ili-v-uravnenii-kak-pravilno.html
Как правильно написать уравнение
Составить уравнение — значит выразить в математической форме связь между данными (известными) задачи и искомыми (неизвестными) ее величинами. Иногда эта связь, настолько явно содержится в формулировке задачи, что составление уравнения есть просто дословный пересказ задачи, на языке математических знаков.
Пример 1
Петров получил за работу на 160 руб. больше, чем половина суммы, которую получил Иванов. Вместе они получили 1120 руб. Сколько получили за работу Петров и Иванов?
Обозначим через х заработок Иванова. Половина его заработка есть 0,5x ; месячной заработок Петрова 0,5x + 160 вместе они зарабатывают 1120 руб.; математическая запись последней фразы будет
Уравнение составлено. Решая его по раз установленным правилам, находим, заработок Иванова х = 640руб.; заработок же Петрова 0,5x + 160 = 480 (руб.).
Чаще, однако, случается, что связь между данными и искомыми величинами не указывается в задаче прямо; ее нужно установить, исходя из условий задачи. В практических задачах так и бывает почти всегда. Только что приведенный пример носит надуманный характер; в жизни почти никогда подобных задач не встречается.
Для составления уравнения поэтому нельзя дать вполне исчерпывающих указаний. Однако на первых порах полезно руководствоваться следующим. Примем за значение искомой величины (или нескольких величин) какое-нибудь наугад взятое число (или несколько чисел) и поставим себе задачу проверить, угадали ли мы правильное решение задачи или нет. Если мы сумели провести эту проверку и обнаружить либо то, что догадка наша верна, либо то, что она неверна (скорее всего случится, конечно, второе), то мы немедленно можем составить нужное уравнение (или несколько уравнений). Именно, запишем те самые действия, которые мы производили для проверки, только вместо наугад взятого числа введем буквенной знак неизвестной величины. Мы получим требуемое уравнение.
Пример 1
Кусок сплава меди и цинка объемом в 1 дм 3 весит 8,14 кг. Сколько меди содержится в сплаве? (уд. вес меди 8,9 кг/дм 3 ; цинка — 7,0 кг/дм 3 ).
Возьмем наугад число, выражающее искомый объем меди, например 0,3 дм 3 . Проверим, удачно ли мы взяли это число. Так как 1 кг/дм 3 меди весит 8,9 кг, то 0,3 дм 3 весят 8,9 * 0,3 = 2,67 (кг). Объем цинка в сплаве есть 1 — 0,3 = 0,7 (дм 3 ). Вес его 7,0 * 0,7 = 4,9 (кг). Общий вес цинка и меди 2,67+ +4,9 = 7,57 (кг). Между тем вес нашего куска, по условию задачи, 8,14 кг. Догадка наша несостоятельна. Но зато мы немедленно получим уравнение решение которого даст правильный ответ. Вместо наугад взятого числа 0,3 дм 3 обозначим объем меди (в дм 3 ) через х. Вместо произведения 8,9 * 0,3 = 2,67 берем произведшие 8,9 x. Это — вес меди в сплаве. Вместо 1 – 0,3 = 0,7 берем 1 — х; это — объем цинка. Вместо 7,0 * 0,7 = 4,9 берем 7,0 (1 — x); это — вес цинка. Вместо 2,67 + 4,9 берем 8,9х + 7,0 (1 — х); это — общий вес цинка и меди. По условию он равен 8,14 кг; значит, 8,9х +7,0 (1 — x) = 8,14.
Решение этого уравнения дает x = 0,6. Проверку наугад взятого решения можно делать различными способами; соответственно этому можно получить для одной и той же задачи различные виды уравнения; все они, однако, дадут для искомой величины одно и, то же решение, такие уравнения называются равносильными друг другу.
Разумеется, после получения навыков в составлении уравнений нет нужды производить проверку наугад взятого числа: можно для значения искомой величины брать не число, а какую-нибудь букву (х, у и т. д.) и поступать так, как если бы эта буква (неизвестное) была тем числом, проверить которое мы собираемся.
Источник статьи: http://www.maths.yfa1.ru/algebra.php?id=16
Урок 12. Составление уравнений химических реакций
В уроке 12 «Составление уравнений химических реакций» из курса «Химия для чайников» мы научимся составлять уравнения химических реакций и правильно расставлять в них коэффициенты.
Составлять химические уравнения и производить расчеты по ним нужно, опираясь на закон сохранения массы веществ при химических реакциях. Рассмотрим, как можно составить химическое уравнение, на примере реакции меди с кислородом.
Слева запишем названия исходных веществ, справа — продуктов реакции. Если веществ два и более, соединяем их знаком «+». Между левой и правой частями пока поставим стрелку:
медь + кислород → соединение меди с кислородом.
Подобное выражение называют схемой химической реакции. Запишем эту схему при помощи химических формул:
Число атомов кислорода в левой части схемы равно двум, а в правой — одному. Так как при химических реакциях атомы не исчезают, а происходит только их перегруппировка, то число атомов каждого элемента до реакции и после реакции должно быть одинаковым. Чтобы уравнять число атомов кислорода в левой и правой частях схемы, перед формулой CuO ставим коэффициент 2:
Теперь число атомов меди после реакции (в правой части схемы) равно двум, а до реакции (в левой части схемы) — только одному, поэтому перед формулой меди Cu так же поставим коэффициент 2. В результате произведенных действий число атомов каждого вида в левой и правой частях схемы одинаково, что дает нам основание заменить стрелку на знак «=» (равно). Схема превратилась в уравнение химической реакции:
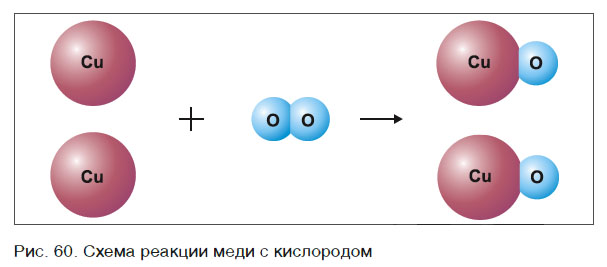
Это уравнение читается так: два купрум плюс о-два равно два купрум-о (рис. 60).
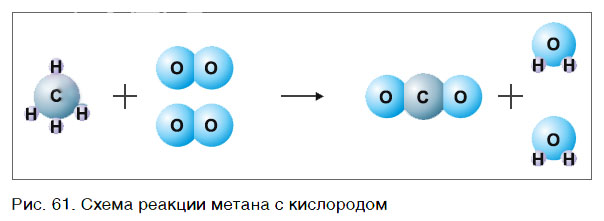
Рассмотрим еще один пример химической реакции между веществами СН4 (метан) и кислородом. Составим схему реакции, в которой слева запишем формулы метана и кислорода, а справа — формулы продуктов реакции — воды и соединения углерода с кислородом (углекислый газ):
Обратите внимание, что в левой части схемы число атомов углерода равно их числу в правой части. Поэтому уравнивать нужно числа атомов водорода и кислорода. Чтобы уравнять число атомов водорода, поставим перед формулой воды коэффициент 2:
Теперь число атомов водорода справа стало 2×2=4 и слева — также четыре. Далее посчитаем число атомов кислорода в правой части схемы: два атома кислорода в молекуле углекислого газа (1×2=2) и два атома кислорода в двух молекулах воды (2×1=2), суммарно 2+2=4. В левой части схемы кислорода только два атома в молекуле кислорода. Для того чтобы уравнять число атомов кислорода, поставим коэффициент 2 перед формулой кислорода:
В результате проведенных действий число атомов всех химических элементов до реакции равно их числу после реакции. Уравнение составлено. Читается оно так: це-аш-четыре плюс два о-два равно це-о-два плюс два аш-два-о (рис. 61).
Данный способ расстановки коэффициентов называют методом подбора.
В химии существуют и другие методы уравнивания чисел атомов элементов в левой и правой частях уравнений реакций, с которыми мы познакомимся позднее.
Краткие выводы урока:
Для составления уравнений химических реакций необходимо соблюдать следующий порядок действий.
- Установить состав исходных веществ и продуктов реакции.
- Записать формулы исходных веществ слева, продуктов реакции — справа.
- Между левой и правой частями уравнения сначала поставить стрелку.
- Расставить коэффициенты, т. е. уравнять числа атомов каждого химического элемента до и после реакции.
- Связать левую и правую части уравнения знаком «=» (равно).
Надеюсь урок 12 «Составление уравнений химических реакций» был понятным и познавательным. Если у вас возникли вопросы, пишите их в комментарии. Если вопросов нет, то переходите к следующему уроку.
Источник статьи: http://himi4ka.ru/arhiv-urokov/urok-12-sostavlenie-uravnenij-himicheskih-reakcij.html
Уравнение и его корни: определения, примеры
Содержание:
После того, как мы изучили понятие равенств, а именно один из их видов – числовые равенства, можно перейти к еще одному важному виду – уравнениям. В рамках данного материала мы объясним, что такое уравнение и его корень, сформулируем основные определения и приведем различные примеры уравнений и нахождения их корней.
Понятие уравнения
Обычно понятие уравнения изучается в самом начале школьного курса алгебры. Тогда оно определяется так:
Уравнением называется равенство с неизвестным числом, которое нужно найти.
Принято обозначать неизвестные маленькими латинскими буквами, например, t , r , m др., но чаще всего используются x , y , z . Иными словами, уравнение определяет форма его записи, то есть равенство будет уравнением только тогда, когда будет приведен к определенному виду – в нем должна быть буква, значение которое надо найти.
Приведем несколько примеров простейших уравнений. Это могут быть равенства вида x = 5 , y = 6 и т.д., а также те, что включают в себя арифметические действия, к примеру, x + 7 = 38 , z − 4 = 2 , 8 · t = 4 , 6 : x = 3 .
После того, как изучено понятие скобок, появляется понятие уравнений со скобками. К ним относятся 7 · ( x − 1 ) = 19 , x + 6 · ( x + 6 · ( x − 8 ) ) = 3 и др. Буква, которую надо найти, может встречаться не один раз, а несколько, как, например, в уравнении x + 2 + 4 · x − 2 − x = 10 . Также неизвестные могут быть расположены не только слева, но и справа или в обеих частях одновременно, например, x · ( 8 + 1 ) − 7 = 8 , 3 − 3 = z + 3 или 8 · x − 9 = 2 · ( x + 17 ) .
Далее, после того, как ученики знакомятся с понятием целых, действительных, рациональных, натуральных чисел, а также логарифмами, корнями и степенями, появляются новые уравнения, включающие в себя все эти объекты. Примерам таких выражений мы посвятили отдельную статью.
В программе за 7 класс впервые возникает понятие переменных. Это такие буквы, которые могут принимать разные значения (подробнее см. в статье о числовых, буквенных выражениях и выражениях с переменными). Основываясь на этом понятии, мы можем дать новое определение уравнению:
Уравнение – это равенство, включающее в себя переменную, значение которой нужно вычислить.
То есть, к примеру, выражение x + 3 = 6 · x + 7 – это уравнение с переменной x , а 3 · y − 1 + y = 0 – уравнение с переменной y .
В одном уравнении может быть не одна переменная, а две и более. Их называют соответственно уравнениями с двумя, тремя переменными и др. Запишем определение:
Уравнениями с двумя (тремя, четырьмя и более) переменными называют уравнения, которые включают в себя соответствующее количество неизвестных.
К примеру, равенство вида 3 , 7 · x + 0 , 6 = 1 является уравнением с одной переменной x , а x − z = 5 – уравнением с двумя переменными x и z . Примером уравнения с тремя переменными может быть выражение x 2 + ( y − 6 ) 2 + ( z + 0 , 6 ) 2 = 26 .
Корень уравнения
Когда мы говорим об уравнении, сразу возникает необходимость определиться с понятием его корня. Попробуем объяснить, что оно означает.
Нам дано некое уравнение, включающее в себя одну переменную. Если мы подставим вместо неизвестной буквы число, то уравнение станет числовым равенством – верным или неверным. Так, если в уравнении a + 1 = 5 мы заменим букву числом 2 , то равенство станет неверным, а если 4 , то получится верное равенство 4 + 1 = 5 .
Нас больше интересуют именно те значения, с которыми переменная обратится в верное равенство. Они и называются корнями или решениями. Запишем определение.
Корнем уравнения называют такое значение переменной, которое обращает данное уравнение в верное равенство.
Корень также можно назвать решением, или наоборот – оба эти понятия означают одно и то же.
Возьмем пример для пояснения этого определения. Выше мы приводили уравнение a + 1 = 5 . Согласно определению, корнем в данном случае будет 4 , потому что при подстановке вместо буквы оно дает верное числовое равенство, а двойка не будет решением, поскольку ей отвечает неверное равенство 2 + 1 = 5 .
Сколько корней может иметь одно уравнение? Любое ли уравнение имеет корень? Ответим на эти вопросы.
Уравнения, не имеющие ни одного корня, тоже существуют. Примером может быть 0 · x = 5 . Мы можем подставить в него бесконечно много разных чисел, но ни одно из них не превратит его в верное равенство, поскольку умножение на 0 всегда дает 0 .
Также бывают уравнения, имеющие несколько корней. У них может быть как конечное, так и бесконечно большое количество корней.
Так, в уравнении x − 2 = 4 есть только один корень – шесть, в x 2 = 9 два корня – три и минус три, в x · ( x − 1 ) · ( x − 2 ) = 0 три корня – нуль, один и два, в уравнении x=x корней бесконечно много.
Теперь поясним, как правильно записывать корни уравнения. Если их нет, то мы так и пишем: «уравнение корней не имеет». Можно также в этом случае указать знак пустого множества ∅ . Если корни есть, то пишем их через запятую или указываем как элементы множества, заключив в фигурные скобки. Так, если у какого-либо уравнения есть три корня — 2 , 1 и 5 , то пишем — 2 , 1 , 5 или < - 2 , 1 , 5 >.
Допускается запись корней в виде простейших равенств. Так, если неизвестная в уравнении обозначена буквой y , а корнями являются 2 и 7 , то мы пишем y = 2 и y = 7 . Иногда к буквам добавляются нижние индексы, например, x 1 = 3 , x 2 = 5 . Таким образом мы указываем на номера корней. Если решений у уравнения бесконечно много, то мы записываем ответ как числовой промежуток или используем общепринятые обозначения: множество натуральных чисел обозначается N , целых – Z , действительных – R . Скажем, если нам надо записать, что решением уравнения будет любое целое число, то мы пишем, что x ∈ Z , а если любое действительное от единицы до девяти, то y ∈ 1 , 9 .
Когда у уравнения два, три корня или больше, то, как правило, говорят не о корнях, а о решениях уравнения. Сформулируем определение решения уравнения с несколькими переменными.
Решение уравнения с двумя, тремя и более переменными – это два, три и более значения переменных, которые обращают данное уравнение в верное числовое равенство.
Поясним определение на примерах.
Допустим, у нас есть выражение x + y = 7 , которое представляет из себя уравнение с двумя переменными. Подставим вместо первой единицу, а вместо второй двойку. У нас получится неверное равенство, значит, эта пара значений не будет решением данного уравнения. Если же мы возьмем пару 3 и 4 , то равенство станет верным, значит, мы нашли решение.
Такие уравнения тоже могут не иметь корней или иметь бесконечное их количество. Если нам надо записать два, три, четыре и более значений, то мы пишем их через запятую в круглых скобках. То есть в примере выше ответ будет выглядеть как ( 3 , 4 ) .
На практике чаще всего приходится иметь дело с уравнениями, содержащими одну переменную. Алгоритм их решения мы подробно рассмотрим в статье, посвященной решению уравнений.
Источник статьи: http://zaochnik.com/spravochnik/matematika/systems/uravnenie-i-ego-korni/