Углы в геометрии
Угол — это геометрическая фигура, которая состоит из двух лучей и вершины.
Вершина угла — это точка, в которой два луча берут начало.
Стороны угла — это лучи, которые образуют угол.
Например: 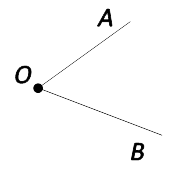
Стороны угла — « OA » и « OB ».
Для обозначения угла в тексте используется символ: 
Способы обозначения углов
Одной заглавной латинской буквой, указывающей его вершину.
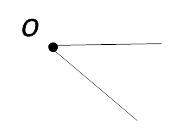

Тремя заглавными латинскими буквами, которыми обозначены вершина и две точки, расположенные на сторонах угла.
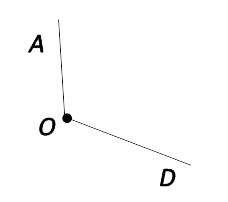

Называть угол можно с любого края, но НЕ с вершины.
Угол с рисунка выше имеет два названия: 

При таком обозначении вершина угла должна всегда находиться в середине названия.
- Двумя строчными латинскими буквами.
Угол:
fn
Единица измерения углов — градусы. Углы измеряют с помощью специального прибора — транспортира.
Для обозначения градусов в тексте используется символ: °
50 градусов обозначаются так: « 50° »
Виды углов
| Вид угла | Размер в градусах | Пример |
|---|---|---|
| Прямой | Равен 90° | 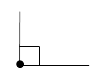 |
| Острый | Меньше 90° | 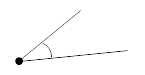 |
| Тупой | Больше 90° | 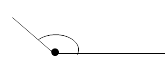 |
| Развернутый | Равен 180° | 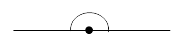 |
Два угла могут иметь одну общую сторону.
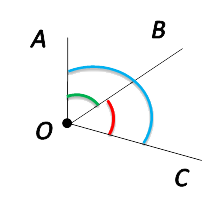
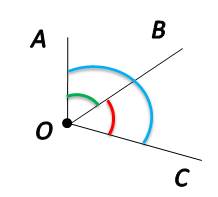
Обратите внимание на рисунок ниже. Попробуйте сосчитать и назвать все углы на изображении.
Если насчитали три угла, то вы правы. Давайте их назовём:
AOB
BOC
AOC
Углы 

Источник статьи: http://math-prosto.ru/?page=pages/geometry_primary/angle.php
Угол. Обозначение углов
Угол — геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки.
На рис. 1 лучи АВ и АС — стороны угла, точка А — вершина угла.
При записи угла в середине пишут букву, обозначающую его вершину. Сам угол на рис. 1 обозначают так: 






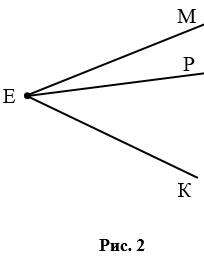
Если углы имеют общую вершину, то их нельзя обозначить одной буквой. Так на рис. 2 углы имеют общую вершину Е, поэтому мы можем использовать для данных углов только следующие обозначения: 











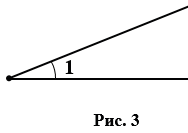
Также иногда углы обозначают цифрами, например, на рис.3 мы имеем 
Углы, как и отрезки, можно сравнивать между собой. Чтобы сравнить два угла можно наложить один угол на другой. Если при наложении одного угла на другой они совпадут, то эти углы равны.
Биссектриса — луч, который делит угол на два равных угла. На рис. 4 углы НОМ и DОМ равны, значит, луч ОМ — биссектриса угла НОD.
Прямой угол — угол, который можно построить с помощью угольника (рис. 5).
Если начертить два прямых угла с общей вершиной и одной общей стороной, то две другие стороны этих углов составят прямую (рис. 6). Считают, что лучи, составляющие прямую, также образуют угол, который называют развернутым.
На рис. 6 


Развернутый угол равен двум прямым углам, а прямой угол составляет половину развернутого.
Острый угол — угол, который меньше прямого угла. На рис. 7 
Тупой угол — угол, который больше прямого угла, но меньше развернутого. На рис. 8 
Поделись с друзьями в социальных сетях:
Источник статьи: http://budu5.com/manual/chapter/2262
Угол. Основные понятия.
Когда два луча (AO и OB) исходят из одной точки, то фигура, сформированная этими лучами (вместе с частью плоскости, ограниченной ими), называется углом.
Лучи, образующие угол называются сторонами. Точка из которой они исходят — вершиной угла.
Стороны угла следует представлять себе бесконечно продолженными от вершины.
Угол обыкновенно обозначается тремя буквами, из которых средняя ставится у вершины, а крайние у каких-нибудь точек сторон. Например, говорят “угол АОВ или угол ВОА”. Но можно обозначать угол и одной буквой, поставленной у вершины, если при этой вершине других углов нет. Мы иногда будем обозначать угол цифрой, поставленной внутри угла у вершины. Слово “угол” на письме часто заменяется знаком /.
Когда два луча исходят из одной точки, то строго говорят, что они образуют не один угол, а два угла.
Эти два угла равны друг другу лишь в том случае, когда лучи AO и OB составляют одну прямую.
Такой угол называют развернутым углом.
Два угла считаются равными углами, если при наложении они могут совместиться.
Мы принимаем как очевидное, что внутри всякого угла из его вершины можно провести луч (и притом только один), который делит этот угол пополам. Такой луч называется биссектрисой угла.
Два угла (AOB и BOС) называются смежными, если одна сторона у них общая, а две другие стороны составляют прямую линию.
Когда два смежных угла равны (черт. 2), то общая сторона их OB называется перпендикуляром к прямой AC, на которой лежат другие стороны.
Если же смежные углы неравны (черт. 1), то общая сторона OB называется наклонной к AC.
В том и в другом случае точка O называется основанием (перпендикуляра или наклонной).
Из всякой точки прямой можно, по ту и другую сторону от этой прямой, восставить к ней перпендикуляр и притом только один.
Каждый из равных смежных углов называется прямым. Прямой угол представляет собой постоянную величину равную 90 0 (ее обыкновенно обозначают знаком d, т.е. начальной буквой французского слова «droit» — прямой). Вследствие этого обыкновенные углы сравнивают по величине с прямым углом.
Всякий развернутый углом равен 2 d = 180°.
Всякий угол (АОС), меньший прямого угла (АОВ) называется острым.
Всякий угол (AOD) больший прямого называется тупым.
Источник статьи: http://www.calc.ru/Ugol-Osnovnyye-Ponyatiya.html
Способы обозначения углов
- Тремя заглавными латинскими буквами, которыми обозначены вершина и две точки, расположенные на сторонах угла.


Называть угол можно с любого края, но НЕ с вершины.
Угол с рисунка выше имеет два названия: 



При таком обозначении вершина угла должна всегда находиться в середине названия.
| Вид угла | Размер в градусах | Пример |
| Прямой | Равен 90° |  |
| Острый | Меньше 90° |  |
| Тупой | Больше 90° |  |
| Развернутый | Равен 180° |  |


Два угла могут иметь одну общую сторону.
Обратите внимание на рисунок ниже. Попробуйте сосчитать и назвать все углы на изображении.
Если насчитали три угла, то вы правы. Давайте их назавём:
AOB
BOC
AOC
Углы 

Познакомимся с основными фигурами геометрии.


Прямоугольник — это фигура, которая имеет четыре стороны и четыре прямых угла.
У прямоугольника противоположные стороны равны.
В геометрии прямоугольник обозначают четырьмя заглавными латинскими буквами.
Противоположные стороны прямоугольника ABCD: AB = CD, BC = DA.
Углы: 





Квадрат — это прямоугольник, у которого все стороны равны.
В геометрии квадрат, также как и прямоугольник, обозначают четырьмя большими латинскими буквами.
Стороны квадрата KLFM: KL = LF = FM = MK.
Углы: 





Треугольник — это геометрическая фигура, которая имеет три стороны и три угла (вершины треугольника).
Треугольник обозначается тремя заглавными латинскими буквами, перед которыми ставится знак: 
Треугольник EFG — 
| Вид треугольника | Углы треугольника | Пример |
| Прямоугольный | Один угол прямой, два других острых. |  |
| Остроугольный | Все углы острые |  |
| Тупоугольный | Один угол тупой, два других — острые |  |


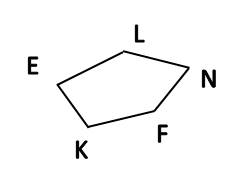
Многоугольники — это геометрические фигуры различной формы.
Вершины многоугольника — это точки, соединяющие отрезки, из которых состоит многоугольник.
Стороны многоугольника — это отрезки, из которых состоит многоугольник.
- Вершины многоугольника — E, L, F, N, K.
- Стороны многоугольника — EL, LN, NF, FK, KE.


Окружность — это геометрическая фигура, образованная замкнутой кривой линией, все точки которой находятся на одинаковом расстоянии от центра.
Круг — это геометрическая фигура, которая ограничена окружностью.
Окружность — это граница круга.
Радиус круга — это расстояние от центра окружности до любой её точки.
Диаметр круга — это отрезок, который соединяет две точки окружности и проходит через её центр.
Диаметр круга равен двум его радиусам.
- Точка O — центр круга.
- AB — диаметр круга.
- OK — радиус круга.
- АB = 2 OK.
Источник статьи: http://mydocx.ru/8-21041.html

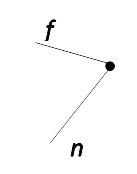 Угол:
Угол: