Как определить формулу, которая задаёт график изображённой линейной функции вида y=kx+b?
(Задание подобного вида есть в ВПР по математике за 7 класс)
нужно взять на графике две любые точки (на практике удобно брать те, которые с удобными целыми координатами). Например, пусть по графику видно, что при x = x1, y = y1, при x = x2, y = y2. Две точки (x1,y1) и (x2,y2) подставляются в формулу линейной функции и получается система уравнений относительно k и b. y1 = k*x1 + b, y2 = k*x2 + b. сначалы вычитаем одно из другого и найдем k. k = (y2 — y1)/(x2 — x1). После этого несложно найти b = (y1*x2-y2*x1)/(x2-x1)
Какой математический факт вас поражает больше всего?
Математика — обширна, в ней паралельно существуют совершенно разные науки. Уже в школе математика, начинаясь с основ арифметики и операций с натуральными числами, позже делится на алгебру и геометрию. В университете появляется математический анализ, аналитическая геометрия, комплексный анализ. А есть еще функциональный анализ, динамические системы, топология, теория кос, алгебры Ли, итд.
Но оказывается, что все разделы математики тесно связаны между собой. Например, есть такой математический факт:
В этой формуле соединены 5 фундаментальных математических констант из разных наук:
- 0 — «единичный элемент» в группе действительных чисел по сложению (арифметика)
- 1 — «единичный элемент» в поле действительных чисел по умножению (теория чисел)
- e — основание натуральных логарифмов, производная функции e^x равна самой себе (матанализ)
- pi — отношение длины окружности к ее диаметру (геометрия)
- i — «мнимая единица», основа комплексных чисел (комлексный анализ)
Зачем учёные рассчитывают число ПИ до такого сумасшедшего количества знаков? Из научного азарта, или это имеет математический смысл?
Мне тоже кажется, что весь этот разговор — про скорость конкретного процессора. Да, можно насчитать сколько угодно цифр этого числа. Практического приложения у результата, разумеется, нет.
Что человечеству дало доказательство гипотезы Пуанкаре?
Начнем с этого, что представляет собой гипотеза Пуанкаре. Ее определение звучит так: «Всякое замкнутое n-мерное многообразие гомотопически эквивалентно n-мерной сфере тогда и только тогда, когда оно гомеоморфно ей». Что это значит?
Представим себе шар из теста. При желании из него можно вылепить практически что угодно — фигурку животного, куб, трапецию или конус. Форм действительно очень много. В теперь возьмем бублик. Эта форма в математике называется «тор». Как бы вы ни старались, создать из тора шар или другой сплошной объект у вас не получится — отверстие никуда не денется. Собственно, сама гипотеза Пуанкаре состоит в том, что из фигуры можно сделать сферу, только если она не имеет форму тора.
Доказательство этой гипотезы российским математиком Григорием Перельманом привело к некоторым очень интересным выводам с точки зрения нашего понимания мира. Например, если эта гипотеза верна, соответсвенно, нашу Вселенную, представленную в виде сферы, можно свернуть в точку. Это, в свою очередь, значит, что теории Большого сжатия и Большого взрыва могут быть верны — доказанная гипотеза косвенно подтверждает их. Но это только один из эффектов доказанной «задачи тысячелетия». По мере совершенствования науки и техники мы несомненно найдем ей все больше применений.
Источник статьи: http://yandex.ru/q/question/hw.math/kak_opredelit_formulu_kotoraia_zadaiot_y_7dcfed02/
Линейная функция. Примеры решения задач (ЕГЭ – 2021)
Вот дурацкий пример, чтобы понять что такое функция.
Чтобы купить 1 айфон, нужно «развести» родителей на 70 тыс. рублей. (Разводить родителей не хорошо! Не делайте так никогда! 🙂 )
Количество айфонов, которые ты сможешь купить зависит от того, на сколько денег ты «разведешь» родителей.
Зависимость одной величины от другой математики называют ФУНКЦИЕЙ одной величины от другой.
Количество айфонов — это функция количества денег (иногда говорят «от количества денег).
Вес — это функция от съеденных круассанов. Чем меньше съел, тем меньше весишь.
Расстояние — это функция времени. Чем дольше ты будешь идти, тем больше пройдешь.
Ну а теперь перейдем к одному из видов функций – линейной функции.
Линейная функция
Но сначала официальное определение «Функции» – теперь ты его поймешь. Держи в уме: айфон – деньги, вес – круассаны, расстояние – время.
Функция – это правило, по которому каждому элементу одного множества (аргументу) ставится в соответствие некоторый (единственный!) элемент другого множества (множества значений функции).
То есть, если у тебя есть функция \( y=f\left( x \right)\), это значит что каждому допустимому значению переменной \( x\) (которую называют «аргументом») соответствует одно значение переменной \( y\) (называемой «функцией»).
Все дело в понятии «область определения»: для некоторых функций не все аргументы «одинаково полезны» — не все можно подставить в зависимость.
Например, для функции \( y=\sqrt
Ну и вернемся, наконец, к теме данной статьи.
Линейной называется функция вида \( y=kx+b\), где \( k\) и \( b\) – любые числа (они называются коэффициентами).
Другими словами, линейная функция – это такая зависимость, что функция прямо пропорциональна аргументу.
Как думаешь, почему она называется линейной?
Все просто: потому что графиком этой функции является прямая линия. Но об этом чуть позже.
Как уже говорилось в теме «Функции», важнейшими понятиями, связанными с любой функцией, являются ее область определения \( D\left( y \right)\) и область значений \( E\left( y \right)\).
Область определения линейной функции
Какими могут быть значения аргумента линейной функции \( y=kx+b\)? Правильно, любыми. Это значит, что область определения – все действительные числа:
или \( D\left( y \right)=\left( -\infty ;+\infty \right)\).
Область значений линейной функции
Тут тоже все просто: поскольку функция прямо пропорциональна аргументу, то чем больше аргумент \( x\), тем больше значение функции \( y\).
Значит, \( y\) так же как и \( x\) может принимать все возможные значения, то есть \( E\left( y \right)=\mathbb
Верно, да не всегда. Есть такие линейные функции, которые не могут принимать любые значения. Как думаешь, в каком случае возникают ограничения?
Вспомним формулу: \( y=kx+b\). Какие нужно выбрать коэффициенты \( k\) и \( b\), чтобы значение функции y не зависело от аргумента \( x\)?
А вот какие: \( b\) – любое, но \( k=0\). И правда, каким бы ни был аргумент \( x\), при умножении на \( k=0\) получится \( 0\)!
Тогда функция станет равна \( y=0\cdot x+b=b\), то есть она принимает одно и то же значение при всех \( x\):
\( y = kx + b:<\rm< >>\left[ \begin
Теперь рассмотрим несколько задач на линейную функцию.
Три задачи на линейную функцию
Решение задачи №1
Пусть начальное значение аргумента равно некому числу \( <
Чему была равна функция до увеличения? Подставляем аргумент в формулу:
После увеличения: \( <
Функция увеличилась на \( 4\). Как это записать на «математическом языке» (в виде уравнения)?
Изменение – это разность конечного и начального значений. Значит, нужно из конечного значения функции \( y\) вычесть начальное:
Решение задачи №2
Аналогично предыдущей задаче:
Начальное значение аргумента равно \( <
Начальное значение функции: \( <
В этот раз функция не увеличилась, а уменьшилась. Это значит, что конечное значение будет меньше начального, а значит, изменение (разность конечного и начального) будет отрицательным:
Определение прямой пропорциональной зависимости
Если проанализировать решения этих двух задач, можно прийти к важному выводу.
При изменении аргумента линейной функции на \( \Delta x\) функция изменяется на \( k\cdot \Delta x\). То есть изменение функции всегда ровно в \( \mathbf
\) раз больше изменения аргумента.
По сути это является определением прямой пропорциональной зависимости.
Решение задачи №3
Подставим известные значения аргумента и функции в формулу \( y=kx+b\):
Получили два уравнения относительно \( k\) и \( b\). Теперь достаточно решить систему этих двух уравнений:
Вычтем из первого уравнения второе:
\( 1-\left( -1 \right)=3k+b-\left( 5k+b \right)\text< >\Leftrightarrow \text< >2=-2k\text< >\Rightarrow \text< >k=-1\)
Подставим найденное значение k в первое уравнение:
\( 1=3\cdot \left( -1 \right)+b\text< >\Rightarrow \text< >b=4\)
Ответ: \( -1;\text< >4.\)
График линейной функции
Как я уже упоминал ранее, график такой функции – прямая линия.
Как известно из геометрии, прямую можно провести через две точки (то есть, если известны две точки, принадлежащие прямой, этого достаточно, чтобы ее начертить).
Предположим, у нас есть функция линейная функция \( y=2x+1\). Чтобы построить ее график, нужно вычислить координаты любых двух точек.
То есть нужно взять любые два значения аргумента \( x\) и вычислить соответствующие два значения функции.
Затем для каждой пары \( \left( x;y \right)\) найдем точку в системе координат, и проведем прямую через эти две точки.
Проще всего найти функцию, если аргумент \( x=0:y\left( 0 \right)=2\cdot 0+1=1\).
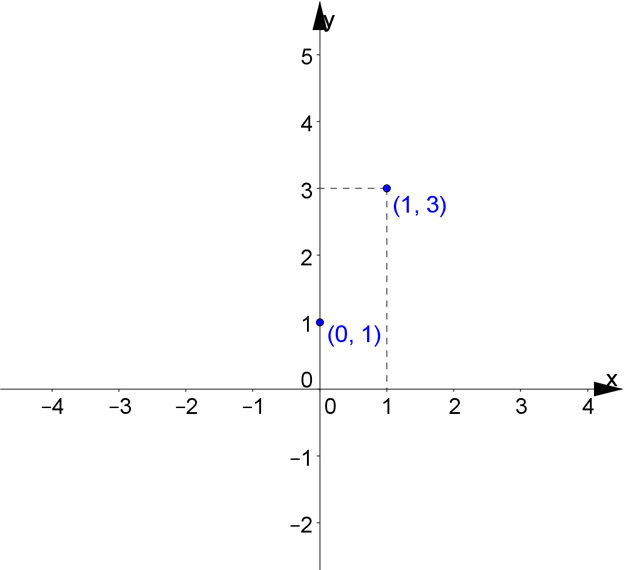
Итак, первая точка имеет координаты \( \left( 0;1 \right)\).
Теперь возьмем любое другое число в качестве \( x\), например, \( x=1:y\left( 1 \right)=2\cdot 1+1=3\).
Вторая точка имеет координаты \( \left( 1;3 \right)\).
Ставим эти две точки на координатной плоскости:
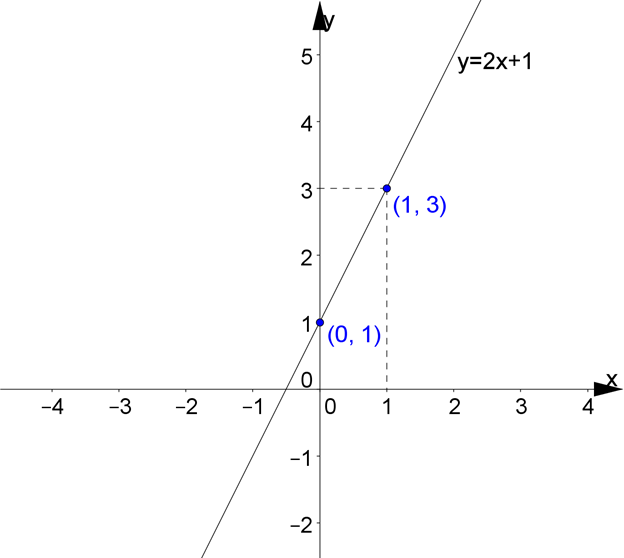
Теперь прикладываем линейку, и проводим прямую через эти две точки:
Вот и все, график построен!
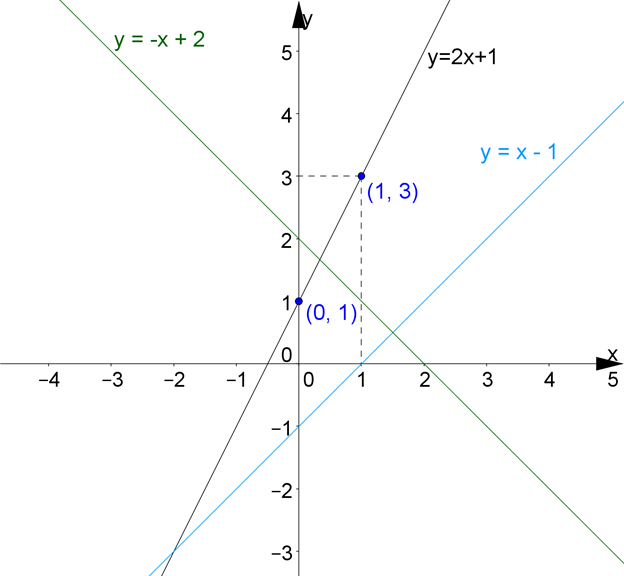
Давай теперь на этом же рисунке построим еще два графика: \( y=
Построй их самостоятельно так же: посчитай значение y для любых двух значений \( x\), отметь эти точки на рисунке и проведи через них прямую.
Видно, что все три прямые по-разному наклонены и в разных точках пересекают координатные оси. Все дело тут в коэффициентах \( \displaystyle k\) и \( \displaystyle b\).
Давай разберемся, на что они влияют.
Коэффициенты линейной функции
Для начала выясним, что делает коэффициент \( \displaystyle b\). Рассмотрим функцию \( \displaystyle y=x+b\), то есть \( \displaystyle k=1\).
Меняя \( \displaystyle b\) будем следить, что происходит с графиком.
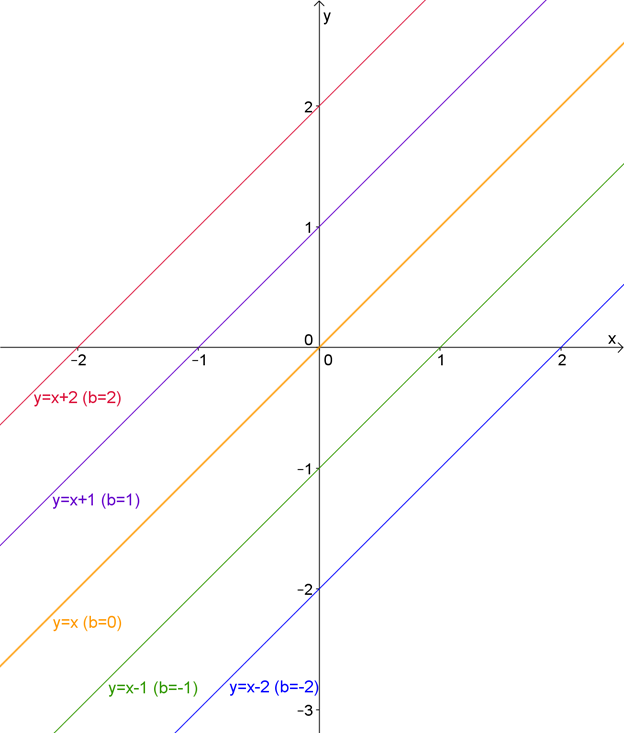
Итак, начертим графики для разных значений \( \displaystyle b:b=-2,\text< ->1,\text< >0,\text< >1,\text< >2\):
Что ты можешь сказать о них? Чем отличаются графики? Это сразу видно: чем больше \( \displaystyle b\), тем выше располагается прямая.
Более того, заметь такую вещь: график пересекает ось \( \displaystyle \mathbf
И правда. Как найти точку пересечения графика с осью \( \displaystyle y\)? Чему равен \( \displaystyle x\) в такой точке?
В любой точке оси ординат (это название оси \( \displaystyle y\), если ты забыл) \( \displaystyle x=0\).
Значит достаточно подставить \( \displaystyle x=0\) в функцию, и получим ординату пересечения графика с осью \( \displaystyle y\):
Теперь по поводу \( \displaystyle k\). Рассмотрим функцию \( \displaystyle \left( b=0 \right).\) Будем менять \( \displaystyle k\) и смотреть, что происходит с графиком.
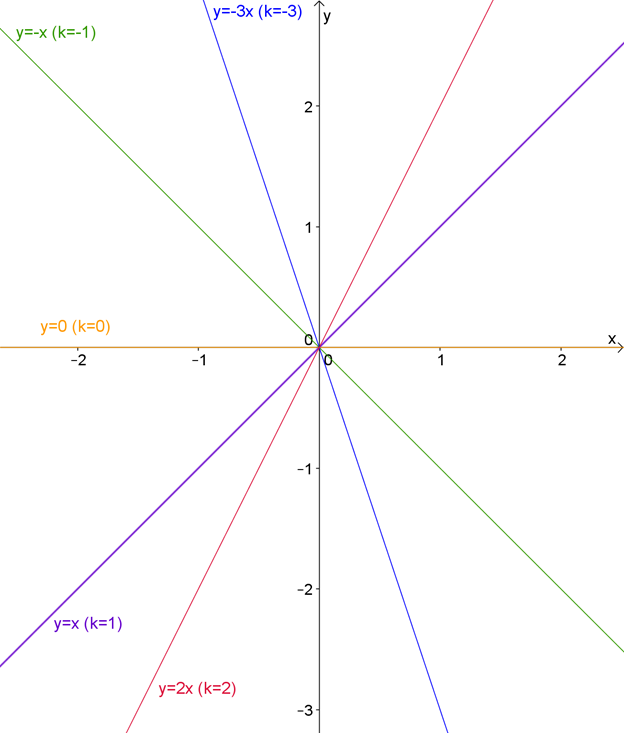
Построим графики для \( \displaystyle k=-3,\text< ->1,\text< >0,\text< >1,\text< >2:\)
Так, теперь ясно: \( \displaystyle k\) влияет на наклон графика.
Чем больше \( \displaystyle k\) по модулю (то есть несмотря на знак), тем «круче» (под большим углом к оси абсцисс – \( \displaystyle Ox\)) расположена прямая.
Если \( \displaystyle k>0\), график наклонен «вправо», при \( \displaystyle k
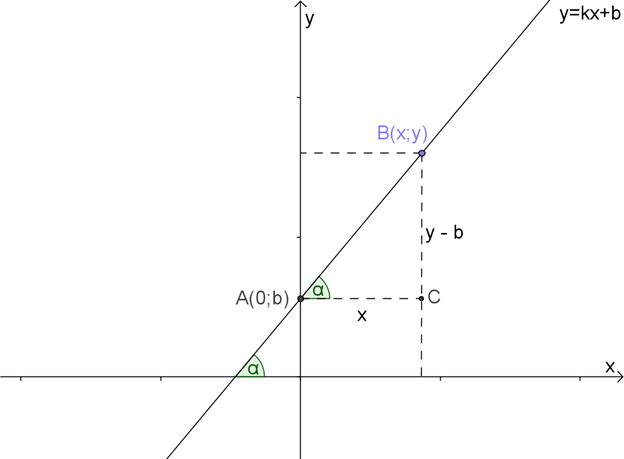
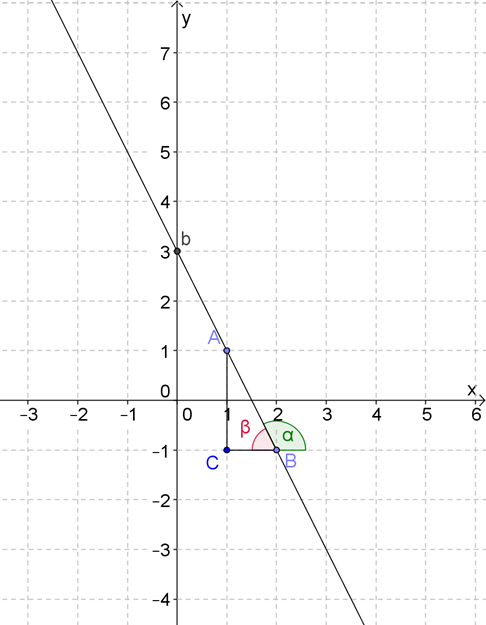
Выберем на графике две точки \( \displaystyle A\) и \( \displaystyle B\). Для простоты выберем точку \( \displaystyle A\) на пересечении графика с осью ординат. Точка \( \displaystyle B\) – в произвольном месте прямой, пусть ее координаты равны \( \displaystyle \left( x;y \right)\).
Рассмотрим прямоугольный треугольник \( \displaystyle ABC\), построенный на отрезке \( \displaystyle AB\) как на гипотенузе.
Из рисунка видно, что \( \displaystyle AC=x\), \( \displaystyle BC=y-b\).
Подставим \( \displaystyle y=kx+b\) в \( \displaystyle BC:BC=y-b=kx+b-b=kx\).
Получается, что \( BC = k \cdot AC<\rm< >> \Rightarrow <\rm< >>k = \frac<
Итак, коэффициент \( \displaystyle k\) равен тангенсу угла наклона графика, то есть угла между графиком и осью абсциссс.
Именно поэтому его (коэффициент \( \displaystyle k\)) обычно называют угловым коэффициентом.
В случае, когда \( k
Если же \( \displaystyle k=0\), тогда и \( <\mathop<\rm tg>\nolimits> \alpha = 0,\) следовательно \( \displaystyle \alpha =0\), то есть прямая параллельна оси абсцисс.
Понимать геометрическое значение коэффициентов очень важно, оно часто используется в различных задачах на линейную функцию.
Разбор еще 3-х задач на линейную функцию
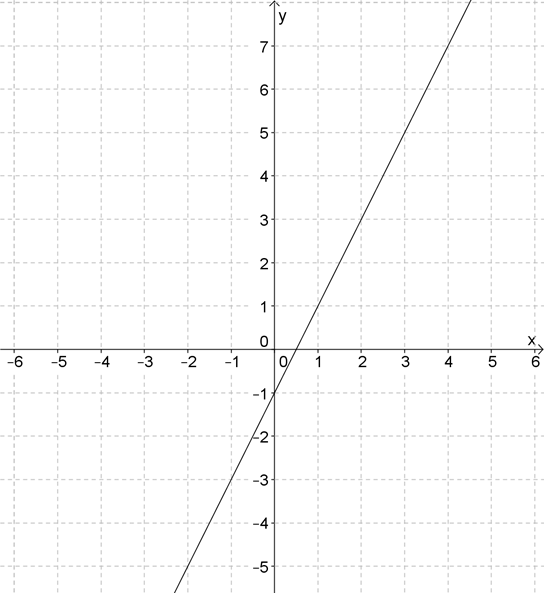
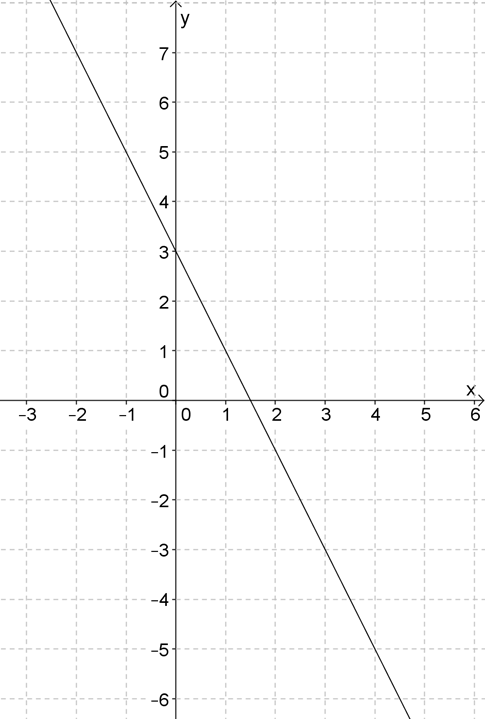
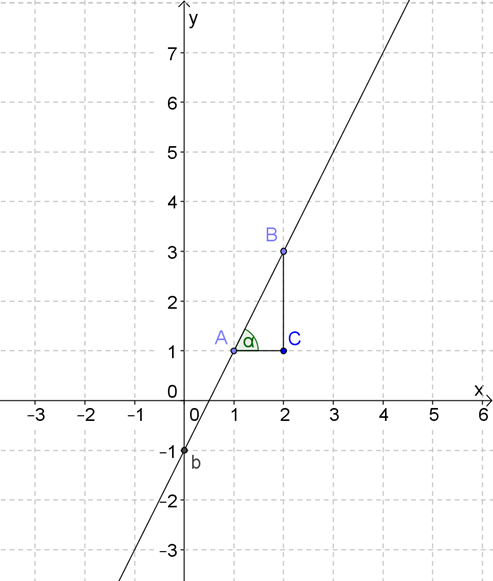
1. Найдите коэффициенты \( \displaystyle k\) и \( \displaystyle b\) линейной функции, график которой приведен на рисунке. Запишите уравнение этой функции.
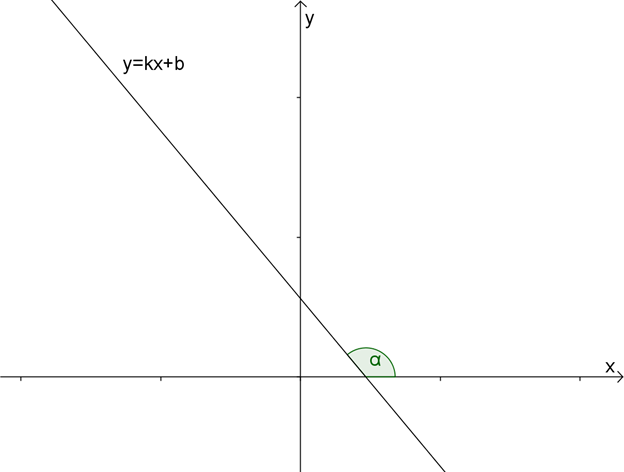
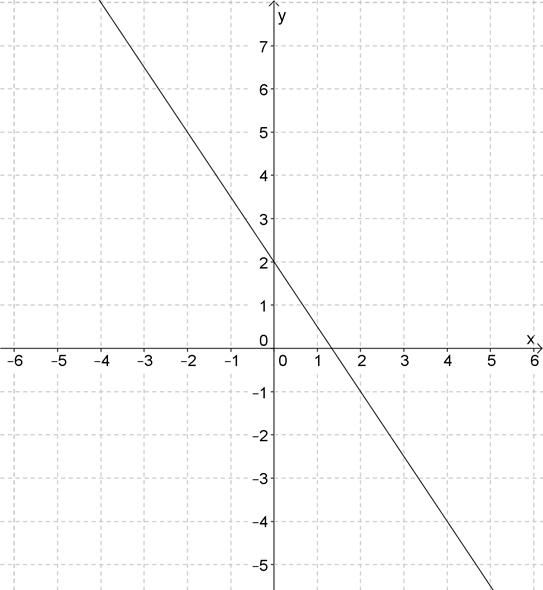
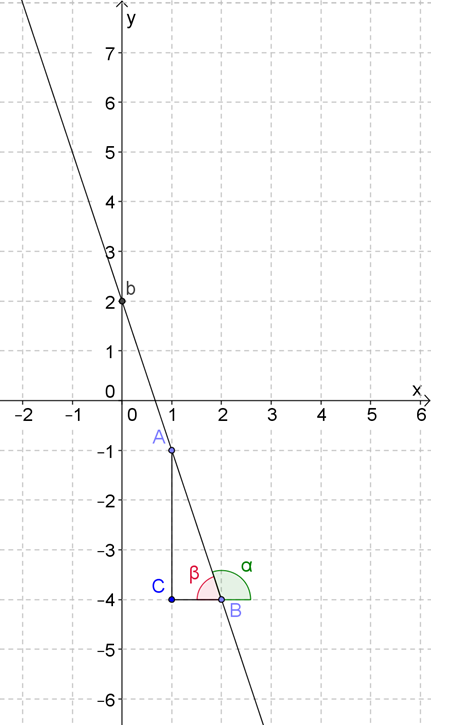
2. Найдите коэффициенты \( \displaystyle k\) и \( \displaystyle b\) линейной функции, график которой приведен на рисунке. Запишите уравнение этой функции.
3. График какой из функций изображен на рисунке?
Решение задачи №1
Коэффициент \( b\) найти проще простого – это ведь точка пересечения графика с осью \( \displaystyle Oy\):
Угловой коэффициент \( \displaystyle k\) – это тангенс угла наклона прямой.
Для его нахождения выберем две точки \( \displaystyle A\) и \( \displaystyle B\) на графике и построим прямоугольный треугольник с гипотенузой \( \displaystyle AB\):
Теперь можно составить уравнение этой прямой:
Решение задачи №2
Все аналогично предыдущей задаче.
Поскольку график наклонен «влево», угол между ним и осью абсцисс тупой, а значит, угловой коэффициент отрицательный.
Чтобы было проще найти тангенс угла наклона \( \alpha \), рассмотрим смежный с ним угол \( \beta \).
Тангенсы смежных углов равны по модулю, и противоположны по знаку:
Уравнение этой прямой выглядит так:
Решение задачи №3
И снова в первую очередь смотрим на \( \displaystyle b:b=3\). Значит, есть смысл рассматривать только функции a), b) и d).
Теперь посмотрим, каким должен быть угловой коэффициент?
Во-первых, он должен быть отрицательным, значит, выбрасываем ответ b). Остается a) и d).
Чтобы выбрать из них, придется найти тангенс угла наклона графика:
Отлично, значит уравнение этой прямой выглядит так:
То есть правильный ответ: a.
Точка пересечения графика с осью ординат – это коэффициент \( b\). А что можно сказать про точку пересечения с осью абсцисс?
В случае пересечения с осью \( Oy\) координата \( x=0\). При пересечении оси \( Ox\) – аналогично, координата \( y=0\):
Да это же простое линейное уравнение!
И действительно, такое линейное уравнение говорит нам, при каких значениях аргумента \( x\) функция \( y=0\), то есть корни такого уравнения – это координаты точек пересечения графика функции с осью абсцисс.
Это справедливо, кстати, для любой функции/уравнения.
Например, корни квадратного уравнения – это точки пересечения графика квадратичной функции – параболы – с осью \( Ox\).
Но подробнее об этом ты узнаешь в темах «Квадратные уравнения» и «Квадратичная функция».
КОРОТКО О ГЛАВНОМ
Линейная функция – это функция вида \( y=kx+b\), где \( k\) и \( b\) – любые числа (коэффициенты).
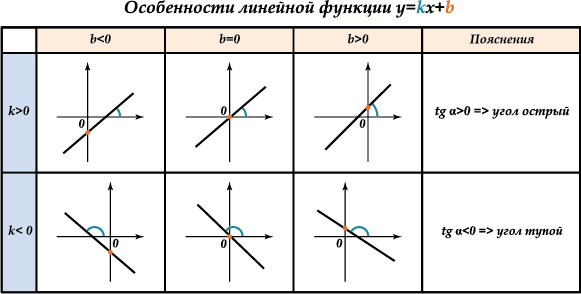
Рассмотрим, как коэффициенты влияют на месторасположение графика:
Общие варианты представлены на рисунке:
P.S. Последний бесценный совет 🙂
Ну вот, тема закончена. Если ты читаешь эти строки, значит, ты очень крут.
Потому что только 5% людей способны освоить что-то самостоятельно. И если ты дочитал до конца, ты попал в эти 5%!
Ты разобрался с теорией по этой теме. И, повторюсь, это… это просто супер! Ты уже лучше, чем абсолютное большинство твоих сверстников.
Проблема в том, что этого может не хватить…
Для успешной сдачи ОГЭ или ЕГЭ, для поступления в 10 класс или в институт на бюджет и, самое главное, для жизни.
Я не буду тебя ни в чем убеждать, просто скажу одну вещь…
Люди, получившие хорошее образование, зарабатывают намного больше, чем те, кто его не получил. Это статистика.
Главное то, что они более счастливы (есть такие исследования). Возможно, потому, что перед ними открывается гораздо больше возможностей и жизнь становится ярче? Не знаю…
Что нужно, чтобы быть наверняка лучше других на ОГЭ или ЕГЭ и быть в конечном итоге… более счастливым?
Набить руку, решая задачи.
На экзамене у тебя не будут спрашивать теорию.
Тебе нужно будет решать задачи на время. И, если ты не решал их (много!), ты обязательно где-нибудь глупо ошибешься или просто не успеешь. Это как в спорте: нужно много раз повторить, чтобы выиграть наверняка.
Найди где хочешь сборник, обязательно с решениями, подробным разбором и решай, решай, решай!
Можешь воспользоваться нашим сборником задач с подробным разбором, и мы их всячески рекомендуем, потому что они разбиты по темам, по типам и даже собраны в целую программу подготовки.
Если решишь набить руку с помощью наших задач, зайди на сайт 100gia и приобрети одну из программ.
А еще можешь зарегистрироваться и получить доступ к огромному количеству бесплатных материалов, видеоуроков, тестов.
Источник статьи: http://youclever.org/book/linejnaya-funktsiya-1/