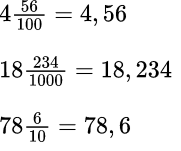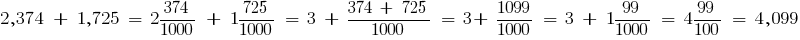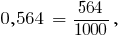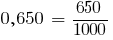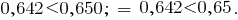СПАДИЛО.РУ
теория по математике 📈 числа и вычисления
Десятичная дробь — дробь, которая представляет собой способ представление числа в виде записи числа с запятой, где цифры перед запятой называются целой частью, а цифры после запятой – дробной частью (десятичной частью).
Десятичные дроби получают из записи обыкновенных дробей со знаменателем 10, 100, 1000 и так далее. Например, десятичные дроби:
4,56 – четыре целых пятьдесят шесть сотых 18,234 – восемнадцать целых двести тридцать четыре тысячных 78,6 – семьдесят восемь целых шесть десятых
Чтение десятичных дробей
Чтение десятичной части (десятых, сотых и так далее) зависит от количества цифр после запятой. Если цифра одна, то читают – десятых (в числе десять — один нуль, это соответствует одной цифре). Если две цифры после запятой, то читают – сотых (в сотне два нуля).
Десятичные дроби получаются из обыкновенных дробей:
Сложение (вычитание) десятичных дробей
Чтобы сложить (вычесть) в столбик две десятичные дроби нужно:
- Записать их друг под другом так, чтобы при записи запятая оказалась под запятой и соответствующий разряд под соответствующим.
- Уравнять количество знаков после запятой, добавляя недостающие нулями.
- Выполнить сложение (вычитание) в столбик, не обращая внимания на запятую.
- Поставить запятую под запятыми.
Если складывают (вычитают) целое число и десятичную дробь, то нужно поставить запятую после целого числа и приписать необходимое количество нулей после запятой.
Пример №1. Запись, где запятая под запятой и соответствующий разряд под соответствующим.
34,145 + 5,678 = 39,823
Пример №2. Запись, где также запятая под запятой, а во втором числе дописан нуль, чтобы уравнять количество знаков после запятой.
Пример №3. В первом слагаемом нет десятичной части, поэтому, после числа 56 поставили запятую и добавили нужное количество нулей.
Умножение десятичных дробей
При умножении двух десятичных дробей в столбик необходимо:
- Написать числа одно под другим, не обращая внимания на запятую
- Выполнить умножение в столбик
- В ответе отделить столько цифр справа запятой, сколько их в обоих множителях вместе. Если в одном из чисел нет запятой, то считать цифры только в одном числе.
Пример №4. Запись выполнена так, что цифры по правому краю записаны ровно одна под одной, то есть как при обычном умножении чисел в столбик. Умножение выполнено без учета запятой. В ответе справа отделены 4 цифры запятой, так как в первом множителе их 3 после запятой, а во втором – одна, в двух множителях вместе – четыре.
0,125 × 2,3 00375 0250 0,2875
Пример №5. Здесь показано умножение десятичной дроби и целого числа. Умножение выполнено без учета запятой. В ответе отделена справа запятой только одна цифра, так как только в первом множителе есть десятичная часть с одной цифрой после запятой.
Умножение десятичных дробей на 10, 100, 1000…
Чтобы умножить десятичную дробь на 10, 100, 1000 и так далее, нужно перенести запятую вправо на столько цифр, сколько нулей у множителя. Умножение в данном случае выполняется в строчку.
Пример №6. 2,456 × 10 = 24,56 Запятую в десятичной дроби перенесли вправо на 1 цифру, так как у 10 один нуль.
Пример №7. 0,45678 × 100 = 45,678 Запятую перенесли вправо на 2 цифры, так как у 100 два нуля. Нуль, стоящий в начале десятичной дроби, убрали, так как впереди целой части, отличной от нуля он не пишется.
Пример №8. 9,46 × 1000 = 9460 в данном случае при переносе запятой на три цифра не хватило одной, поэтому в конце числа приписали нуль, и в ответе получилось целое число.
Умножение десятичной дроби на разрядную единицу 0,1; 0,01; 0,001…
При умножении десятичной дроби на разрядную единицу 0,1; 0,01; 0,001 (и так далее) нужно перенести запятую на столько цифр влево, сколько цифр в данной разрядной единице после запятой. Умножение обычно выполняется в строчку устно.
Пример №9. 983,7821 × 0,01= 9,837821 Переносим запятые влево на 2 цифры, так как в числе 0,01 две цифры после запятой.
Пример №10. 8,7654 × 0,1 = 0,87654 Перенесли на 1 цифру влево, так как в числе 0,1 одна цифра после запятой. В данном случае перед 8 появился нуль, так как при переносе запятой слева цифр не оказалось.
Пример №11. 7,98 × 0,0001 = 0,000798 При переносе влево на 4 цифры не хватило трех, поэтому впереди поставили нули, а также нуль образуется и в целой части.
Деление десятичных дробей
- При делении десятичной дроби на целое число выполняют сначала деление целой части, а затем десятичной.
- При делении десятичной дроби на другую десятичную дробь необходимо в делителе убрать запятую, а в делимом передвинуть ее вправо на столько цифр, сколько их в делителе после запятой. Затем выполнить деление на целое число.
- Есть случаи, когда цифр после запятой при переносе запятой у дроби не хватает. Тогда необходимо дополнить число нулями.
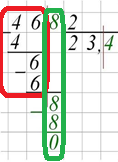
Пример №12. Деление десятичной дроби на целое число. 46,8 : 2 = 23,4
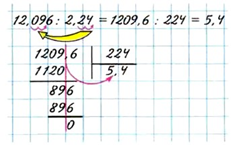
Пример №13. Деление десятичной дроби на десятичную дробь. 12,096 : 2,24 = 5,4 Из данного примера видно, что деление десятичных дробей обязательно сводится к делению на целое число.
Пример №14. 276,3 : 0,003 = 276300 : 3 = 92100. Здесь видно, что не хватает двух цифр в числе 276,3 и поэтому при переносе запятой к нему приписали два нуля. Затем выполнили деление двух целых чисел.
Деление десятичной дроби на 10, 100, 1000…
При делении десятичной дроби на 10,100, 1000 и так далее нужно перенести запятую на столько цифр влево, сколько нулей в данном числе. Деление выполняется в строчку устно.
Пример №16. 134,987 : 1000 = 0,134987 Перенесли запятую на три цифры влево, так как у 1000 три нуля. В целой части поставили нуль, так как цифр не хватило.
Пример №17. 7,234 : 100 = 0,07234 Перенесли запятую влево на две цифры. Так как цифр не хватало, то недостающие заменили нулями.
Деление десятичной дроби на разрядную единицу 0,1; 0,01; 0,001…
При делении десятичной дроби на разрядную единицу 0,1; 0,01; 0,001 и так далее нужно перенести запятую на столько цифр вправо, сколько цифр в данной разрядной единице после запятой. Деление обычно выполняется в строчку устно.
Пример №19. 41,234 : 0,01 = 4123,4 Перенос запятой на 2 цифры вправо, так как в числе 0,01 две цифры после запятой.
Пример №20. 56,91 : 0,001 = 56910 При переносе запятой на три цифры вправо приписали один нуль, так как одной цифры не хватило.
Источник статьи: http://spadilo.ru/desyatichnye-drobi/
Десятичные дроби
— дробь, знаменатель которого 10 n , где n — натуральное число.
Записан десятичная дробь читается согласно схемы
| 1 | 2 | 3 | 4 | , | 5 | 6 | 7 | 8 |
| тысячи | сотни | десятки | единицы | десятые | сотые | тысячные | десятитысячные |
Например десятичная дробь 10,436 читается «десять целых четыреста тридцать шесть тысячных».
Среди дробей наиболее часто употребляемыми в повседневной жизни есть дроби со знаменателями 10, 100, 1000 и т.д.
Например, 10 г 
1мм 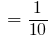
2см 5мм 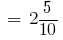
Числа со знаменателями 10, 100, 1000 и т. д. договорились записывать без знаменателя.
Сначала пишут целую часть, а потом числитель дробной части. Целую часть отделяют от дробной части запятой.
Например, вместо 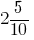
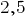
Любое число, знаменатель дробной части которого выражается единицей с одним или несколькими нулями, можно представить в виде десятичного дроби.
Если дробь правильная, то перед запятой пишут цифру 0.
Например, вместо 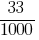
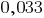
Обрати внимание! После запятой числитель дробной части должен иметь столько же цифр, сколько нулей в знаменателе.
Таблица разрядов десятичных дробей
Десятичная дробь, как и любое число, состоит из цифр (0,1,2,3,4,5,6,7,8,9).
Место каждой цифры в числе важное: оно определяет разряд числа.
Десятичная дробь состоит из целой части (все цифры до запятой) и дробной части (все цифры после запятой).
Целую часть десятичной дроби можно разбить на разряды также, как и натуральные числа: единицы, десятки, сотни, тысячи и т. д.
Дробная часть десятичной дроби разбивают на разряды так: десятые (в знаменателе обыкновенной дроби 10), сотые (десятые (в знаменателе обыкновенной дроби 100), тысячные (десятые (в знаменателе обыкновенной дроби 1000) и т.д.
Таблицу разрядов можно дополнить любым нужным количеством столбцов.
- 1-й разряд после запятой — разряд десятых,
- 2-й разряд после запятой — разряд сотых,
- 3-й разряд после запятой — разряд тысячных,
- 4-й разряд после запятой — разряд десятитысячных,
- 5-й разряд после запятой — разряд стотысячных,
- 6-й разряд после запятой — разряд миллионных,
- 7-й разряд после запятой — разряд десятимиллионным,
- 8-й разряд после запятой — разряд стомільйонних.
Сложение и вычитание десятичных дробей
Чтобы добавить или вычесть десятичные дроби, нужно:
- Уравнять в этих дробях количество знаков после запятой;
- Записать их друг под другом так, чтобы запятая была записана под запятой;
- Выполнить сложение (вычитание), не обращая внимания на запятую;
- Поставить в ответе запятую под запятой в данных дробях.
Свойства сложения для десятичных дробей:
a + b = b + a — переставная свойство
(a + b) + c = a + ( b + c ) — связующее свойство
Умножение десятичных дробей
Чтобы перемножить две десятичные дроби, надо:
1. выполнить умножение, не обращая внимания на запятые;
2. отделить запятой столько цифр справа, сколько их после запятой в обоих множителях вместе.
Подробнее читайте здесь
Деление десятичных дробей
Чтобы поделить десятичную дробь на натуральное число, надо:
1. разделить дробь на это число, не обращая внимания на запятую;
2. поставить в частном запятую, когда закончится делення целой части.
Подробнее читайте здесь
Сравнение десятичных дробей
Чтобы сравнить две десятичные дроби, надо сначала уравнять у них число десятичных знаков, приписав к одной из них справа нули, а потом, отбросив запятую, сравнить получившиеся натуральные числа.
Сравним две десятичные дроби 0,642 и 0,65. Уравняем число десятичных знаков, приписав к числу 0,65 дело ноль. Получим дроби 0,564 и 0,650.
Из двух дробей с одинаковыми знаменателями, больше то дробь, который имеет больший числитель.
Так как 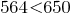
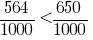
Десятичные дроби можно сравнивать и по разрядам.
В десятичных дробях 26,63 и 6,553 достаточно сравнить целые части. Так как 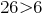
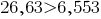
Конечные и бесконечные десятичные дроби
Определение: называется дробь, который содержит конечную количество цифр после запятой.
Определение: называется дробь, который не содержит конечной количества цифр после запятой.
Определение: (периодическим дробью) называется бесконечный дробь, в конце содержит группу цифр, которые повторяются.
называется группа цифр, которые повторяются. В предыдущем примере-это 89.
Периодическая десятичная дробь называется , если ее период начинается сразу после запятой, а период может содержать любое конечное число цифр.
Периодическая десятичная дробь называется если периодическая десятичная дробь содержит еще число, помещенное между целой частью и периодом. Число периодической дроби, стоящее между целой частью и периодом, называется передперіодом этой дроби.
Источник статьи: http://cubens.com/ru/handbook/fractional-numbers/decimal-fractions