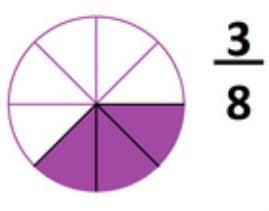
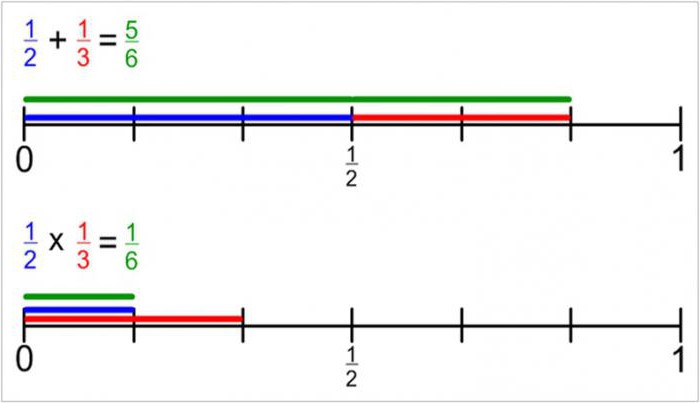
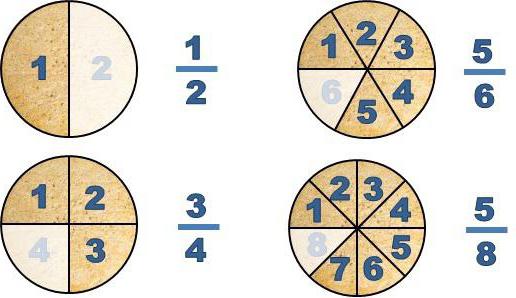
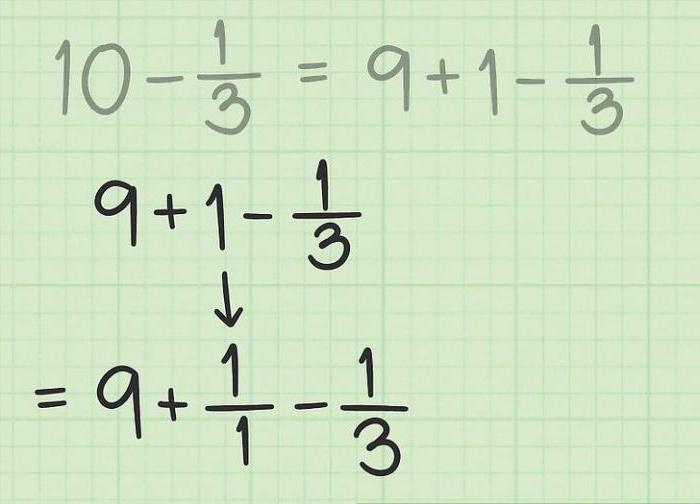Почему дроби называются правильными и неправильными?
фикл статей «Дроби»
ОБЫКНОВЕННЫЕ ДРОБИ
Ответ на этот вопрос вы найдёте в самом конце статьи, а начинаем, как обычно, с определений.
Обыкновенные дроби — это форма записи вида
где « — » — дробная черта ;
n — знаменатель ( натуральное число ; m — числитель ( целое число ), читается как «m-энных».
Так, ранее упомянутые, словесные формы записи некоторых дробей могут быть записаны в виде:
ДРОБНАЯ ЧЕРТА
О роли числителя и знаменателя говорилось в предыдущей публикации, здесь же мы отметим значение дробной черты .
Во-первых, само появление дробной черты сигнализирует, что перед нами обыкновенная дробь .
Во-вторых, поскольку обыкновенная дробь чаще всего образуется как результат деления натуральных чисел в случаях, когда делимое не кратно делителю (не делится на делитель нацело), то дробная черта часто равносильна знаку деления , например:
ЗНАМЕНАТЕЛЬ ДРОБИ НЕ МОЖЕТ БЫТЬ НУЛЁМ , поскольку ДЕЛИТЬ на 0 НЕЛЬЗЯ!
В случаях, когда числитель и знаменатель имеют разные знаки, значение дроби отрицательно:
Чтобы изменить знак дроби достаточно изменить знак либо у числителя, либо у знаменателя:
Далее будем рассматривать только положительные дроби, числитель и знаменатель которых положительны.
ПРАВИЛЬНЫЕ и НЕПРАВИЛЬНЫЕ ДРОБИ
В зависимости от результата сравнения числителя и знаменателя обыкновенной дроби различают правильные и неправильные дроби.
Правильная дробь — это обыкновенная дробь, числитель которой меньше знаменателя .
Правильная дробь действительно выражает «правильную» часть единицы, то есть часть, которая меньше целого:
Аликвотные дроби тоже относятся к правильным дробям:
К аликвотным дробям мы вернёмся позднее, после того, как рассмотрим сложение обыкновенных дробей.
Неправильная дробь — это обыкновенная дробь, числитель которой не меньше (больше или равен) знаменателю.
Название «неправильная» дано таким дробям не случайно. Всё дело в том, что ЧАСТЬ всегда воспринимается как нечто меньшее целого, в данном случае единицы, и не может быть больше или равной этому целой. Такая часть воспринимается как «неправильная», и эта «неправильность» перешла и на название соответствующих дробей.
Однако это различие между «правильными» и «неправильными» обыкновенными дробями не оказывает никакого влияния на арифметические действия с этими дробями, и сказывается только при их сравнении:
ПРАВИЛЬНАЯ ДРОБЬ МЕНЬШЕ НЕПРАВИЛЬНОЙ:
# хакнем_математика 👈 рубрика, содержащая интересный, познавательный контент по математике как для школьников, так и для взрослых 🥳
Автор: # себихов_александр 71 год, много лет проработал конструктором-технологом микроэлектронных приборов и узлов в одном из НИИ г. Саратова, затем преподавателем математики и физики.
Источник статьи: http://zen.yandex.ru/media/haknem_shkola/pochemu-drobi-nazyvaiutsia-pravilnymi-i-nepravilnymi-5f3c1442cae2755060ba3f71
Дроби обыкновенные правильные и неправильные, смешанные и составные.
Дробь в математике — число, состоящее из одной или нескольких частей (долей) единицы. Дроби являются частью поля рациональных чисел. По способу записи дроби делятся на 2 формата: обыкновенные вида 
Числитель дроби — число, показывающее количество взятых долей (находится в верхней части дроби – над чертой). Знаменатель дроби — число, показывающее, на сколько долей разделена единица (находится под чертой – в нижней части). Обыкновенные дроби, в свою очередь делятся на: правильные и неправильные, смешанные и составные. Обыкновенные дроби тесно связаны с единицами измерения. 1 метр содержит в себе 100 см. Что означает, что 1 м разделён на 100 равных долей. Таким образом, 1 см = 1/100 м (один сантиметр равен одной сотой метра).
или 3/5 (три пятых), здесь 3 — числитель, 5 — знаменатель. Если числитель меньше знаменателя, то дробь меньше единицы и называется правильной:
Если числитель равен знаменателю, дробь равна единице. Если числитель больше знаменателя, дробь больше единицы. В обоих последних случаях дробь называется неправильной:
Чтобы выделить наибольшее целое число, содержащееся в неправильной дроби, нужно разделить числитель на знаменатель. Если деление выполняется без остатка, то взятая неправильная дробь равна частному:
Если деление выполняется с остатком, то (неполное) частное дает искомое целое число, остаток же становится числителем дробной части; знаменатель дробной части остается прежним.
Число, содержащее целую и дробную части, называется смешанным. Дробная часть смешанного числа может быть и неправильной дробью. Тогда можно из дробной части выделить наибольшее целое число и представить смешанное число в таком виде, чтобы дробная часть стала правильной дробью (или вовсе исчезла).
К подобному виду обычно и приводят смешанные дроби.
Составные дроби.
Многоэтажной, или составной дробью является дробь, которая содержит в себе несколько горизонтальных (либо реже — наклонных) черт:



Источник статьи: http://www.calc.ru/Drobi-Obyknovennyye-Pravilnyye-I-Nepravilnyye-Smeshannyye-I-.html
Правильные и неправильные дроби.
Виды дробей.
Как вы уже заметили дроби бывают разные. Например, \(\frac<1><2>, \frac<3><5>, \frac<5><7>, \frac<7><7>, \frac<13><5>, …\)
Делятся дроби на два вида правильные дроби и неправильные дроби.
В правильной дроби числитель меньше знаменателя, например, \(\frac<1><2>, \frac<3><5>, \frac<5><7>, …\)
В неправильной дроби числитель больше или равен знаменателю, например, \(\frac<7><7>, \frac<9><4>, \frac<13><5>, …\)
Правильная дробь всегда меньше единицы. Рассмотрим пример:
Единицу мы можем представить как дробь \(1 = \frac<3><3>\)
Знаменатели одинаковые равны числу 3, далее сравниваем числители.
Вопросы по теме “Правильные или неправильные дроби”:
Может ли правильная дробь быть больше 1?
Ответ: нет.
Может ли правильная дробь равна 1?
Ответ: нет.
Может ли неправильная дробь меньше 1?
Ответ: нет.
Пример №1:
Напишите:
а) все правильные дроби со знаменателем 8;
б) все неправильные дроби с числителем 4.
Решение:
а) У правильных дробей знаменатель больше числителя. Нам нужно в числитель поставить числа меньшие 8.
\(\frac<1><8>, \frac<2><8>, \frac<3><8>, \frac<4><8>, \frac<5><8>, \frac<6><8>, \frac<7><8>.\)
б) В неправильной дроби числитель больше знаменателя. Нам нужно в знаменатель поставить числа меньшие 4.
\(\frac<4><4>, \frac<4><3>, \frac<4><2>, \frac<4><1>.\)
Пример №2:
При каких значениях b дробь:
а) \(\frac<12>\) будет правильной;
б) \(\frac<9>\) будет не правильной.
Решение:
а) b может принимать значения 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11.
б) b может принимать значения 1, 2, 3, 4, 5, 6, 7, 8, 9.
Задача №1:
Сколько минут в часе? Какую часть часа составляет 11 мин.?
Ответ: В часе 60 минут. Три минуты составят \(\frac<11><60>\) часа.
Источник статьи: http://tutomath.ru/5-klass/pravilnye-i-nepravilnye-drobi.html
Что такое правильная дробь? Правильная и неправильная дробь: правила
С дробями мы сталкиваемся в жизни гораздо раньше, чем начинается их изучение в школе. Если разрезать целое яблоко пополам, то мы получим часть фрукта – ½. Разрежем ещё раз – будет ¼. Это и есть дроби. И все, казалось бы, просто. Для взрослого человека. Для ребенка же (а данную тему начинают изучать в конце младшей школы) абстрактные математические понятия ещё пугающе непонятны, и преподаватель должен доступно объяснить, что такое правильная дробь и неправильная, обыкновенная и десятичная, какие операции можно с ними совершать и, главное, для чего всё это нужно.
Какие бывают дроби
Знакомство с новой темой в школе начинается с обыкновенных дробей. Их легко узнать по горизонтальной черте, разделяющей два числа – сверху и снизу. Верхнее называется числителем, нижнее – знаменателем. Существует и строчный вариант написания неправильных и правильных обыкновенных дробей – через косую черту, например: ½, 4/9, 384/183. Такой вариант используется, когда высота строки ограничена и нет возможности применить «двухэтажную» форму записи. Почему? Да потому что она удобнее. Чуть позже мы в этом убедимся.
Новые понятия
Вернемся к обыкновенным дробям. Они бывают двух видов.
Определение правильной дроби звучит следующим образом: это такая дробь, числитель которой меньше знаменателя. Почему это важно? Сейчас увидим!
У вас есть несколько яблок, разделенных на половинки. Всего – 5 частей. Как вы скажете: у вас «два с половиной» или «пять вторых» яблока? Конечно, первый вариант звучит естественнее, и при разговоре с друзьями мы воспользуемся им. А вот если потребуется посчитать, сколько фруктов достанется каждому, если в компании пять человек, мы запишем число 5/2 и разделим его на 5 – с точки зрения математики это будет нагляднее.
Основное свойство дроби
Если числитель и знаменатель дроби одновременно умножить или разделить на одно и то же число, её величина не изменится. Представьте: торт порезали на 4 равные части и дали вам одну. Такой же торт порезали на восемь частей и дали вам две. Не всё ли равно? Ведь ¼ и 2/8 – это одно и то же!
Сокращение
Авторы задач и примеров в учебниках по математике зачастую стремятся запутать учеников, предлагая громоздкие в написании дроби, которые на самом деле можно сократить. Вот пример правильной дроби: 167/334, который, казалось бы, выглядит очень «страшно». Но на самом деле мы можем записать его как ½. Число 334 делится на 167 без остатка – проделав такую операцию, мы получим 2.
Смешанные числа
Неправильную дробь можно представить в форме смешанного числа. Это когда целая часть вынесена вперед и записана на уровне горизонтальной черты. Фактически выражение принимает вид суммы: 11/2 = 5 + ½; 13/6 = 2 + 1/6 и так далее.
Можно осуществить и обратную операцию – для этого нужно целую часть умножить на знаменатель и прибавить полученное значение к числителю. Ничего сложного.
Умножение и деление
Как ни странно, умножать дроби проще, чем складывать. Всего-то и требуется — продлить горизонтальную черту: (2/3) * (3/5) = 2*3 / 3*5 = 2/5.
С делением тоже всё просто: нужно перемножить дроби крест-накрест: (7/8) / (14/15) = 7*15 / 8*14 = 15/16.
Сложение дробей
Что делать, если требуется осуществить сложение или вычитание дробей, а в знаменателе у них разные числа? Поступить так же, как с умножением, не получится – здесь следует понимать определение правильной дроби и её сущность. Нужно привести слагаемые к общему знаменателю, то есть в нижней части обеих дробей должны оказаться одинаковые числа.
Как же выбрать, к какому знаменателю приводить слагаемые? Это должно быть минимальное число, кратное обоим числам, стоящим в знаменателях дробей: для 1/3 и 1/9 это будет 9; для ½ и 1/7 – 14, потому что меньшего значения, делящегося без остатка на 2 и 7, не существует.
Использование
Для чего нужны неправильные дроби? Ведь гораздо удобнее сразу выделить целую часть, получить смешанное число – и дело с концом! Оказывается, если требуется выполнить умножение или деление двух дробей, выгоднее воспользоваться именно неправильными.
Возьмем следующий пример: (2 + 3/17) / (37 / 68).
Теперь всё встает на свои места! Запишем пример таким образом, чтобы всё стало очевидно: (37*68) / (17*37).
Сократим 37 в числителе и знаменателе и, наконец, разделим верхнюю и нижнюю части на 17. Вы же помните основное правило для правильной и неправильной дроби? Мы можем умножать и делить их на любое число, если делаем это одновременно для числителя и знаменателя.
Итак, получаем ответ: 4. Пример выглядел сложным, а ответ содержит всего одну цифру. В математике так часто происходит. Главное – не бояться и следовать простым правилам.
Распространенные ошибки
При осуществлении действий с дробями учащийся может легко совершить одну из популярных ошибок. Обычно они происходят из-за невнимательности, а иногда – из-за того, что изученный материал ещё не отложился в голове как следует.
Нередко сумма чисел, стоящая в числителе, вызывает желание сократить отдельные её компоненты. Допустим, в примере: (13 + 2) / 13, написанном без скобок (с горизонтальной чертой), многие ученики по неопытности зачеркивают 13 сверху и снизу. Но так делать нельзя ни в коем случае, ведь это грубая ошибка! Если бы вместо сложения стоял знак умножения, мы получили бы в ответе число 2. Но при осуществлении сложения никакие операции с одним из слагаемых не позволительны, только со всей суммой целиком.
Скобки
Помните, что в любых математических выражениях порядок действий определяется приоритетом знаков операций и наличием скобок. При прочих равных отсчёт очередности выполнения действий происходит слева направо. Это актуально и для дробей – выражение в числителе или знаменателе рассчитывается строго по этому правилу.
Ведь что такое правильная дробь? Это результат деления одного числа на другое. Если они не делятся нацело, получается дробь – вот и всё.
Как записать дробь на компьютере
Поскольку стандартные средства не всегда позволяют создать дробь, состоящую из двух «ярусов», ученики порой идут на различные ухищрения. Например, копируют числители и знаменатели в графический редактор «Пейнт» и склеивают их воедино, рисуя между ними горизонтальную линию. Конечно, есть более простой вариант, который, кстати, предоставляет и массу дополнительных возможностей, которые станут полезны вам в будущем.
Откройте «Майкрософт Ворд». Одна из панелей в верхней части экрана носит называние «Вставка» — нажмите её. Справа, в той стороне, где расположены значки закрытия и сворачивания окна, есть кнопка «Формула». Это именно то, что нам нужно!
Изучайте математику
Если вы учитесь в 5-6 классе, то уже скоро знание математики (в том числе – умение работать с дробями!) потребуется во многих школьных предметах. Практически в любой задаче по физике, при измерении массы веществ в химии, в геометрии и тригонометрии без дробей никак не обойтись. Уже скоро вы научитесь вычислять всё в уме, даже не записывая выражения на бумаге, но будут появляться всё более и более сложные примеры. Поэтому выучите, что такое правильная дробь и как с ней работать, не отставайте по учебной программе, своевременно делайте домашние задания, и тогда вы преуспеете.
Источник статьи: http://fb.ru/article/334649/chto-takoe-pravilnaya-drob-pravilnaya-i-nepravilnaya-drob-pravila