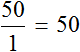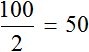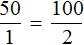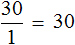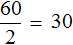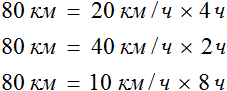Прямая и обратная пропорциональность
Пропорциональность — это взаимосвязь между двумя величинами, при которой изменение одной из них влечет за собой изменение другой во столько же раз.
Пропорциональность бывает прямой и обратной. В данном уроке мы рассмотрим каждую из них.
Прямая пропорциональность
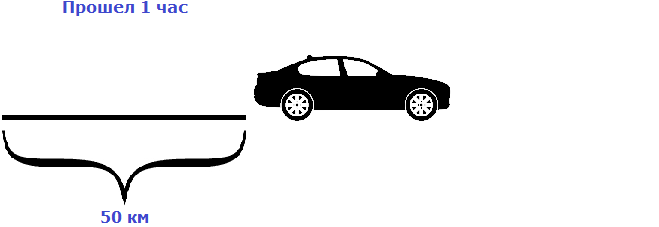
Предположим, что автомобиль двигается со скоростью 50 км/ч. Мы помним, что скорость это расстояние, пройденное за единицу времени (1 час, 1 минуту или 1 секунду). В нашем примере автомобиль двигается со скоростью 50 км/ч, то есть за один час он будет проезжать расстояние, равное пятидесяти километрам.
Изобразим на рисунке расстояние, пройденное автомобилем за 1 час
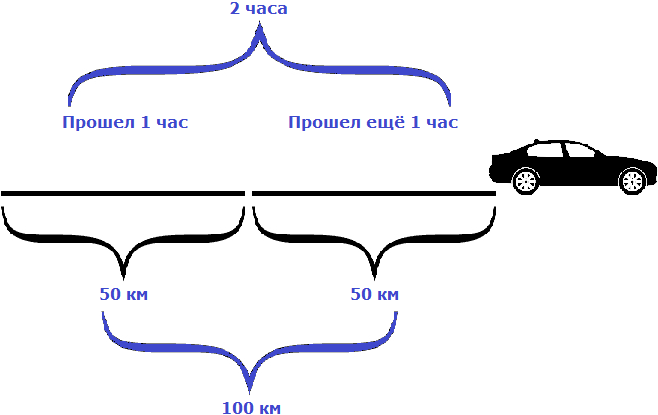
Пусть автомобиль проехал еще один час с той же скоростью, равной пятидесяти километрам в час. Тогда получится, что автомобиль проедет 100 км
Как видно из примера, увеличение времени в два раза привело к увеличению пройденного расстояния во столько же раз, то есть в два раза.
Такие величины, как время и расстояние называют прямо пропорциональными. А взаимосвязь между такими величинами называют прямой пропорциональностью.
Прямой пропорциональностью называют взаимосвязь между двумя величинами, при которой увеличение одной из них влечет за собой увеличение другой во столько же раз.
и наоборот, если одна величина уменьшается в определенное число раз, то другая уменьшается во столько же раз.
Предположим, что изначально планировалось проехать на автомобиле 100 км за 2 часа, но проехав 50 км, водитель решил отдохнуть. Тогда получится, что уменьшив расстояние в два раза, время уменьшится во столько же раз. Другими словами, уменьшение пройденного расстояния приведет к уменьшению времени во столько же раз.
Интересная особенность прямо пропорциональных величин заключается в том, что их отношение всегда постоянно. То есть при изменении значений прямо пропорциональных величин, их отношение остается неизменным.
В рассмотренном примере расстояние сначала было равно 50 км, а время одному часу. Отношение расстояния ко времени есть число 50.
Но мы увеличили время движения в 2 раза, сделав его равным двум часам. В результате пройденное расстояние увеличилось во столько же раза, то есть стало равно 100 км. Отношение ста километров к двум часам опять же есть число 50
Число 50 называют коэффициентом прямой пропорциональности. Он показывает сколько расстояния приходится на час движения. В данном случае коэффициент играет роль скорости движения, поскольку скорость это отношение пройденного расстояния ко времени.
Из прямо пропорциональных величин можно составлять пропорции. К примеру, отношения 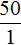
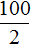
Это отношение можно прочитать следующим образом:
Пятьдесят километров так относятся к одному часу, как сто километров относятся к двум часам.
Пример 2. Стоимость и количество купленного товара являются прямо пропорциональными величинами. Если 1 кг конфет стоит 30 рублей, то 2 кг этих же конфет обойдутся в 60 рублей, 3 кг в 90 рублей. С увеличением стоимости купленного товара, его количество увеличивается во столько же раз.
Поскольку стоимость товара и его количество являются прямо пропорциональными величинами, то их отношение всегда постоянно.
Запишем чему равно отношение тридцати рублей к одному килограмму
Теперь запишем чему равно отношение шестидесяти рублей к двум килограммам. Это отношение опять же будет равно тридцати:
Здесь коэффициентом прямой пропорциональности является число 30. Этот коэффициент показывает сколько рублей приходится на килограмм конфет. В данном примере коэффициент играет роль цены одного килограмма товара, поскольку цена это отношение стоимости товара на его количество.
Обратная пропорциональность
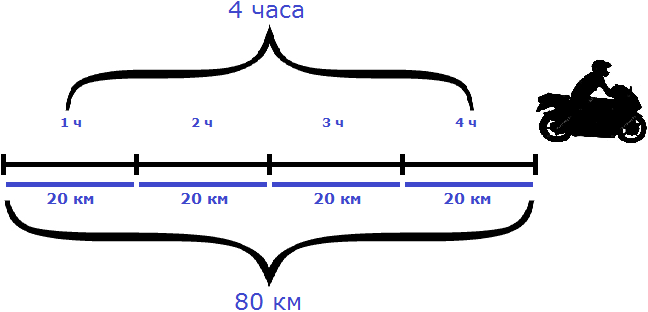
Рассмотрим следующий пример. Расстояние между двумя городами 80 км. Мотоциклист выехал из первого города, и со скоростью 20 км/ч доехал до второго города за 4 часа.
Если скорость мотоциклиста составила 20 км/ч это значит, что каждый час он проезжал расстояние равное двадцати километрам. Изобразим на рисунке расстояние, пройденное мотоциклистом, и время его движения:
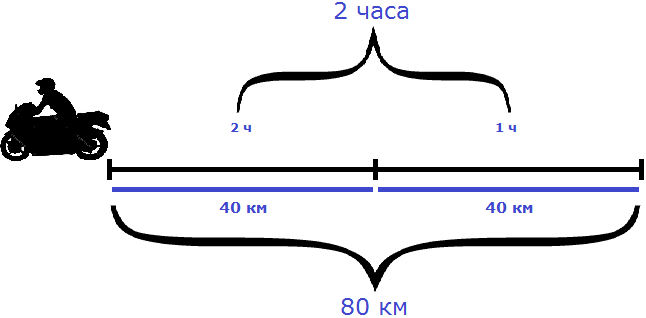
На обратном пути скорость мотоциклиста была 40 км/ч, и на тот же путь он затратил 2 часа.
Легко заметить, что при изменении скорости, время движения изменилось во столько же раз. Причем изменилось в обратную сторону — то есть скорость увеличилась, а время наоборот уменьшилось.
Такие величины, как скорость и время называют обратно пропорциональными. А взаимосвязь между такими величинами называют обратной пропорциональностью.
Обратной пропорциональностью называют взаимосвязь между двумя величинами, при которой увеличение одной из них влечет за собой уменьшение другой во столько же раз.
и наоборот, если одна величина уменьшается в определенное число раз, то другая увеличивается во столько же раз.
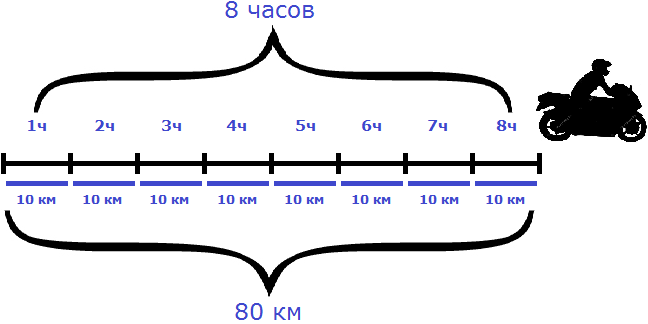
К примеру, если на обратном пути скорость мотоциклиста составила бы 10 км/ч, то те же 80 км он преодолел бы за 8 часов:
Как видно из примера, уменьшение скорости привело к увеличению времени движения во столько же раз.
Особенность обратно пропорциональных величин заключается в том, что их произведение всегда постоянно. То есть при изменении значений обратно пропорциональных величин, их произведение остается неизменным.
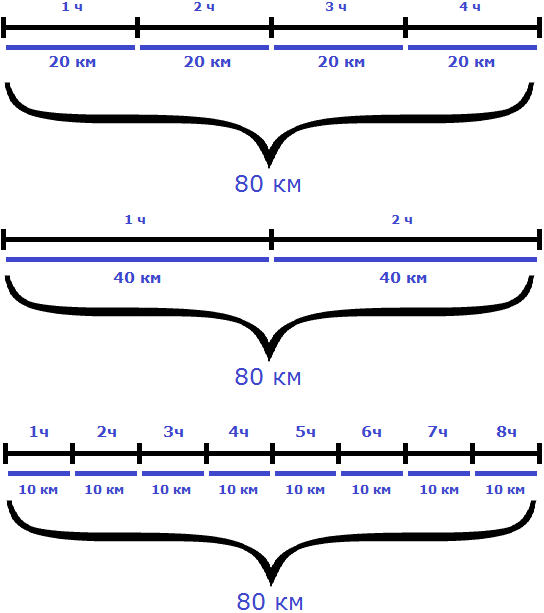
В рассмотренном примере расстояние между городами было равно 80 км. При изменении скорости и времени движения мотоциклиста, это расстояние всегда оставалось неизменным
Мотоциклист мог проехать это расстояние со скоростью 20 км/ч за 4 часа, и со скоростью 40 км/ч за 2 часа, и со скоростью 10 км/ч за 8 часов. Во всех случаях произведение скорости и времени было равно 80 км
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
9 thoughts on “Прямая и обратная пропорциональность”
что ценно теория методически верно преподается. очень добрый сайт.
мне теперь всё понятно, большое спасибо сайту
Источник статьи: http://spacemath.xyz/pryamaya_proporcionalnost/
Пропорциональность
Значения, двух каких бы то ни было величин, могут взаимно зависеть друг от друга.
К примеру, площадь квадрата находится в зависимости от длины его стороны, и так же обратно, длина стороны квадрата зависима от его площади.
Две величины, которые по характеру являются взаимно зависимыми, называются пропорциональными, при условии, если отношение их значений будет неизменным.
Общий вес керосина пропорционален его настоящему объему, например:
Следовательно, отношение веса к его объему будет:
Отношение пропорциональных величин, являющихся неизменным, называются коэффициентом пропорциональности. Этот коэффициент пропорциональности указывает, сколько единиц одной взятой величины приходится на одну единицу другой.
Если две отдельные величины пропорциональны, то любая пара таких значений одной величины, будет образовывать пропорцию с парой соответствующих значений другой, выбранных в том же порядке.
Две величины, которые зависят друг от друга так, что при увеличении значения одной из них другая увеличивается в том, же соотношении, называются пропорциональными.
Две величины, которые зависят друг от друга так, что при увеличении одной величины другая в том же отношении будет уменьшаться, называются обратно пропорциональными.
Например, время пробега состава поезда между двумя отдельными станциями обратно пропорционально скорости этого поезда.
При скорости 50 км/час поезд покрывает расстояние между Москвой и Петербургом за 13 часов, а при скорости 65 км/час – в 10 часов другими словами, когда скорость возростает в отношении 65 / 50 = 13 / 10 , продолжительность пробега уменьшается в том же соотношении:
Если две, какие либо величины являются обратно пропорциональными, то любая пара значений одной величины формирует пропорцию с парой соответствующих значений величин другой, выбранных в обратном порядке, например:
Произведение значений двух обратно пропорциональных величин остаются неизменными.
Источник статьи: http://simple-math.ru/arithmetics/proportionality.php
Пропорциональность
Пропорциональными называются две взаимно зависимые величины, если отношение их значений остаётся неизменным [1] .
Равенство между отношениями двух или нескольких пар чисел или величин в математике называется пропорцией.
Содержание
Пример
Масса керосина пропорциональна его объёму: 2 л керосина имеют массу 1,6 кг, 5 л имеют массу 4 кг, 7 л имеют массу 5,6 кг. Отношение массы к объёму всегда будет равно плотности:
Коэффициент пропорциональности
Неизменное отношение пропорциональных величин называется коэффициентом пропорциональности. Коэффициент пропорциональности показывает, сколько единиц одной величины приходится на единицу другой [1] .
Символ
Математический символ ‘∝’ используется для указания пропорциональности двух величин. Пример, A ∝ B.
В Юникоде для отображения используется символ U+221D.
Прямо пропорциональные величины
Две величины называются прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз, другая увеличивается (уменьшается) во столько же раз. Пример: такие величины, как скорость объекта и пройденное им расстояние являются прямо пропорциональными.
Обратная пропорциональность
Обра́тная пропорциона́льность — это функциональная зависимость, при которой увеличение независимой величины (аргумента) вызывает пропорциональное уменьшение зависимой величины (функции).
- Область определения D ( y ) = ( − ∞ ; 0 ) ∪ ( 0 ; + ∞ ) <\displaystyle D(y)=(-\infty ;0)\cup (0;+\infty )>
- Область значений E ( y ) = ( − ∞ ; 0 ) ∪ ( 0 ; + ∞ ) <\displaystyle E(y)=(-\infty ;0)\cup (0;+\infty )>
- Функция нечётна, так как f ( − x ) = k − x = − k x = − f ( x ) <\displaystyle f(-x)=<\frac
<-x>>=-<\frac >=-f(x)> - Функция убывает на каждом из множеств ( − ∞ ; 0 ) <\displaystyle (-\infty ;0)>
и ( 0 ; + ∞ ) <\displaystyle (0;+\infty )>
по отдельности для 0>»> k > 0 <\displaystyle k>0>
0″/> и возрастает на каждом из них по отдельности при k 0 <\displaystyle k
.
- Графиком обратной пропорциональности является гипербола с эксцентриситетом 2 <\displaystyle <\sqrt <2>>>
.
См. также
Источники
Что такое wiki2.info Вики является главным информационным ресурсом в интернете. Она открыта для любого пользователя. Вики это библиотека, которая является общественной и многоязычной.
Основа этой страницы находится в Википедии. Текст доступен по лицензии CC BY-SA 3.0 Unported License.
Wikipedia® — зарегистрированный товарный знак организации Wikimedia Foundation, Inc. wiki2.info является независимой компанией и не аффилирована с Фондом Викимедиа (Wikimedia Foundation).
Источник статьи: http://wiki2.info/%D0%9F%D1%80%D0%BE%D0%BF%D0%BE%D1%80%D1%86%D0%B8%D0%BE%D0%BD%D0%B0%D0%BB%D1%8C%D0%BD%D0%BE%D1%81%D1%82%D1%8C
Какие есть математические символы?
К самым распространённым относятся:
Что обозначает этот знак ))))) в переписке?
Скобочки в переписках обозначают степень улыбки пользователя, который их отправляет. То есть одна скобочка это просто «доволен», две чуть больше «доволен», три уже смех и далее подразумевается, что пользователь очень сильно смеётся, но обычно, всё это не работает и скобки ставят просто по привычке.
Как напечатать римские цифры на клавиатуре?
Для написания римских цифр необходимо изменить раскладку клавиатуры на английскую (клавиши alt и shift в левой части клавиатуры необходимо нажать одновременно) и использовать в качестве цифр буквы I (русская клавиша «Ш»), V (русская клавиша «М»), X (русская клавиша «Ч»), M (русская клавиша «Ь»).
Какие числа называют целыми?
Целые числа это — множество натуральных чисел (1,2,3,4. n); чисел, противоположных натуральным (-1,-2,-3,-4. -n) и ноль (0).
Иными словами, это числа, не имеющие дробную часть.
Например:
24; 68; 4512; 25687 — все целые (все натуральные числа)
35; -98; 0; -645; 8830 — все целые ( натуральные только 35 и 8830)
654,25; 0,78; -656,4587 — все нецелые (натуральных нет)
Чему равно число Пи?
Никто не знает точно, чему равно пи. Если разделить длину окружности на ее диаметр, то результат всегда будет одинаковый, какую окружность ни возьми. Этот результат и обозначили греческой буквой пи. Буква понадобилась потому, что привычными цифрами это число точно записать невозможно. Но мы знаем, чему оно равно приблизительно.
Самое знаменитое приближение – 3,14. Чтобы запомнить больше цифр, можно выучить стишок:
Источник статьи: http://yandex.ru/q/question/hw.math/kakie_est_matematicheskie_simvoly_361b186d/