Как пишется в паскале логарифм

Как пишется в паскале логарифм

Pers.narod.ru. Алгоритмы. Некоторые математические расчёты на Паскале

Как известно, ядро Паскаля предельно компактно, и многие математические функции в модуле System просто отсутствуют. Поэтому у людей, изучающих основы программирования именно на этом языке, типовые математические расчёты зачастую вызывают проблемы. Далее приводятся пути решения наиболее типичных из этих проблем.

Возведение в произвольную степень на Паскале

Требуется вычислить значение с = a b . В зависимости от значений основания a и показателя степени b , вычисление степени может быть реализовано по-разному.

Если a > 0 , а b может принимать произвольные вещественные значения, используем известную формулу a b = exp (b * ln a) :

Если b — целое число (вообще говоря, «не слишком большое» по модулю), а a — любое (не равное нулю при b ), возведение в степень может быть реализовано с помощью цикла:

Для целого b и не равного нулю a выгоднее считать с помощью экспоненты и логарифма, не забывая о том, что не существует логарифмов от отрицательных чисел:

Вычисление корня произвольной степени на Паскале

Стандартная функция sqrt умеет извлекать только квадратный корень.

Извлечь корень степени n (где n — натуральное) из числа a можно всегда, кроме случая, когда a и при этом n четно. Извлечь корень степени n из числа a означает возвести число a в степень 1/n . При этом знак корня совпадает со знаком a . Ниже приводится код функции, вычисляющей корень произвольной степени n от своего аргумента a :

Вычисление логарифмов на Паскале

Стандартная функция ln вычисляет только натуральный логарифм. Для вычисления логарифмов по другим основаниям можно применить формулу log _a b = ln b / ln a :

В частности, для вычисления десятичного логарифма lg b можно записать:

Вычисление обратных тригонометрических функций (арксинусов и арккосинусов) на Паскале

В Паскале имеется стандартная функция arctan для вычисления арктангенса.

Другие обратные тригонометрические функции могут быть выражены через неё с помощью формул тригонометрии.

Для вычисления y = arcsin x , где, конечно, |x| , можно применить один из следующих способов:

на практике следует помнить о возможных погрешностях при сравнении вещественных чисел (глава учебника, п.7.2).

Для вычисления z = arccos x , где |x| , можно использовать тот факт, что сумма арксинуса и арккосинуса некоторого значения равна прямому углу:

Вычисление полярных углов на Паскале

Полярным углом точки с координатами (x,y) , отличной от начала координат, называют угол между положительным направлением оси Ox и направлением из начала координат на данную точку. При этом угол отсчитывается против часовой стрелки. Строго говоря, полярный угол не всегда равен arctg (y/x) , это верно лишь при x > 0 . Кроме того, при делении большого значения y на малое x возможно переполнение. Показанная ниже функция вычисляет полярный угол fi , лежащий в промежутке от -pi до +pi , для любой точки с координатами (x,y) , не совпадающей с началом координат:

Проблема с приведением типов на Паскале

Начинающие «паскалисты» нередко не понимают строгой типизированности этого языка, из-за чего находят в нём несуществующие «баги». Вот простейший пример.

Эта программа выдаст отнюдь не 200000, как может показаться. Ответ будет равен 3392 (результат переполнения). Никакого бага нет. Тип выражения в Паскале определяется только типом входящих в него переменных, но не типом переменной, куда записывается результат. То есть, мы вычислили с переполнением произведение двух переменных типа Integer , а потом «испорченный» результат переписали в переменную типа Longint . ничего не изменит и

Здесь тоже сначала вычислен результат с переполнением, затем преобразован к типу Longint . А вот

рулит, получите свои 200000 🙂 Указанная ошибка часто встречается в программах начинающих. Чтобы её не повторять, помните — выражение в Паскале должно быть приведено к нужному типу в процессе его вычисления, а не после его окончания или при присваивании.

Источник статьи: http://pers.narod.ru/algorithms/pas_math.html

Функция Ln

Функция Ln вычисляет натуральный логарифм. Для подзабывших математику о логарифмах расскажу чуть позже. А пока синтаксис:

function Ln(Х : ValReal) : ValReal;

Функция Ln X возвращает натуральный логарифм вещественного числа Х. Число Х должно быть положительным — иначе случится ошибка времени выполнения. Хотя в моём случае ошибка не возникает, просто функция возвращает результат “минус бесконечность”. Видимо, это зависит от настроек компилятора.

О типе ValReal я рассказывал здесь.

Подробности см. в видео и читайте в статье далее.

А теперь немного математики.

Сначала вспомним, что такое логарифм.

Логарифм числа b по основанию a определяется как показатель степени, в которую надо возвести основание a, чтобы получить число b. Обозначение:

То есть, чтобы вычислить логарифм числа b по основанию a, надо решить уравнение

где а и b известны, а х — неизвестная величина.

так как число 3 в степени 2 равно 9:

3 2 = 9

Теперь о натуральном логарифме, который и вычисляет функция Ln в Паскале.

Натуральный логарифм — это логарифм по основанию е. Где е — это иррациональная константа, которая равна приблизительно 2,72. То есть

В FreePascal также есть другие функции для вычисления логарифмов:

• Log10 — вычисляет логарифм по основанию 10
• Log2 — вычисляет логарифм по основанию 2
• LogN — вычисляет логарифм по основанию N (в эту функцию передаются два параметра, сначала — основание N, затем число X)
• Lnxp1 — вычисляет натуральный логарифм по основанию Х+1

Но эти функции определены в модуле Math. То есть, чтобы воспользоваться этими функциями вам придётся подключить модуль Math к своей программе.

Такие вещи как область определения натурального логарифма Ln, производная, разложение в ряд Тейлора и прочие “ништяки” рассматривать не будем, так как это уже далеко выходит за сферу программирования.

А вот формулу, которая позволяет вычислить логарифм по произвольному основанию, используя только функцию Ln, я вам покажу:

То есть, если вы не хотите подключать к вашей программе модуль Math, то это вам не помешает вычислить логарифм с любым основанием.

Пример собственной функции, которая является аналогом функции LogN из модуля Math, вы найдёте в исходном коде ниже.

Источник статьи: http://info-master.su/programming/pascal-functions/ln.php

Десятичный логарифм

Как правильно записать функцию десятичного логарифма y=lg(x+6)? Помогите пожалуйста.

Добавлено через 16 минут
Все, не надо, я вспомнила)))

Десятичный логарифм
как правильно записать функцию десятичного логарифма lg(x+5)=cosx

Десятичный логарифм, функции
Вычислить значение выражения с помощью функции.

Вычислить логарифм
Как записать в паскале lg(j-i) и e^2j Cпасибо.

Вычислить логарифм
Помогите пожалуйста. Как записать пример?

Решение

Заказываю контрольные, курсовые, дипломные и любые другие студенческие работы здесь.

Функция не считает логарифм
Не пойму почему функция считает не правильно логарифм: function ln(a : real) : real; .

Если частное чисел — четное, то вычислить логарифм
как сделать программу?

Вычислить логарифм как сумму знакопеременного ряда
http://i.pixs.ru/thumbs/9/5/7/Bezimyanni_6323477_6088957.jpg Если можно, то с комментариями))).

Логарифм
program one; //uses crt; var x1, x2, x3, y1, y2, y3: real; begin //clrscr; .

Источник статьи: http://www.cyberforum.ru/turbo-pascal/thread686812.html

Уроки Паскаль

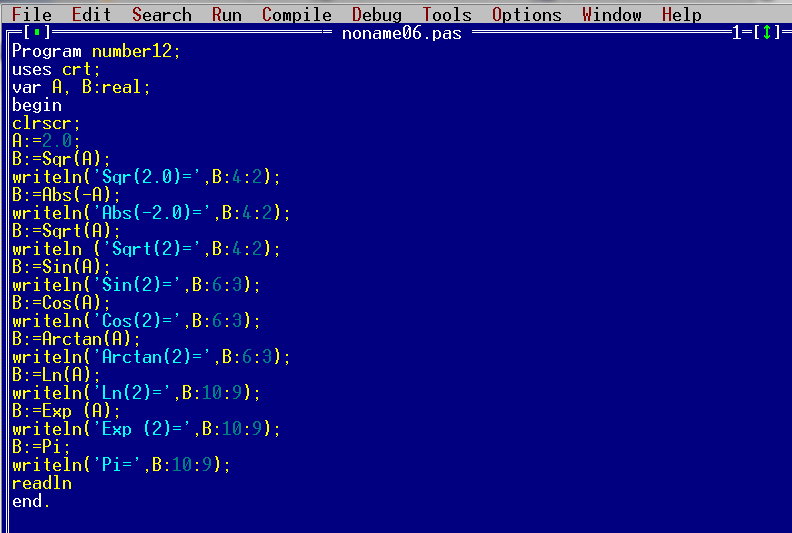
Мы уже знаем, какие существуют функции для целых переменных. Это – нахождение модуля числа (Функция Abc), а также возведение числа в квадрат (Функция Sqr). В этом уроке мы рассмотрим функции, применяемые к дробным числам. Это функции Sqr — квадрат числа, Abs — модуль числа, Sqrt — корень числа, а также известные всем математические функции Sin, Cos, Arctan, Ln, Exp, Pi.

В строке №7 записывается функция Sqr. Это функция возведения числа в квадрат.

В строке №9 записывается операция нахождения модуля числа.
Функции Sqr и Abs мы разбирали в уроке Abs, Sqr в Pascal.

В строке №11 записывается функция Sqrt. Данная функция подсчитывает корень числа, стоящего в скобках после слова Sqrt. В нашем случае функция Sqrt будет считать корень из числа «2».

В строке №13 записываем функцию Sin. Данная функция будет подсчитывать синус числа, стоящего в скобках после записи функции.

Строка №15. Функция Cos подсчитывает косинус числа, стоящего в скобках после функции.

Строка №17. Функция Arctan вычисляет арктангенс числа, стоящего в скобках после записи функции.

Строка №19. Функция Ln подсчитывает логарифм числа, стоящего в скобках после записи функции.

Строка №21. Функция Exp возводит число «e» (экспонента — 2.72. ) в степень, значение которой указывается в скобках после слова Exp. Т.е. в нашем случае число «e» будет возведено в степень «2».

Строка №23. Переменной «B» будет присвоено значение числа «?».

Дополнение к материалу.

• Функции Sqrt, Sin, Cos, Arctan, Ln, Exp, Pi определены только для вещественных (дробных) чисел.
• В Паскале не существует операции возведения в степень. Есть только операция возведения числа в квадрат (Sqr). Чтобы возвести число в степень используют операцию умножения. Например, чтобы возвести число 3 в 5-ю степень необходимо записать 3*3*3*3*3

Источник статьи: http://mojainformatika.ru/paskal/uroki-paskal/14-ispolzovanie-sqr-abs-sqrt-sin-cos-arctan-ln-exp-pi.html