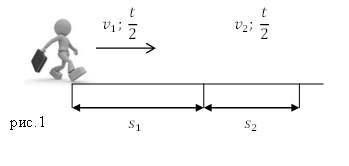
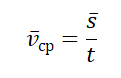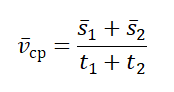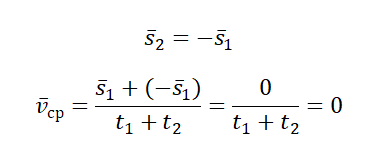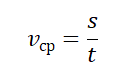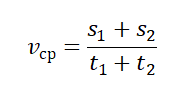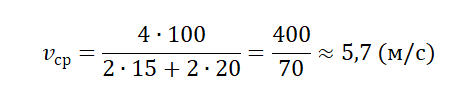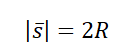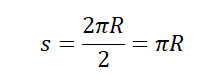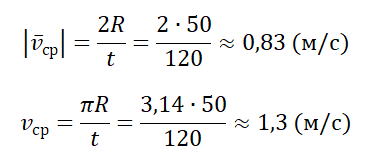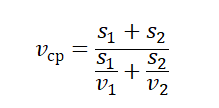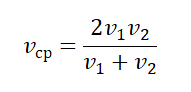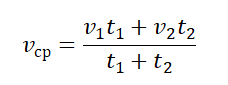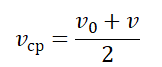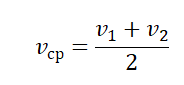Формула средней скорости
Средняя скорость тела — это отношение пути к времени прохождения этого пути. Скорость движения не требуется постоянной.
Здесь — средняя скорость, — весь путь, пройденный телом, — время прохождения пути.
Единица измерения скорости — м / с (метр в секунду).
Средняя скорость — это скаляр. Если тело перемещается с разной скоростью в равные промежутки времени, то средняя скорость равна среднему арифметическому для всех скоростей, в противном случае
Где — отрезок пути, — время прохождения этого отрезка.
Примеры решения проблем на тему «Средняя скорость»
Тело прошло 5 метров за 12 секунд, затем 7 метров за 3 секунды. Найдите среднюю скорость тела.
Решение очевидно (S и t — путь и время прохождения этого пути для определенных сегментов):
Средняя скорость тела равна метров в секунду.
Средняя скорость движения тела . Скорость на первой секции была , на второй , на третьей длине секций S1, S2 и S3 соответственно. Мы не знаем S2. Найдите время прохождения второго раздела.
Давайте рассмотрим формулу средней скорости для трех разделов:
В этой форме формула ничего нам не дает, но если вспомнить, что
Источник статьи: http://sciterm.ru/spravochnik/formula-srednej-skorosti/
Средняя скорость
Перемещение материальной точки
Пусть материальная точка совершает движение по оси X все время в одном направлении. Тогда перемещением этой материальной точки за отрезок времени $\Delta t=t_2-t_1$ будет отрезок $\Delta x=x_2-x_1$. Если материальная точка все время своего движения перемещалась в одном направлении, то пройденный путь ($\Delta s$) равен по модулю величине перемещения:
\[\Delta s=\left|\Delta x\right|\left(1\right).\]
Если точка движется сначала в одном направлении, затем останавливается и движется в противоположном направлении, (например, так движется тело брошенное вертикально вверх) то путь равен сумме модулей перемещений в обоих направлениях:
\[\Delta s=\left|\Delta x_1\right|+\left|\Delta x_2\right|+\dots \left(2\right).\]
Определение средней скорости
Средней скоростью ($\left\langle v\right\rangle $) материальной точки за промежуток времени $\Delta t$ называют физическую величину, которая равна отношению перемещения, которое совершило тело к этому промежутку времени:
\[\left\langle v\right\rangle =\frac<\Delta x><\Delta t>\left(3\right).\]
Направление средней скорости такое же, как у перемещения.
Единицей скорости является скорость такого движения, при котором перемещение точки в единицу времени равно единице длины:
Единица измерения скорости (в том числе и средней скорости) в Международной системе единиц (СИ) является метр в секунду:
Средняя скорость при переменном движении
При неравномерном движении величина средней скорости сильно зависит от выбора промежутка времени движения тела.
Рассмотрим движение тела, которое свободно падает вниз. Закон движения при этом:
Для моментов времени $t_1=0,1\ $c координата тела (подставим время $t_1$ в формулу (4)) равна: $x_1=0,049\ $м; для $t_2=0,2\ $c$\ x_2=0,196$ м, тогда $\left\langle v\right\rangle $в промежутке времени от $t_1=0,1$ с до $t_2=0,2\ $c будет:
Если взять для того же свободно падающего тела промежуток времени от $t_1=0,7$ с до $t_2=0,8\ $c, то средняя скорость получится равной $\left\langle v\right\rangle =7,4\frac<м><с>$.
Средняя скорость равномерного движения
Только при равномерном движении средняя скорость является постоянной величиной и не зависит от выбора промежутка времени, в который движется тело. При равномерном движении материальной точки по оси X кинематические уравнения для перемещения запишем как:
Найдем среднюю скорость движения, используя определение (3) и выражения (6):
Для оценки численной величины средней скорости на практике используют следующее определение $\left\langle v\right\rangle $: средняя скорость равна отношению пройдённого пути (s) ко времени (t), которое было затрачено на движение:
\[\left\langle v\right\rangle =\frac Определяемая таким образом средняя скорость является скалярной величиной. Задание. Пешеход, потратил первую половину времени своего движения, двигаясь со скоростью $v_1=5\frac<км><ч>$, вторую половину времени он шел со скоростью $v_3=3\frac<км><ч>$. Какова средняя скорость движения человека? Решение. Сделаем рисунок. Для решения задачи используем формулу, определяющую среднюю скорость: \[\left\langle v\right\rangle =\frac где путь складывается из двух участков движения: Причем по условию задачи: \[s_1=v_1t_1=v_1\frac Подставим в определение средней скорости (1.1) правые части выражений (1.2) — (1.4), и учтем, что $t=t_1+t_2$ имеем: Вычислим среднюю скорость пешехода: \[\left\langle v\right\rangle =\frac<5+3><2>=4\ (\frac<м><с>).\] Ответ. $\left\langle v\right\rangle =4\frac<м><с>$ Задание. Какова средняя скорость, которую имела материальная точка за промежуток времени $\tau $, если уравнение ее скорости имеет вид: \[v\left(t\right)=A+Bt+Ct^2\ \left(0\le t\le \tau \right)\left(2.1\right).\] Решение. В качестве основы для решения задачи используем формулу ($t=\tau $): \[\left\langle v\right\rangle =\frac Найдем путь материальной точки, учитывая уравнение скорости из данных задачи: Подставим правую часть выражения (2.2) в (2.1), имеем: Ответ. $\left\langle v\right\rangle =A+\frac Источник статьи: http://www.webmath.ru/poleznoe/fizika/fizika_33_srednjaja_skorost.php Неравномерное движение — движение с переменной скоростью, которая может менять как направление, так и модуль. Неравномерное движение можно охарактеризовать средней скоростью. Различают среднюю векторную и среднюю скалярную скорости. Средняя векторная скорость — это скорость, равная отношению перемещения тела ко времени, в течение которого это перемещение было совершено. v ср — средняя векторная скорость, s — перемещение тела, совершенное за время t Направление вектора средней скорости всегда совпадает с направлением вектора перемещения. Чтобы вычислить среднюю векторную скорость, нужно поделить сумму всех перемещений на сумму всех временных промежутков, в течение которых эти перемещения были совершены: Пример №1. Миша пробежал стометровку за 16 секунд. Через 1 минуту он вернулся на старт. Найти среднюю векторную скорость мальчика. Миша совершил одинаковые по модулю, но разные по направлению перемещения. При сложении этих векторов получается 0. Поэтому средняя векторная скорость также равна нулю: Средняя скалярная (путевая) скорость — это скорость, равная отношению пути, пройденного телом, ко времени, в течение которого этот путь был пройден. vср — средняя путевая скорость, s — путь, пройденный телом за время t Чтобы вычислить среднюю путевую скорость, нужно поделить сумму всех путей на сумму всех временных промежутков, в течение которых эти пути были преодолены: Пример №2. Мальчик пробежал по периметру квадратного поля сто стороной 100 м. На первые две стороны мальчик потратил по 15 секунд, а на последние две — по 20 секунд. Найти среднюю путевую скорость мальчика. У квадрата 4 стороны, поэтому путь мальчика составляют 4 дистанции по 100 м каждая. Поэтому средняя путевая скорость равна: Средняя скалярная скорость всегда больше или равна модулю средней векторной скорости: Пример №3. Рыболов остановился на берегу круглого пруда и увидел на противоположном берегу удобное для рыбалки место. Он к нему шел в течение 2 минут. Вычислите среднюю путевую и среднюю векторную скорости рыболова после того, как он придет на новое место, если радиус пруда равен 50 м. Две противоположные точки окружности соединяются отрезком, проходящим через его центр — диаметром. Поэтому модуль вектора перемещения равен двум радиусам пруда: Чтобы дойти до диаметрально противоположной точки окружности, нужно пройти путь, равный половине окружности: Переведя 2 минуты в СИ, получим 120 с. Модуль средней векторно скорости равен: Пример №4. Первые полчаса автомобиль двигался со скоростью 90 км/ч, а потом 1 час он двигался со скоростью 60 км/ч. Найти среднюю скорость автомобиля. Нам известны скорости на каждом из участков пути и время, в течение которого каждый из этих участков был преодолен. Поэтому: Источник статьи: http://spadilo.ru/neravnomernoe-dvizhenie-i-srednyaya-skorost/Примеры задач с решением
СПАДИЛО.РУ
теория по физике 🧲 кинематика
Средняя векторная скорость
Средняя скалярная скорость