Как найти разность чисел в математике
- Арифметические действия с числами
- Разность в математике
- Как найти разницу величин
- Математические действия с разностью чисел
- Простые примеры
- Более сложные примеры
- Математика для блондинок
Арифметические действия с числами
Основными арифметическими действиями в математике являются:
Каждый результат этих действий также имеет своё название:
- сумма — результат, получившийся при сложении чисел,
- разность — результат, получившийся при вычитании чисел,
- произведение — результат умножения чисел,
- частное — результат деления.
Это интересно: что такое модуль числа?
Более простым языком объясняя понятия суммы, разности, произведения и частного в математике, можно упрощённо записать их лишь как словосочетания:
- сумма — прибавить,
- разность — отнять,
- произведение — умножить,
- частное — разделить.
Разность в математике
Рассматривая определения, что же такое разность чисел в математике, можно обозначить это понятие несколькими способами:
Разность чисел означает, насколько одно из них больше другого.
- Разностью в математике называется итог, получившийся при отнимании друг от друга двух и более чисел.
- Это вычитание одного числа из другого.
- Это цифра, составляющая остаток при минусовании двух величин.
- Это величина, являющаяся результатом вычитания двух значений.
- Разность показывает количественное различие между двумя цифрами.
- Это результат одного из четырёх арифметических действий, которым является вычитание.
- Это то, что получится, если из уменьшаемого отнять вычитаемое.
И все эти определения являются верными.
Как найти разницу величин
Возьмём за основу то обозначение разности, которое нам предлагает школьная программа:
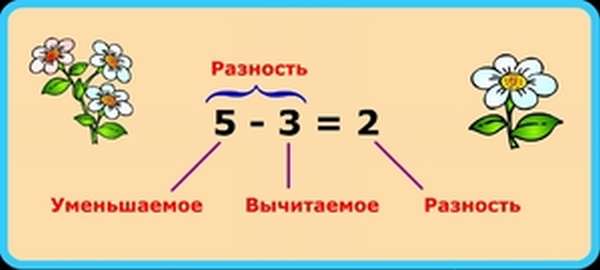
- Разностью называется результат вычитания одного числа из другого. Первое из этих чисел, из которого осуществляется вычитание, называется уменьшаемым, а второе, которое вычитают из первого, называется вычитаемым.
Ещё раз прибегнув к школьной программе, мы находим правило, как найти разность:
- Чтобы найти разность, надо от уменьшаемого отнять вычитаемое.
Всё понятно. Но при этом мы получили ещё несколько математических терминов. Что они значат?
- Уменьшаемое — это математическое число, от которого отнимают и оно уменьшается (становится меньше).
- Вычитаемое — это математическое число, которое вычитают из уменьшаемого.
Теперь понятно, что разность состоит из двух чисел, которые для её вычисления должны быть известны. А как их найти тоже воспользуемся определениями:
- Чтобы найти уменьшаемое, надо к вычитаемому прибавить разность.
- Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность.
Математические действия с разностью чисел
Опираясь на выведенные правила, можно рассмотреть наглядные примеры. Математика, интереснейшая наука. Мы здесь возьмём для решения лишь самые простые цифры. Научившись вычитать их, вы научитесь решать и более сложные значения, трёхзначные, четырёхзначные, целые, дробные, в степенях, корнях, другие.
Простые примеры
- Пример 2. Найти уменьшаемое.
- Пример 3. Найти вычитаемое значение.
Ответ: вычитаемое значение 10.
Более сложные примеры
На примерах 1—3 рассмотрены действия с простыми целыми числами. Но в математике разницу вычисляют с применением не только двух, но и нескольких чисел, а также целых, дробных, рациональных, иррациональных, др.
- Пример 4. Найти разницу трёх значений.
12 и 4 — вычитаемые значения.
Решение можно выполнить двумя способами.
1 способ (последовательное отнимание вычитаемых значений):
1) 56 — 12 = 44 (здесь 44 — получившаяся разница двух первых величин, которая во втором действии будет уменьшаемым),
2 способ (отнимание из уменьшаемого суммы двух вычитаемых, которые в таком случае называются слагаемыми):
1) 12 + 4 = 16 (где 16 — сумма двух слагаемых, которая в следующем действии будет вычитаемым),
Ответ: 40 — разница трёх значений.
- Пример 5. Найти разницу рациональных дробных чисел.
Даны дроби с одинаковыми знаменателями, где
Чтобы выполнить решение, нужно повторить действия с дробями. То есть, надо знать как отнимать дроби с одинаковым знаменателем. Как обращаться с дробями, имеющими разные знаменатели. Их надо уметь привести к общему знаменателю.
Решение: 4/5 — 3/5 = (4 — 3)/5 = 1/5
- Пример 6. Утроить разницу чисел.
А как выполнить такой пример, когда требуется удвоить или утроить разницу?
Вновь прибегнем к правилам:
- Удвоенное число — это величина, умноженная на два.
- Утроенное число — это величина, умноженная на три.
- Удвоенная разность — это разница величин, умноженная на два.
- Утроенная разность — это разница величин, умноженная на три.
2) 2 * 3 = 6. Ответ: 6 — разница чисел 7 и 5.
- Пример 7. Найти разницу величин 7 и 18.
Вроде всё понятно. Стоп! Вычитаемое больше уменьшаемого?
И опять есть применяемое для конкретного случая правило:
- Если вычитаемое больше уменьшаемого, разница окажется отрицательной.
Ответ: — 11. Это отрицательное значение и есть разница двух величин, при условии, что вычитаемая величина больше уменьшаемой.
Математика для блондинок
В школе подобные действия с математическими величинами нас учили вычислять в столбик, а позднее — на калькуляторе. Калькулятор — это также удобное подспорье. Но, для развития мышления, интеллекта, кругозора и других жизненных качеств, советуем производить арифметические действия на бумаге или даже в уме. Красота человеческого тела — это великое достижение современного фитнес-плана. Но мозг — это тоже мышца, которая требует иногда её качать. А значит, не откладывая, начинайте думать.
И пусть в начале пути вычисления сводятся к примитивным примерам, всё у вас впереди. А освоить придётся немало. Мы видим, что действий с разными величинами в математике множество. Поэтому кроме разницы необходимо изучить, как вычислить и остальные результаты арифметических действий:
- сумму — сложением слагаемых,
- произведение — умножением множителей,
- частное — делением делимого на делитель.
Источник статьи: http://tvercult.ru/nauka/kak-nayti-raznost-chisel-v-matematike
Какие есть математические символы?
К самым распространённым относятся:
Что обозначает этот знак ))))) в переписке?
Скобочки в переписках обозначают степень улыбки пользователя, который их отправляет. То есть одна скобочка это просто «доволен», две чуть больше «доволен», три уже смех и далее подразумевается, что пользователь очень сильно смеётся, но обычно, всё это не работает и скобки ставят просто по привычке.
Какие интересные логические и математические парадоксы вы знаете? Можете ли вы их объяснить «на пальцах»?
Каждое второе натуральное число делится на два, каждое третье-на три, каждое четвертое-на четыре. Казалось бы царит полная гармония. Но откуда берется беспорядок с простыми числами(которые делятся сами на себя и единицу)? Вот почему говорят, что хаос это непознанная закономерность.
Чему равно число Пи?
Никто не знает точно, чему равно пи. Если разделить длину окружности на ее диаметр, то результат всегда будет одинаковый, какую окружность ни возьми. Этот результат и обозначили греческой буквой пи. Буква понадобилась потому, что привычными цифрами это число точно записать невозможно. Но мы знаем, чему оно равно приблизительно.
Самое знаменитое приближение – 3,14. Чтобы запомнить больше цифр, можно выучить стишок:
Три, четырнадцать, пятнадцать,
Как напечатать римские цифры на клавиатуре?
Для написания римских цифр необходимо изменить раскладку клавиатуры на английскую (клавиши alt и shift в левой части клавиатуры необходимо нажать одновременно) и использовать в качестве цифр буквы I (русская клавиша «Ш»), V (русская клавиша «М»), X (русская клавиша «Ч»), M (русская клавиша «Ь»).
Какой математический факт вас поражает больше всего?
Математика — обширна, в ней паралельно существуют совершенно разные науки. Уже в школе математика, начинаясь с основ арифметики и операций с натуральными числами, позже делится на алгебру и геометрию. В университете появляется математический анализ, аналитическая геометрия, комплексный анализ. А есть еще функциональный анализ, динамические системы, топология, теория кос, алгебры Ли, итд.
Но оказывается, что все разделы математики тесно связаны между собой. Например, есть такой математический факт:
В этой формуле соединены 5 фундаментальных математических констант из разных наук:
- 0 — «единичный элемент» в группе действительных чисел по сложению (арифметика)
- 1 — «единичный элемент» в поле действительных чисел по умножению (теория чисел)
- e — основание натуральных логарифмов, производная функции e^x равна самой себе (матанализ)
- pi — отношение длины окружности к ее диаметру (геометрия)
- i — «мнимая единица», основа комплексных чисел (комлексный анализ)
Источник статьи: http://yandex.ru/q/question/hw.math/kakie_est_matematicheskie_simvoly_361b186d/
Как найти разность чисел в математике

Арифметические действия с числами
Основными арифметическими действиями в математике являются:
Каждый результат этих действий также имеет своё название:
- сумма — результат, получившийся при сложении чисел;
- разность — результат, получившийся при вычитании чисел;
- произведение — результат умножения чисел;
- частное — результат деления.
Более простым языком объясняя понятия суммы, разности, произведения и частного в математике, можно упрощённо записать их лишь как словосочетания:
- сумма — прибавить;
- разность — отнять;
- произведение — умножить;
- частное — разделить.
Разность в математике
Рассматривая определения, что же такое разность чисел в математике, можно обозначить это понятие несколькими способами:
Разность чисел означает, насколько одно из них больше другого.
- Разностью в математике называется итог, получившийся при отнимании друг от друга двух и более чисел.
- Это вычитание одного числа из другого.
- Это цифра, составляющая остаток при минусовании двух величин.
- Это величина, являющаяся результатом вычитания двух значений.
- Разность показывает количественное различие между двумя цифрами.
- Это результат одного из четырёх арифметических действий, которым является вычитание.
- Это то, что получится, если из уменьшаемого отнять вычитаемое.
Видео: Математика 6 Делимость суммы и разности чисел
И все эти определения являются верными.
Как найти разницу величин
Возьмём за основу то обозначение разности, которое нам предлагает школьная программа:
- Разностью называется результат вычитания одного числа из другого. Первое из этих чисел, из которого осуществляется вычитание, называется уменьшаемым, а второе, которое вычитают из первого, называется вычитаемым.
Ещё раз прибегнув к школьной программе, мы находим правило, как найти разность:
- Чтобы найти разность, надо от уменьшаемого отнять вычитаемое.
Всё понятно. Но при этом мы получили ещё несколько математических терминов. Что они значат?
- Уменьшаемое — это математическое число, от которого отнимают и оно уменьшается (становится меньше).
- Вычитаемое — это математическое число, которое вычитают из уменьшаемого.
Теперь понятно, что разность состоит из двух чисел, которые для её вычисления должны быть известны. А как их найти тоже воспользуемся определениями:
- Чтобы найти уменьшаемое, надо к вычитаемому прибавить разность.
- Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность.
Математические действия с разностью чисел
Опираясь на выведенные правила, можно рассмотреть наглядные примеры. Математика, интереснейшая наука. Мы здесь возьмём для решения лишь самые простые цифры. Научившись вычитать их, вы научитесь решать и более сложные значения, трёхзначные, четырёхзначные, целые, дробные, в степенях, корнях, другие.
Видео: Математика 2 класс. Разность двухзначных чисел
Простые примеры
- Пример 2. Найти уменьшаемое.
- Пример 3. Найти вычитаемое значение.
Ответ: вычитаемое значение 10.
Более сложные примеры
На примерах 1—3 рассмотрены действия с простыми целыми числами. Но в математике разницу вычисляют с применением не только двух, но и нескольких чисел, а также целых, дробных, рациональных, иррациональных, др.
- Пример 4. Найти разницу трёх значений.

12 и 4 — вычитаемые значения.
Решение можно выполнить двумя способами.
1 способ (последовательное отнимание вычитаемых значений):
1) 56 — 12 = 44 (здесь 44 — получившаяся разница двух первых величин, которая во втором действии будет уменьшаемым);
2 способ (отнимание из уменьшаемого суммы двух вычитаемых, которые в таком случае называются слагаемыми):
1) 12 + 4 = 16 (где 16 — сумма двух слагаемых, которая в следующем действии будет вычитаемым);
Ответ: 40 — разница трёх значений.
- Пример 5. Найти разницу рациональных дробных чисел.
Даны дроби с одинаковыми знаменателями, где
Чтобы выполнить решение, нужно повторить действия с дробями. То есть, надо знать как отнимать дроби с одинаковым знаменателем. Как обращаться с дробями, имеющими разные знаменатели. Их надо уметь привести к общему знаменателю.
Решение: 4/5 — 3/5 = (4 — 3)/5 = 1/5
- Пример 6. Утроить разницу чисел.
А как выполнить такой пример, когда требуется удвоить или утроить разницу?
Вновь прибегнем к правилам:
- Удвоенное число — это величина, умноженная на два.
- Утроенное число — это величина, умноженная на три.
- Удвоенная разность — это разница величин, умноженная на два.
- Утроенная разность — это разница величин, умноженная на три.
2) 2 * 3 = 6. Ответ: 6 — разница чисел 7 и 5.
- Пример 7. Найти разницу величин 7 и 18.
Вроде всё понятно. Стоп! Вычитаемое больше уменьшаемого?
И опять есть применяемое для конкретного случая правило:
- Если вычитаемое больше уменьшаемого, разница окажется отрицательной.
Ответ: — 11. Это отрицательное значение и есть разница двух величин, при условии, что вычитаемая величина больше уменьшаемой.
Математика для блондинок

В школе подобные действия с математическими величинами нас учили вычислять в столбик, а позднее — на калькуляторе. Калькулятор — это также удобное подспорье. Но, для развития мышления, интеллекта, кругозора и других жизненных качеств, советуем производить арифметические действия на бумаге или даже в уме. Красота человеческого тела — это великое достижение современного фитнес-плана. Но мозг — это тоже мышца, которая требует иногда её качать. А значит, не откладывая, начинайте думать.
И пусть в начале пути вычисления сводятся к примитивным примерам, всё у вас впереди. А освоить придётся немало. Мы видим, что действий с разными величинами в математике множество. Поэтому кроме разницы необходимо изучить, как вычислить и остальные результаты арифметических действий:
- сумму — сложением слагаемых;
- произведение — умножением множителей;
- частное — делением делимого на делитель.
Источник статьи: http://obrazovanie.guru/nauka/matematika/kak-najti-raznost-chisel.html

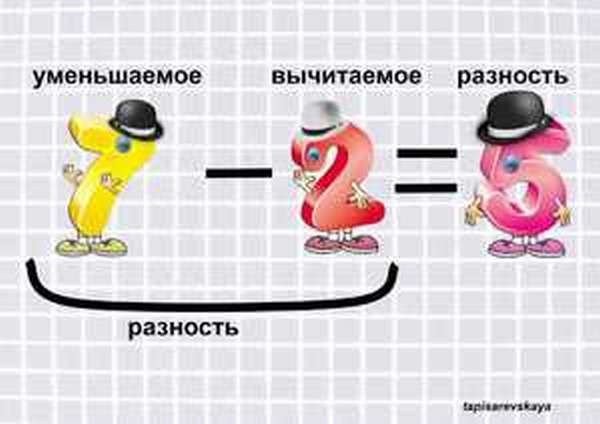 Разность чисел означает, насколько одно из них больше другого.
Разность чисел означает, насколько одно из них больше другого.