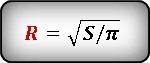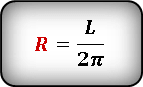Все основные формулы для определения длины радиуса окружности
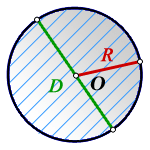
Радиус окружности — отрезок, соединяющий её центр и любую другую точку расположенную на линии окружности.
Окружность это замкнутая кривая линия, все точки которой, равноудалены от другой, определенной точки (центр окружности) на заданном расстоянии (радиус).
R — радиус окружности (круга)
D — диаметр, D = 2 R
Формула для определения длины радиуса, если известна площадь круга :
Калькулятор для расчета длины радиуса через площадь
Формула для определения длины радиуса, если известна длина окружности :
Калькулятор для расчета длины радиуса через длину окружности
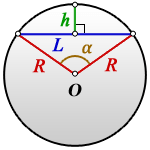
R — радиус окружности (круга)
h — высота сегмента
α — центральный угол
Формула для определения длины радиуса, если известна длина хорды :
Источник статьи: http://www-formula.ru/radius-if-known-area
Нахождение радиуса круга: формула и примеры
В данной публикации мы рассмотрим, как можно вычислить радиус круга (окружности) и разберем примеры решения задач для закрепления материала.
Формулы вычисления радиуса круга
1. Через длину окружности/периметр круга
Радиус круга/окружности рассчитывается по формуле:
C – это длина окружности/периметр круга; равняется удвоенному произведению числа π на его радиус:
C = 2 π R
π – число, приближенное значение которого равно 3,14.
2. Через площадь круга
Радиус круга/окружности вычисляется таким образом:
S – это площадь круга; равна числу π , умноженному на квадрат его радиуса:
S = π R 2
Примеры задач
Задание 1
Длина окружности равняется 87,92 см. Найдите ее радиус.
Решение:
Используем первую формулу (через периметр):
Задание 2
Найдите радиус круга, если его площадь составляет 254,34 см 2 .
Решение:
Воспользуемся формулой, выраженной через площадь фигуры:
Источник статьи: http://microexcel.ru/radius-kruga/
Как найти радиус круга
команда опытных редакторов и исследователей wikiHow
В создании этой статьи участвовала наша опытная команда редакторов и исследователей, которые проверили ее на точность и полноту.
Команда контент-менеджеров wikiHow тщательно следит за работой редакторов, чтобы гарантировать соответствие каждой статьи нашим высоким стандартам качества.
Количество просмотров этой статьи: 639 293.
Радиус круга – это расстояние от центра круга до любой точки, которая лежит на внешней окружности круга. [1] X Источник информации Простейший способ найти радиус – разделить диаметр пополам. Если диаметр не известен, но даны значения других величин, таких как длина окружности ( C = 2 π ( r ) <\displaystyle C=2\pi (r)> 
) или площадь круга ( A = π ( r 2 ) <\displaystyle A=\pi (r^<2>)> ), радиус можно вычислить по специальным формулам, изолировав переменную r <\displaystyle r> . Наконец, если дан центральный угол и площадь сектора круга, можно воспользоваться формулой A = θ 360 ( π ) ( r 2 ) <\displaystyle A=<\frac <\theta ><360>>(\pi )(r^<2>)> , чтобы найти радиус. Обратите внимание, что в данной статье площадь обозначена как A <\displaystyle A> , но в российских учебниках принято обозначение S <\displaystyle S> .
Источник статьи: http://ru.wikihow.com/%D0%BD%D0%B0%D0%B9%D1%82%D0%B8-%D1%80%D0%B0%D0%B4%D0%B8%D1%83%D1%81-%D0%BA%D1%80%D1%83%D0%B3%D0%B0
Длина окружности и площадь круга. Формулы и примеры.
Начнем с того, что определим окружность , как замкнутую плоскую кривую, состоящую из всех точек на плоскости, которые равноудалены от заданной точки. Эта заданная точка является центром окружности . Прямой отрезок, который проходит через центр окружности и соединяет 2 точки на ее границе, называется диаметром . А радиусом будет являться прямой отрезок, которые соединяем точку на границе окружности и ее центр.
Так как окружность – это граница круга, то длина окружности является частным случаем периметра.
Не каждый студент может себе позволить за семестр в ВУЗе отдать 100 000 ₽ . Но круто, что есть гранты на учебу. Грант-на-вуз.рф – это возможность учиться на желанной специальности. По ссылке каждый получит бонус от 300 ₽ до 100 000 ₽ – грант-на-вуз.рф
Длина окружности круга
Множество точек удаленных от центра круга на расстояние, не превышающее радиус круга, называется кругом. Отношение длины любой окружности C к ее диаметру d всегда будет равно одному и тому же числу. Это число – всем известное число π («пи»), которое примерно равно 3,14. Так же, справедлива формула определения числа π , как отношение длины окружности C к двум ее радиусам r . Исходя из этого, выводится формула длины окружности C , которая равна произведения числа π и диаметра d окружности или 2-м ее радиусам r .
Для примера решим простую задачу, где нужно найти длину окружности, у которой известен радиус r =2 см.
Подставляем известные данные в формулу длины окружности и получаем, что длина окружности примерно равна 12,56 см.
Площадь круга
Площадь круга S, как и длина окружности, вычисляется с помощью константы π и радиуса окружности r .
Так же можно получить значение площади S круга с помощью диаметра d .
Источник статьи: http://zen.yandex.ru/media/studystudent/dlina-okrujnosti-i-ploscad-kruga-formuly-i-primery-5e9d7c122517bd2ed0b40460
Знак радиуса
Радиус – лат. radius – спица колеса, луч – отрезок прямой линии соединяющей центр окружности с какой-либо точкой окружности или сферы. При нанесении размеров на чертеже радиус обозначается буквой R , за которой следуют размерные числа.
При необходимости явного указания центра окружности, при нанесении размера радиуса, его изображают в виде пересечения центровых или выносных линий.
Если радиус слишком велик для того чтобы отобразить его на чертеже, центр допускается приближать к дуге, а линию радиуса показывают с изломом под углом 90° .
Нанесение радиуса дуги с приближением к ней центра
Если центр не требуется указывать, то размерную линию радиуса допускается не доводить до центра и смещать ее относительно центра.
Нанесение радиуса дуги, когда не требуется указывать размеры,
определяющие положение её центра
Когда требуется провести несколько радиусов из одного центра, соблюдается условие, при котором размерные линии любых двух радиусов не располагают на одной прямой.
Линии радиуса располагаются на одной прямой
В том случае если из одного центра нужно провести несколько размерных линий радиуса, допускается не доводить их до центра, кроме крайних.
Линии радиуса не доводятся до центра
Для наибольшего удобства чтения чертежа, размерные числа и стрелки наносятся в различных положениях.
Нанесение размеров наружных скруглений
Нанесение размеров внутренних скруглений
Графически радиус не отображают, в том случае, когда размер в масштабе чертежа равен 1мм и менее.
Нанесение радиусов от 1мм и менее
Если часть радиусов скругления одинаковые, размеры допускается указывать на общей полке.
Нанесение одинаковых радиусов скруглений
Если на всём чертеже радиусы скруглений одинаковые или радиус является преобладающим, рекомендуется не наносить размеры, а указывать их в технических требованиях, например: «Радиусы скругления 5 мм»; «Внутренние радиусы сгибов 3мм»; «Неуказанные радиусы 8 мм» и т.п.
Размеры радиуса дуги окружности, которые сопрягаются с параллельными линиями, допускается не наносить.
Источник статьи: http://gk-drawing.ru/plotting/size-radius.php