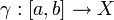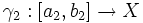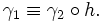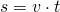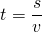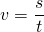Как пишется путь в математике

Как пишется путь в математике

В рамках элементарной геометрии понятие кривой не получает отчётливой формулировки и иногда определяется как «длина без ширины» или как «граница фигуры». По существу в элементарной геометрии изучение кривых сводится к рассмотрению примеров (прямая, отрезок, ломаная, окружность и др.). Не располагая общими методами, элементарная геометрия довольно глубоко проникла в изучение свойств конкретных кривых (конические сечения, некоторые алгебраические кривые высших порядков и также трансцендентные кривые), применяя в каждом случае специальные приёмы.

Параметрические определения

Чаще всего кривая определяется как непрерывное отображение из отрезка в пространство:

При этом, кривые могут быть различными, даже если их образы совпадают. Такие кривые называют параметризованными кривыми или, если [a,b] = [0,1] , путями.

Иногда кривая определяется с точностью до репараметризации, то есть с точностью до минимального отношения эквивалентности такого что параметрические кривые

и

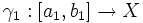
эквивалентны, если существует непрерывная монотонная функция (иногда неубывающая) h из отрезка [a₁,b₁] на отрезок [a₂,b₂] , такая что

Определяемые этим отношением классы эквивалентности называются непараметризованными кривыми или просто кривыми.

Кривая Жордана

Кривой Жордана называется образ непрерывного инъективного отображения окружности или отрезка в пространство. В случае окружности кривая называется замкнутой кривой Жордана, а в случае отрезка — жордановой дугой или простой дугой.

Следует отметить что кривая Жордана является довольно сложным объектом, например возможно построить плоскую кривую Жордана с ненулевой мерой Лебега.

Комментарий

Существует большой соблазн определить кривую как образ непрерывного отображения отрезка в пространство.

Однако возможно построить такое непрерывное отображение отрезка в плоскость, что его образ заполняет квадрат, например, кривая Пеано. Более того, согласно теореме Мазуркевича, компактное связанное и локально связанное топологическое пространство является непрерывным образом отрезка. Таким образом, не только квадрат, но и куб любого числа измерений и даже гильбертов кирпич являются непрерывными образами отрезка.

Вышеизложенное показывает, что кривая не может быть определена как непрерывный образ отрезка, если на отображение не наложить дополнительных ограничений.

Аналитические определения

В аналитической геометрии кривая на плоскости определяется как множество точек, координаты которых удовлетворяют уравнению F(x,y) = 0 . При этом на функцию F накладываются ограничения, которые гарантируют, что

• это уравнение имеет бесконечное множество несовпадающих решений и,
• это множество решений не заполняло «куска плоскости».

Алгебраические кривые

Важный класс кривых составляют те, для которых функция F(x,y) есть многочлен от двух переменных. В этом случае кривая, определяемая уравнением F(x,y) = 0 , называется алгебраической.

• Алгебраические кривые, задаваемые уравнением 1-й степени, суть прямые.
• Уравнение 2-й степени, имеющее бесконечное множество решений, определяет квадрики, то есть вырожденные и не вырожденные конические сечения.
• Примеры кривых, задаваемых уравнениями 3-ей степени: циссоида Диокла, Декартов лист.
• Примеры кривых 4-ой степени: лемниската Бернулли и овал Кассини.
• Пример кривой, определяемой уравнением чётной степени: (многофокусная) лемниската.

Алгебраические кривые, определяемые уравнениями высших степеней, рассматриваются в алгебраической геометрии. При этом бо́льшую стройность приобретает их теория, если рассмотрение ведется на комплексной проективной плоскости. В этом случае алгебраическая кривая определяется уравнением вида

где F — однородный многочлен трех переменных, являющихся проективными координатами точек.

Типы кривых

• Плоская кривая — кривая, все точки которой лежат в одной плоскости.
• Простая дуга
• Путь — непрерывное отображение отрезка [0,1] в топологическое пространство.
• Трансцендентная кривая

Типы точек на кривой

Обобщённые кривые

Более общее определение кривой для случая плоскости было дано Кантором в 1870-e годы:

Канторовой кривой называется компактное связное подмножество плоскости, такое что его дополнение всюду плотно.

Важный пример канторовой кривой доставляет ковёр Серпинского. Какова бы ни была канторова кривая L , она может быть вложена в ковёр Серпинского, то есть в ковре Серпинского содержится подмножество L‘ , гомеоморфное L . Таким образом ковёр Серпинского является универсальной плоской канторовой кривой.

В последствии это определение было обобщено Урысоном:

Кривой Урысона называется связное компактное топологическое пространство C топологической размерности 1.

Ковёр Серпинского удовлетворяет этому определению, так что всякая канторова кривая является также и кривой Урысона. Обратно, если плоский связный компакт является кривой Урысона, то он будет канторовой кривой.

См. также

Литература

• Бураго Д. Ю., Бураго Ю. Д., Иванов С. В. Курс метрической геометрии НИЦ РХД, Институт компьютерных исследований, Инст-т компьют. исслед., Ин-т комп.исслед., ИКИ, , ISBN 5-93972-300-4, 2004
• Математический энциклопедический словарь. М. «Советская энциклопедия», 1988 г.

Ссылки

Неплоские кривые Винтовая линия • Линия откоса • Локсодрома • Ортодромия • Губка Связанные понятия Определения кривой Аналитическая кривая • Кривая Жордана • Канторова кривая • Кривая Урысона Преобразованные кривые Эволюта • Эвольвента • Каустика