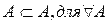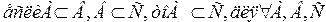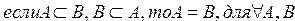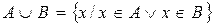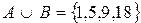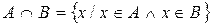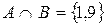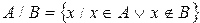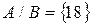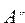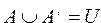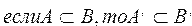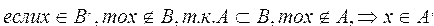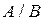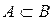О пустом множестве
Записано 13 декабря 1972 г .
Часто в математической литературе «легко» доказывается, что пустое множество
является подмножеством любого другого (пустого или непустого) множества.
Основой такого доказательства служат приводимые ниже определения
подмножества и пустого множества (курсив и полужирный шрифт везде мои):
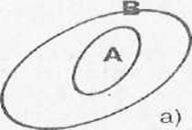
1. Множество А называется подмножеством множества В, если все элементы,
из которых состоит А, входят и в В. Это соотношение символически обозначается
так: А (или А L В; извините, но правильных знаков в Спецсим-ах я не нашёл)
2. Множество, не содержащее ни одного элемента, называется пустым
и обозначается символом Ǿ (или обычным нулём: 0).
Совершенно очевидно, что в первом определении речь идёт о двух непустых
множествах, поскольку в каждом предполагается наличие элементов, которые
и сравниваются между собой.
Теперь посмотрим, как же на основании определения подмножества, которое
ЯВНО предполагает НАЛИЧИЕ элементов как во множестве, так и в его подмножестве,
доказывается, что пустое множество, определение которого ЯВНО предполагает
ОТСУТСТВИЕ элементов в нём, является подмножеством любого (пустого или
«… Пустое множество есть подмножество любого множества. Чтобы установить это,
надо доказать, что если А есть произвольное множество, то каждый элемент Ǿ
(вот именно: КАЖДЫЙ элемент Ǿ, а в Ǿ ИХ НЕТ! – Н.М.) есть элемент подмножества А.
Поскольку Ǿ не имеет элементов, то условие выполняется автоматически».
(Какая-то казуистика! – Н.М.)
Итак, «доказали»: каждый элемент Ǿ есть элемент А! Ну и ну! Так, чего доброго,
можно доказать и противоположное: Ǿ не является подмножеством А,
поскольку Ǿ не содержит элементов! Или ещё интереснее: поскольку А не содержит
ни одного элемента из Ǿ. Каково! Попробуй, опровергни!
«… По определению любой субъект универсума не входит в пустое множество Ǿ .
Тем самым всякий элемент пустого множества содержится в любом множестве М.
А значит, любое множество М содержит пустое подмножество».
Голова моя явно слаба понять это. Ведь можно сказать и так:
По определению любой субъект универсума не входит в пустое множество Ǿ .
Тем самым ни какой элемент пустого множества не содержится ни в каком
множестве М. А значит, никакое множество М не может содержать в качестве
подмножества пустое множество».
Пожалуй, разум более приемлет второе утверждение, как более понятное; – «раз нет,
то и говорить нечего», чем утверждение – «хотя нет, но есть:» (не путать с «понятным»
определением – « хотя и нет, но можно говорить…»)
«… Заметим, между прочим, что из определения отношения А следует, что,
каково бы ни было подмножество А множества J
Таким образом, «доказательства» во всех рассмотренных случаях
аналогичны. Чувствуя неубедительность своих аргументов, некоторые авторы
приводят «косвенные» доказательства того, что Ǿ
«… Хотя такое рассуждение (смотрите выше – Н.М.) правильно, в нём имеется
нечто неудовлетворительное. Имеется и другое, косвенное доказательство,
которое может оказаться более удобным. Это может быть лишь в том случае,
если существует (да нету их там вообще. – Н.М.) некоторый элемент Ǿ ,
не являющийся множества А. Но это невозможно, так как Ǿ не имеет элементов.
Нетрудно провести аналогичное по форме «доказательство» противоположного
факта: Ǿ не принадлежит А. Действительно. Допустим, что Ǿ не принадлежит А
ложно (т.е. Ǿ – истинно). Это может быть лишь в том случае, если
множество А содержит все элементы множества Ǿ . Но это невозможно, так
как во множестве А , очевидно, нельзя найти и одного элемента, принадлежащего
пустому множеству, т.к. Ǿ не имеет элементов. . Значит, «Ǿ не принадлежит А»
не является ложным, т.е. Ǿ не принадлежит А ».
«… Свойство 4) (см. выше – Н.М.) может показаться несколько парадоксальным,
но если вдуматься (я очень пытался, но оказался слабоват – Н,М,), оно логически
строго соответствует точному смыслу определения знака
В самом деле, соотношение Ǿ нарушалось бы только в том случае,
если бы пустое множество Ǿ содержало элемент(да нету их там вообще. – Н.М.),
который не содержался бы в А, но так как пустое множество не содержит вовсе
элементов, то этого быть не может, каково бы ни было А».
А вот аналогичное по форме, но противоположное по результатам доказательство;
соотношение Ǿ не принадлежит А нарушалось бы только в том случае, если бы
множество А содержало бы все элементы … и т.д. и т.п. ( смотрите ранее
приведённое «контрдоказательство»).
Итак, любое доказательство утверждения Ǿ
На мой взгляд дать определение подмножества так, чтобы соотношение Ǿ
являлось его следствием, НЕЛЬЗЯ! Дело в том, что пустое множество
КАЧЕСТВЕННО отличается от непустого именно тем, что оно не содержит элементов.
Т. е. их вообще нелогично сравнивать!
Да, трудно доказать ЧТО-ТО, когда в разряд ЧЕГО-ТО зачисляется НИЧТО.
А поэтому удобное и необходимое для нас соотношение Ǿ нужно просто
ПОСТУЛИРОВАТЬ. Я так думаю.
«… Если, как это уже предполагалось выше, ввести в рассмотрение так
называемое пустое множество, т. е. множество, не содержащее ни одного
элемента, то пустое множество придётся (вот именно! – Н.М .) формально считать подмножеством любого другого множества (пустого или непустого)»
Некоторые авторы (см. например [5], стр. 14) фактически так и поступают.
Не исключено, однако, что здесь имеет место отказ от доказательства соотношения
Ǿ ввиду его «очевидности»
«… Если, как это уже предполагалось выше, ввести в рассмотрение так
называемое пустое множество, т. е. множество, не содержащее ни одного
элемента, то пустое множество придётся (вот именно! – Н.М .) формально считать подмножеством любого другого множества (пустого или непустого)»
Подредактировано 17.03.2013 9:26
Литература:
[1], Множества. Логика. Аксиоматические теории,Роберт Р. Стол: «Просвещение», М. 1968 г . (перевод с английского).
Р. Курант и Г. Робинс, «Просвещение», М. 1967 г . (перевод с английского).
[4], «Математика в школе» №3, 1967 г . «Просвещение», [5], Элементы теории функций и функционального анализаА. Н. Колмогоров, С. В. Фомин, «Наука», М. 1972 г .
Интересно сравнить
В некоторых формулировках теории множеств существование
пустого множества постулируется (см. аксиому пустого множества),
в других — доказывается.
Тема: «Около «науки»
Страницы : 23, 24, 40, 41, 77, 78, 79.
Источник статьи: http://cmex-x2007.narod.ru/PUSTOE.htm
Что такое пустое множество? Какие у него принципы? Как его доказать?
Пустое множество — это множество, в котором отсутствуют элементы. Пустное множество — это определение, его невозможно доказать, потому что доказывают только теоремы.
Можно сказать, что пустое множество в математике — это то же самое, что и ноль в арифметике. Оно также необходимо.
Пустое множество — множество в котором нет ни одного элемента. Вот и весь принцип. Пустое множество так же необходимо в математике, как и ноль в арифметике. А что значит доказать множество — загадка. Доказывать можно теоремы, а не определения.
Объясните теорему Гёделя о неполноте простым языком для нематематика пожалуйста. Постулаты, практическое значение, влияние на философию?
Во-первых их две. Но связанных друг с другом.
Во-вторых это сильные запретительные теоремы. На простом языке смыслов два:
Первый: если некая система математических аксиом включает в себя аксиомы арифметики, то к этой системе аксиом можно добавлять еще аксиомы, непротиворечащие уже существующим, и в рамках этой новой системы аксиом не будут существовать противоречивые утверждения.
Второй: Если аксиомы арифметики в системе аксиом не включены, то противоречивые утверждения в этой системе аксиом обязательно будут.
Это некая проблема для всех гуманитарных наук, которые хотели бы «математизироваться», но как включить арифметику в историю, социологию, психологию, искусствоведение, например? Где там в исторических процессах «ноль», «единица», «сложение», «умножение», «коммутативность», «транзитивность» — не ясно — значит любая построенная «историческая алгебра» будет компрометируема — возникнут противоречия, то есть одновременное выполнение утверждений «А» и «не А».
То есть «поверить алгеброй гармонию» оказывается заведомо, математически, невозможно — к счастью для гармонии — представьте, что кто-то придумал некую математику, в рамках которой Штраус в пи раз хуже Баха — уже не смешно. ))) Ссылаясь на теорему Гёделя, можно спокойно говорить, что это утверждение заведомо неверно, поскольку получено в рамках противоречивой теории.
Для естественных наук теоремы Гёделя не открыли ничего нового — с арифметикой эти науки дружат, и интуитивно всегда было понятно, что в физике, к примеру, можно навыдумывать бесконечно много разных законов — не все конечно получат экспериментальное подтверждение, но математических противоречий не возникнет.
Философы и психологи-социологи, теорему(ы) Гёделя, в основном, не любят :))))).
Источник статьи: http://yandex.ru/q/question/hw.math/chto_takoe_pustoe_mnozhestvo_kakie_u_nego_feba7a1b/
Множество и его элементы. подмножество. пустое множество.
Понятие множества – одно из основных понятий математики. Под множеством понимают совокупность объектов (предметов или понятий), которая рассматривается как единое целое. Например, можно говорить о множестве натуральных чисел, о множестве букв на данной странице, о множестве корней данного уравнения и т. п. Понятие множества принимается как исходное, первичное, т. е. несводимое к другим понятиям. Объекты, входящие в состав множества, называются его элементами. Обычно множества обозначаются большими печатными буквами английского алфавита, например, множество А; а его элементы маленькими прописными буквами, например, элемент а.
Запись 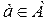
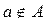
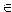
Определение 1. Два множества А и В называются равными и пишут А=В, если множества А и В содержат одни и те же элементы.
Например: <2, 4, 6>= <4, 2, 6>– равные множества.
Определение 2. Множество называется непустым, если содержит хотя бы один элемент.
Определение 3. Множество А является подмножеством множества В, если каждый элемент множества А принадлежит множеству В.
В этом случае пишут 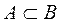
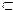
Например: <2, 4,>
Рассмотрим свойства отношения включения.
рефлексивно, т.е любое множество является подмножеством самому себе.
транзитивно, т. е. для любых множеств А, В и С, если множество А является подмножеством множества В и множество В является подмножеством множества С, то из этого следует, что множество А является подмножеством множества С.
антисимметрично, т. е. для любых множеств А и В следует, что, если множество А является подмножеством множества В и в то же время множество В является подмножеством множества А, то множества А и В равны.
Определение 4. Множество, не содержащее ни одного элемента, называется пустыммножеством.

Пустое множество является подмножеством любого множества.
Определение 5. Множество всех подмножеств множества A называется множеством-степенью и обозначается P(A).
В дальнейшем будем пользоваться следующим утверждением:
Утверждение 1. Число всех подмножеств конечного множества равно 2n.
Пример. Выделим все подмножества множества А =<2, 4, 6>.
Р(А)=<2, 4, 6>, <2, 4>, <4, 6>, <2, 6>, <2>, <4 >, <6>, 
Операции над множествами
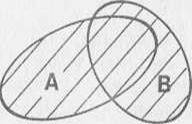
Объединением множеств А и В называется множество, состоящее из тех элементов, которые принадлежат одному из множеств А или В.
Для обозначения объединения множеств используют знак 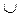
Пример. 

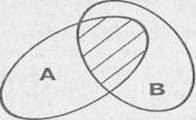
Пересечением множеств А и В называются такое множество, элементы которого принадлежат как множеству А, так и множеству В.
Для обозначения пересечения множеств используют знак 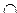
Пример. 

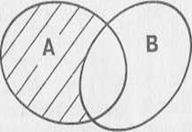
Разностью множеств А и В называется множество, элементы которого являются элементами множества А, не принадлежащие множеству В.
Для обозначения разности множеств используют знак /.
Пример. 

Перечислим основные свойства операций над множествами:
1) 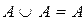
2) 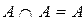
3) 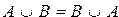
4) 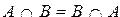
5) 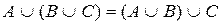
6) 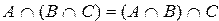
7) 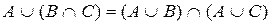
8) 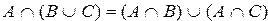
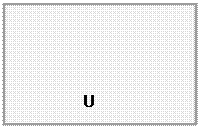
Универсальное множество. Дополнение множества.
Во многих приложениях теории множеств рассматриваются только такие множества, которые содержатся в некотором фиксированном множестве. Например, в геометрии мы имеем дело с множеством точек данного пространства, в арифметике – с множеством целых чисел. Такое фиксированное множество называют универсальным.Для его обозначения используют букву U.
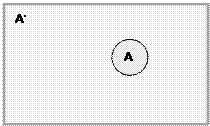
Определение 6. Множество U/А называется дополнением множества А и обозначается 

Дополнение U/ 

Справедливы следующие формулы:
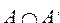
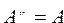
Теорема. Если множество А является подмножеством множества В, то дополнение множества А будет являться подмножеством дополнения множества В.
Пусть множество А является подмножеством множества В, 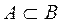
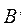

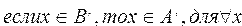
Действительно, если х принадлежит множеству 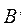

Теорема. Имеют место следующие тождества
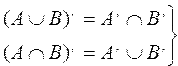
Приведем краткое доказательство первого утверждения.
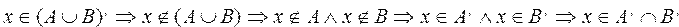
Для графического изображения множеств и их свойств используются так называемые диаграммы Эйлера-Венна.
Объединение множеств Пересечение множеств
Разность множеств Подмножество
Универсальное множество Дополнение
 |  |
Понятие множества. Элементы множества. Пустое множество. Принадлежность элементов.
Источник статьи: http://csaa.ru/mnozhestvo-i-ego-jelementy-podmnozhestvo-pustoe/