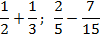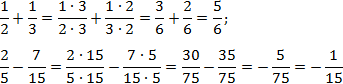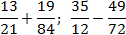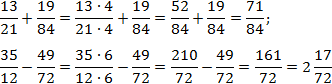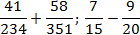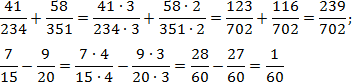Как пишется приведение к общему знаменателю

«Привидение» или «приведение»: как правильно пишется?

В русском языке часто случается, что изменение одной буквы придает слову иной смысл. Поскольку слова остаются близкими по звучанию, возникают затруднения, как правильно пишутся требуемые лексемы. Грамотное написание «привидение» или «приведение» из этого ряда. Чтобы не ошибиться в орфографии, надо понимать разницу между ними.

Как правильно написать: «привидение» и «приведение»?

Оба слова соответствуют грамматическим правилам русского языка и имеют право на существование.

«Привидение» сформировано от глагола «привидеться», «привиделось». Эти слова являются проверочными для правильного написания гласной в корне словоформы «привидение». Надо писать букву «и».

Существительное «приведение» восходит к глаголу «приводить», «привести». В этом слове в разных лексических формах чередуются звуки «е» и «о», так называемые беглые гласные.

Когда надо писать «привидение»

Если одна буква меняет смысл слова, необходимо представлять, о чем идет речь.

«Привидением» в традиционных воззрениях называют зрительное или какое-то другое появление в реальности духа умершего человека.

В доисторическом обществе люди поклонялись духам предков, там укоренился анимизм, подразумевавший наличие духов в реальной жизни. Они появлялись в виде «привидений».

Позже феномен «привидений» распространили на возникновение призраков самых разных существ, предметов, объектов. Звери, корабли (легенда о Летучем голландце), самолеты, военные отряды, города.

Во всех случаях, когда мы говорим о воплощении наяву чего-то, что не может существовать здесь и сейчас, мы произносим слово «привидение», проговаривая во втором слоге букву «и». У словоформы есть приставка «при». Ее написание необходимо запомнить либо уточнить в орфографическом словаре.

Слово имеет синонимы. Самый распространенный ̶ «призрак». Употребляют также «фантом», «мираж». Поэты любят использовать «фата-моргана».

Морфология лексемы «привидение»

Имя существительное среднего рода, нарицательное, может быть одушевленным или неодушевленным. В зависимости от контекста употребляется как разные члены предложения.

«Привидение» содержит все основные части слова:

• «при» ̶ приставка;
• «вид» ̶ корень;
• «ени» ̶ суффикс;
• «е» ̶ окончание.

Примеры использования в предложениях

1. Олег не сомневался, что ему явилось привидение.
2. Я шел по темному переулку, и мне, казалось, что сейчас встречу привидение.
3. После карантина из-за коронавируса Елена выглядела как привидение.

В каких случаях надо писать «приведение»

Как и в других случаях со словами прохожего звучания, чтобы не ошибиться в орфографии, надо понимать обстоятельства, когда используется данное слово. В нашем случае «приведение».

Это существительное берет начало от глагола «привести», «приводить». Оно употребляется в значении упорядочения, уточнения, преобразования. Может иметь также негативную коннотацию в смысле манипулирования.

Примеры

Астрономия. В этой науке «приведением» называют внесение небольших поправок в расчеты положения небесных объектов. Они зависят от времени и применяемого метода наблюдения.

Механика. В этой области под «приведением» понимают замену многих сил на результирующий вектор силы.

В логике есть понятие «приведение» к абсурду. Проводится анализ утверждения, и показывается его ошибочность, так как оно приводит к абсурду, противоречиям. Подобной техникой мастерски владел Сократ.

В математике схожая операция носит название «приведение» к нелепице. Кроме того, в царице наук термин «приведение» означает преобразование переменной из одного вида в другой.

В обыденной жизни в основном слово используется в смысле упорядочить: дела, архив, мысли, отношения с другими людьми. Также применяется в контексте задать норму, свести к общему знаменателю, стандарту.

Во всех случаях при написании слова «приведение» во втором слоге используется буква «е». Иное неверно.

В русском языке существует несколько синонимов этого словообразования: придание соответствующего вида, упорядочивание, преобразование, нормирование.

Морфология лексемы «приведение»

Имя существительное среднего рода, нарицательное, неодушевленное. Может служить разными членами предложения.

Разбивается на следующие части слова:

• «при» ̶ приставка;
• «вед» ̶ корень;
• «ени» ̶ суффикс;
• «е» ̶ окончание.

Образцы использования в предложениях

1. Приведение документа в соответствие с законодательством заняло два дня.
2. Отдохнув, я занялся приведением архива в порядок.
3. Для приведения квартиры в надлежащий вид потребуется ремонт.

Заключение

Для понимания, как правильно писать лексемы «привидение» и «приведение», необходимо понимать ситуацию, когда употребляется слово.

Близкие по звучанию, но имеющие разные значения слова требуют внимания к орфографии, предварительного анализа различий двух сходных словоформ. Пренебрежение к правописанию может исказить мысль, привести к неверному толкованию и даже поставить автора в комичное, нелепое положение. Во избежание этого целесообразно пользоваться толковыми и орфографическими словарями.

Источник статьи: http://znanieinfo.ru/orfografiya/prividenie-ili-privedenie.html

Приведение дробей к общему знаменателю

Изначально я хотел включить методы приведения к общему знаменателю в параграф «Сложение и вычитание дробей». Но информации оказалось так много, а важность ее столь велика (ведь общие знаменатели бывают не только у числовых дробей), что лучше изучить этот вопрос отдельно.

Итак, пусть у нас есть две дроби с разными знаменателями. А мы хотим сделать так, чтобы знаменатели стали одинаковыми. На помощь приходит основное свойство дроби, которое, напомню, звучит следующим образом:

Дробь не изменится, если ее числитель и знаменатель умножить на одно и то же число, отличное от нуля.

Таким образом, если правильно подобрать множители, знаменатели у дробей сравняются — этот процесс называется . А искомые числа, «выравнивающие» знаменатели, называются .

Для чего вообще надо приводить дроби к общему знаменателю? Вот лишь несколько причин:

1. Сложение и вычитание дробей с разными знаменателями. По-другому эту операцию никак не выполнить;
2. Сравнение дробей. Иногда приведение к общему знаменателю значительно упрощает эту задачу;
3. Решение задач на доли и проценты. Процентные соотношения являются, по сути, обыкновенными выражениями, которые содержат дроби.

Есть много способов найти числа, при умножении на которые знаменатели дробей станут равными. Мы рассмотрим лишь три из них — в порядке возрастания сложности и, в некотором смысле, эффективности.

Умножение «крест-накрест»

Самый простой и надежный способ, который гарантированно выравнивает знаменатели. Будем действовать «напролом»: умножаем первую дробь на знаменатель второй дроби, а вторую — на знаменатель первой. В результате знаменатели обеих дробей станут равными произведению исходных знаменателей. Взгляните:

Задача. Найдите значения выражений:

В качестве дополнительных множителей рассмотрим знаменатели соседних дробей. Получим:

Да, вот так все просто. Если вы только начинаете изучать дроби, лучше работайте именно этим методом — так вы застрахуете себя от множества ошибок и гарантированно получите результат.

Единственный недостаток данного метода — приходится много считать, ведь знаменатели умножаются «напролом», и в результате могут получиться очень большие числа. Такова расплата за надежность.

Метод общих делителей

Этот прием помогает намного сократить вычисления, но, к сожалению, применяется он достаточно редко. Метод заключается в следующем:

1. Прежде, чем действовать «напролом» (т.е. методом «крест-накрест»), взгляните на знаменатели. Возможно, один из них (тот, который больше), делится на другой.
2. Число, полученное в результате такого деления, будет дополнительным множителем для дроби с меньшим знаменателем.
3. При этом дробь с большим знаменателем вообще не надо ни на что умножать — в этом и заключается экономия. Заодно резко снижается вероятность ошибки.

Задача. Найдите значения выражений:

Заметим, что . Поскольку в обоих случаях один знаменатель делится без остатка на другой, применяем метод общих множителей. Имеем:

Заметим, что вторая дробь вообще нигде ни на что не умножалась. Фактически, мы сократили объем вычислений в два раза!

Кстати, дроби в этом примере я взял не случайно. Если интересно, попробуйте сосчитать их методом «крест-накрест». После сокращения ответы получатся такими же, но работы будет намного больше.

В этом и состоит сила метода общих делителей, но, повторюсь, применять его можно лишь в том случае, когда один из знаменателей делится на другой без остатка. Что бывает достаточно редко.

Метод наименьшего общего кратного

Когда мы приводим дроби к общему знаменателю, мы по сути пытаемся найти такое число, которое делится на каждый из знаменателей. Затем приводим к этому числу знаменатели обеих дробей.

Таких чисел очень много, и наименьшее из них совсем не обязательно будет равняться прямому произведению знаменателей исходных дробей, как это предполагается в методе «крест-накрест».

Например, для знаменателей 8 и 12 вполне подойдет число 24, поскольку . Это число намного меньше произведения .

Наименьшее число, которое делится на каждый из знаменателей, называется их (НОК).

Обозначение: наименьшее общее кратное чисел обозначается . Например, ; .

Если вам удастся найти такое число, итоговый объем вычислений будет минимальным. Посмотрите на примеры:

Задача. Найдите значения выражений:

Заметим, что . Множители 2 и 3 взаимно просты (не имеют общих делителей, кроме 1), а множитель 117 — общий.

Аналогично, . Множители 3 и 4 взаимно просты, а множитель 5 — общий.

Теперь приведем дроби к общим знаменателям:

Обратите внимание, насколько полезным оказалось разложение исходных знаменателей на множители:

1. Обнаружив одинаковые множители, мы сразу вышли на наименьшее общее кратное, что, вообще говоря, является нетривиальной задачей;
2. Из полученного разложения можно узнать, каких множителей «не хватает» каждой из дробей. Например, , следовательно, для первой дроби дополнительный множитель равен 3.

Чтобы оценить, насколько колоссальный выигрыш дает метод наименьшего общего кратного, попробуйте вычислить эти же примеры методом «крест-накрест». Разумеется, без калькулятора. Думаю, после этого комментарии будут излишними.

Не думайте, что таких сложных дробей в настоящих примерах не будет. Они встречаются постоянно, и приведенные выше задачи — не предел!

Единственная проблема — как найти этот самый НОК. Иногда все находится за несколько секунд, буквально «на глаз», но в целом это сложная вычислительная задача, требующая отдельного рассмотрения. Здесь мы не будем этого касаться.

Источник статьи: http://www.berdov.com/docs/fraction/common_denominator/

Приведение дробей к общему знаменателю

Общий знаменатель обыкновенных дробей

Если обыкновенные дроби имеют одинаковые знаменатели, то про эти дроби говорят, что они имеют общий знаменатель. Например, дроби

и

имеют общий знаменатель 7.

Общий знаменатель — это число, которое является знаменателем для двух и более обыкновенных дробей.

Дроби, имеющие разные знаменатели, можно привести к общему знаменателю.

Приведение дробей к общему знаменателю

Приведение дробей к общему знаменателю — это замена данных дробей, имеющих разные знаменатели, на равные им дроби, у которых одинаковые знаменатели.

Дроби можно привести либо просто к общему знаменателю, либо к наименьшему общему знаменателю.

Наименьший общий знаменатель — это наименьшее общее кратное знаменателей данных дробей. Чтобы привести дроби к наименьшему общему знаменателю нужно:

1. Выполнить сокращение дробей, если это возможно.
2. Найти наименьшее общее кратное знаменателей данных дробей. Именно НОК и станет их наименьшим общим знаменателем.
3. Разделить НОК на знаменатели данных дробей. Этим действием мы находим дополнительный множитель для каждой из данных дробей. Дополнительный множитель — это число, на которое надо умножить члены дроби, чтобы привести её к общему знаменателю.
4. Умножить числитель и знаменатель каждой дроби на дополнительный множитель.

Пример. Привести к общему знаменателю дроби и .

Находим НОК знаменателей данных дробей:

Находим дополнительные множители:

24 : 8 = 3 (для )

24 : 12 = 2 (для ).

Умножаем члены каждой дроби на свой дополнительный множитель:

Приведение к общему знаменателю можно записывать в более краткой форме, указывая дополнительный множитель рядом с числителем каждой дроби (сверху справа или сверху слева) и не записывая промежуточные вычисления:

К общему знаменателю можно привести и более простым способом, умножив члены первой дроби на знаменатель второй дроби, а члены второй дроби — на знаменатель первой.

Пример. Привести к общему знаменателю дроби и :

В качестве общего знаменателя дробей можно взять произведение их знаменателей.

Приведение дробей к общему знаменателю используется при сложении, вычитании и сравнении дробей, у которых разные знаменатели.

Калькулятор приведения к общему знаменателю

Данный калькулятор поможет вам привести обыкновенные дроби к наименьшему общему знаменателю. Просто введите две дроби и нажмите кнопку Привести .

Источник статьи: http://izamorfix.ru/matematika/arifmetika/obschiy_znam.html