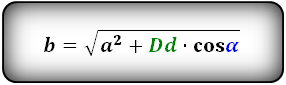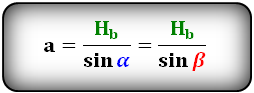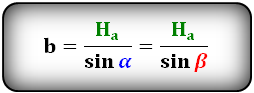Параллелограмм. Формулы, признаки и свойства параллелограмма
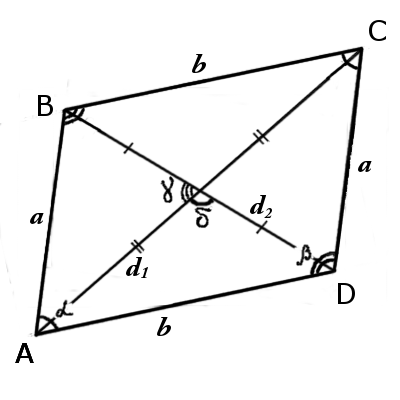 | 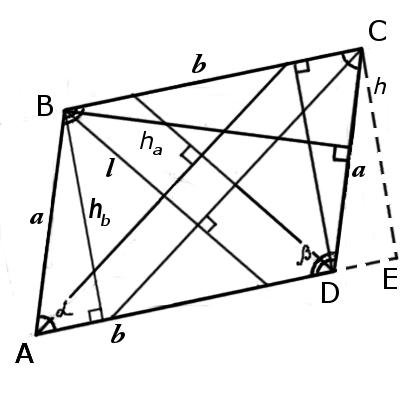 |
| Рис.1 | Рис.2 |
Признаки параллелограмма
AB||CD, AB = CD (или BC||AD, BC = AD)
∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = ∠DAB + ∠DAB = 180°
AC 2 + BD 2 = AB 2 + BC 2 + CD 2 + AD 2
Основные свойства параллелограмма
∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = ∠DAB + ∠DAB = 180°
8. Диагонали параллелограмма пересекаются и точкой пересечения делят друг друга пополам:
| AO = CO = | d 1 |
| 2 | |
| BO = DO = | d 2 |
| 2 |
Стороны параллелограмма
Формулы определения длин сторон параллелограмма:
1. Формула сторон параллелограмма через диагонали и угол между ними:
2. Формула сторон параллелограмма через диагонали и другую сторону:
| a = | √ 2 d 1 2 + 2 d 2 2 — 4 b 2 |
| 2 |
| b = | √ 2 d 1 2 + 2 d 2 2 — 4 a 2 |
| 2 |
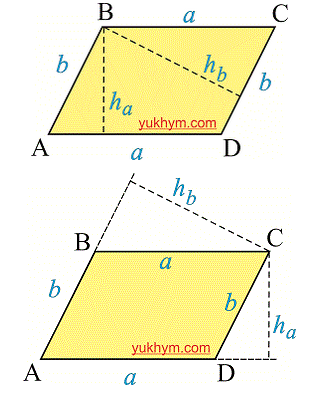
3. Формула сторон параллелограмма через высоту и синус угла:
| a = | h b |
| sin α |
| b = | h a |
| sin α |
Диагонали параллелограмма
Формулы определения длины диагонали параллелограмма:
d 1 = √ 2 a 2 + 2 b 2 — d 2 2
d 2 = √ 2 a 2 + 2 b 2 — d 1 2
4. Формула диагонали параллелограмма через площадь, известную диагональ и угол между диагоналями:
| d 1 = | 2S | = | 2S |
| d 2· sinγ | d 2· sinδ |
| d 2 = | 2S | = | 2S |
| d 1· sinγ | d 1· sinδ |
Периметр параллелограмма
Формулы определения длины периметра параллелограмма:
P = 2 a + √ 2 d 1 2 + 2 d 2 2 — 4 a 2
P = 2 b + √ 2 d 1 2 + 2 d 2 2 — 4 b 2
3. Формула периметра параллелограмма через одну сторону, высоту и синус угла:
| P = | 2( b + | h b | ) |
| sin α |
| P = | 2( a + | h a | ) |
| sin α |
Площадь параллелограмма
Формулы определения площади параллелограмма:
3. Формула площади параллелограмма через две диагонали и синус угла между ними:
| S = | 1 | d 1 d 2 sin γ |
| 2 |
| S = | 1 | d 1 d 2 sin δ |
| 2 |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Источник статьи: http://ru.onlinemschool.com/math/formula/parallelogram/
Периметр параллелограмма
Параллелограмм это геометрическая фигура имеющая четыре параллельные стороны, противоположных друг другу. В школьной программе все задания по решению параллелограмма, направлены на нахождение высоты, площади, диагонали и периметра. О них и пойдет речь.
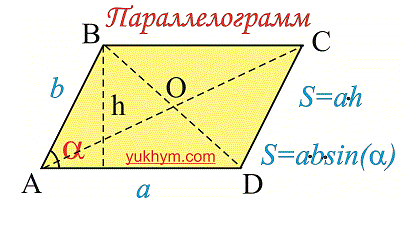
Параллелограмм обладает свойствами, такими как:
В параллелограмме и углы и стороны, которые противоположны между собой одинаковы: АВ = CD, BC =AD. Так же как углы АВС = ADC и ВАD = BCD.
Диагонали проведенные из углов параллелограмма в месте пересечения разделятся на две одинаковые части. АО = ОС, ОВ = OD.
Сумма двух углов, одной стороны всегда 180 градусов.
углы: А + В = 1800, В + С = 1800, С + D =1800, A + D = 1800 .
Любая диагональ разделяет параллелограмм на две одинаковые фигуры (треугольник) как по площади так и по размеру.
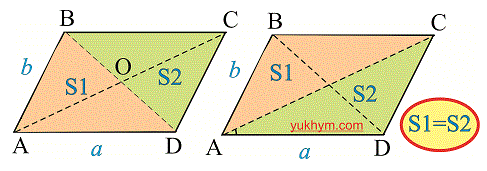
Зачастую встречается такое интересное свойство как, сума диагоналей в квадрате одинакова с суммой сторон в квадрате.
АС2 + BD2 = (AB2 + BC2). AC2 + BD2 = 2 * (AB2 + BC2)
У параллелограмма есть несколько основных признаков.
— Четырехугольная фигура с противоположными сторонами параллельными друг другу и есть параллелограмм.
— Четырехугольная фигура имеющая одинаковые противоположные стороны, есть параллелограмм.
— Четырехугольная фигура имеющая одинаковые параллельные и противоположные стороны, есть параллелограмм.
— Когда встречающиеся диагонали четырехугольной фигуры в месте пересечения разделяются на равные части. Данная фигура является параллелограммом.
— Четырехугольная фигура в которой противоположные углы одинаковы называется параллелограммом.
Периметр параллелограмма находится по формуле
что означает что периметр равняется двойной сумме сторон.
Биссектриса параллелограмма
Из школьной программы помню определение которое засело в памяти на всю жизнь — Биссектриса это крыса, что ходит по углам и делит угол пополам. Если же говорить научным языком, то:
Биссектрисы углов находящихся на одной стороне встречаются в точке пересечения под углом в 90 градусов.
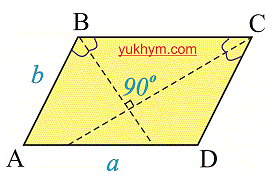
Так же они могут совпадать и быть параллельны друг другу.
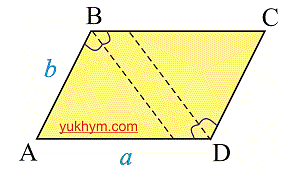
Так же в параллелограмме можно найти высоту, она обозначается в виде отрезка исходящего из угла к основанию, следовательно, от каждого угла их можно провести две.
Площадь параллелограмма это произведение стороны и высоты приведенную к ней. Находится по формуле.
S = a * ha = b * hb
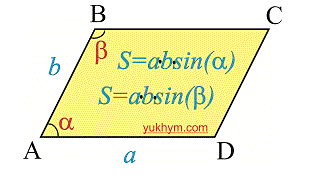
Есть еще один способ вычисления, но им не так часто пользуются в расчетах. Она звучит как площадь параллелограмма это произведение рядом лежащих сторон умноженный на синус угла находящегося между ними.
S = a * b * sin(?) = a * b * sin(?)
Все приведенные в данной статье формулы помогут Вам в решении различных задач по нахождению величин параллелограмма, это не сложно но очень интересно.
Заметка: если Вы находитесь в поиске персонала. Империя кадров поможет вам в этом вопросе. Просто перейдите по ссылке персонал временный (http://www.imperia.ru/client/temp_staff/) и узнайте подробнее.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Источник статьи: http://reshit.ru/perimetr-parallelogramma
Параллелограмм и его свойства
Сумма внутренних углов любого четырехугольника равна \(360^\circ\) .
Свойства параллелограмма:
\(\blacktriangleright\) Противоположные стороны попарно равны;
\(\blacktriangleright\) Диагонали точкой пересечения делятся пополам;
\(\blacktriangleright\) Противоположные углы попарно равны, а сумма соседних равна \(180^\circ\) .
Признаки параллелограмма.
Если для выпуклого четырехугольника выполнено одно из следующих условий, то это – параллелограмм:
\(\blacktriangleright\) если противоположные стороны попарно равны;
\(\blacktriangleright\) если две стороны равны и параллельны;
\(\blacktriangleright\) если диагонали точкой пересечения делятся пополам;
\(\blacktriangleright\) если противоположные углы попарно равны.
Площадь параллелограмма
Площадь параллелограмма равна произведению высоты на основание, к которому проведена эта высота.
Периметр параллелограмма равен \(100\) , его большая сторона равна \(32\) . Найдите меньшую сторону параллелограмма.
Так как у параллелограмма противоположные стороны равны, то его периметр равен удвоенной сумме его непараллельных сторон, тогда сумма большей и меньшей сторон равна \(100 : 2 = 50\) , значит, меньшая сторона параллелограмма равна \(50 — 32 = 18\) .
Периметр параллелограмма равен \(15\) . При этом одна сторона этого параллелограмма на \(5\) больше другой. Найдите меньшую сторону параллелограмма.
У параллелограмма противоположные стороны равны. Пусть \(BC = AB + 5\) , тогда периметр параллелограмма \(ABCD\) равен \(AB + BC + CD + AD = AB + AB + 5 + AB + AB + 5 = 4\cdot AB + 10 = 15\) , откуда находим \(AB = 1,25\) . Тогда меньшая сторона параллелограмма равна \(1,25\) .
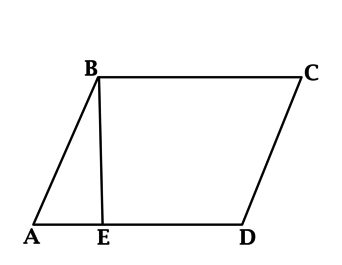
В параллелограмме \(ABCD\) : \(BE\) – высота, \(BE = ED = 5\) . Площадь параллелограмма \(ABCD\) равна 35. Найдите длину \(AE\) .
Площадь параллелограмма равна произведению основания на высоту, проведённую к этому основанию, тогда \(35 = BE \cdot AD = 5\cdot(5 + AE)\) , откуда находим \(AE = 2\) .
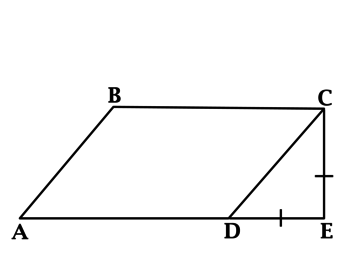
Из точки \(C\) параллелограмма \(ABCD\) опустили перпендикуляр на продолжение стороны \(AD\) за точку \(D\) . Этот перпендикуляр пересёк прямую \(AD\) в точке \(E\) , причём \(CE = DE\) . Найдите \(\angle B\) параллелограмма \(ABCD\) . Ответ дайте в градусах.
В равнобедренном треугольнике углы при основании равны, тогда \(\angle EDC = \angle DCE\) . Так как \(\angle DEC = 90^<\circ>\) , а сумма углов треугольника равна \(180^<\circ>\) , то \(\angle EDC = 45^<\circ>\) , тогда \(\angle ADC = 180^ <\circ>— 45^ <\circ>= 135^<\circ>\) . Так как в параллелограмме противоположные углы равны, то \(\angle B = \angle ADC = 135^<\circ>\) .
Диагональ \(BD\) параллелограмма \(ABCD\) перпендикулярна стороне \(DC\) и равна \(4\) . Найдите площадь параллелограмма \(ABCD\) , если \(AD=5\) .
По теореме Пифагора находим: \(AB^2=AD^2 — BD^2 = 25 — 16 = 9\) \(\Rightarrow\) \(AB = 3\) . \(S_
В параллелограмме \(ABCD\) : \(P_ <\triangle AOB>= 8\) , \(P_ <\triangle AOD>= 9\) , а сумма смежных сторон равна \(7\) . Найдите произведение этих сторон параллелограмма \(ABCD\) .
\(P_ <\triangle AOB>= AO + OB + AB\) , \(P_ <\triangle AOD>= AO + OD + AD\) , \(BO = OD\) \(\Rightarrow\) \(P_ <\triangle AOD>— P_ <\triangle AOB>= AD — AB = 1\) , но \(AD + AB = 7\) \(\Rightarrow\) \(AD = 4\) , \(AB = 3\) \(\Rightarrow\) \(AD\cdot AB = 12\) .
Стороны параллелограмма равны \(9\) и \(15\) . Высота, опущенная на первую сторону, равна \(10\) . Найдите высоту, опущенную на вторую сторону параллелограмма.
Площадь параллелограмма равна произведению высоты на сторону, к которой высота проведена. Следовательно, с одной стороны, площадь \(S=9\cdot 10\) , с другой стороны, \(S=15\cdot h\) , где \(h\) – высота, которую нужно найти.
Следовательно, \[9\cdot 10=15\cdot h\quad\Leftrightarrow\quad h=6\]
Задачи из раздела «Геометрия на плоскости» являются обязательной частью аттестационного экзамена у выпускников средней школы. Теме «Параллелограмм и его свойства» в ЕГЭ традиционно отводится сразу несколько заданий. Они могут требовать от школьника как краткого, так и развернутого ответа с построением чертежа. Поэтому если одним из ваших слабых мест являются именно задачи на вычисление площадей параллелограмма или его сторон и углов, то вам непременно стоит повторить или вновь разобраться в материале.
Сделать это легко и эффективно вам поможет образовательный портал «Школково». Наши опытные специалисты подготовили необходимый теоретический материал, изложив его таким образом, чтобы школьники с любым уровнем подготовки смогли восполнить пробелы в знаниях и легко решить задачи ЕГЭ на вычисление площадей, сторон, углов или свойства биссектрисы параллелограмма. Найти базовую информацию вы можете в разделе «Теоретическая справка».
Чтобы успешно решить задачи ЕГЭ по теме «Параллелограмм и его свойства», предлагаем попрактиковаться в выполнении соответствующих упражнений. Большая подборка заданий представлена в блоке «Каталог». Специалисты портала «Школково» регулярно дополняют и обновляют данный раздел.
Последовательно выполнять упражнения учащиеся из Москвы и других городов могут в режиме онлайн. При необходимости любое задание можно сохранить в разделе «Избранное» и в дальнейшем вернуться к нему, чтобы обсудить с преподавателем.
Источник статьи: http://shkolkovo.net/catalog/planimetriya_chast_i/parallelogramm_i_ego_svojstva
Как найти стороны параллелограмма
Свойства параллелограмма:
1. Противоположные стороны равны и параллельны
2. Противоположные углы равны
3. Точка пересечения диагоналей, делит их пополам
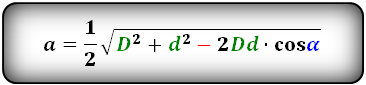
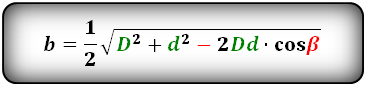
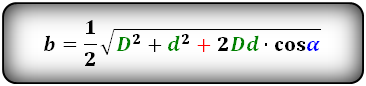
1. Формулы длины сторон через диагонали и угол между ними.
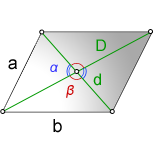
a , b — стороны параллелограмма
D — большая диагональ
d — меньшая диагональ
α , β — углы между диагоналями
Формулы сторон параллелограмма через диагонали и угол между ними (по теореме косинусов), ( a , b ):
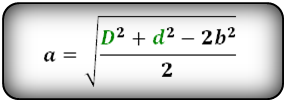
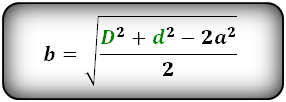
Формулы сторон параллелограмма через диагонали и сторону, ( a , b ):
Формулы сторон параллелограмма , ( a , b ):
2. Формулы длины сторон параллелограмма через высоту.
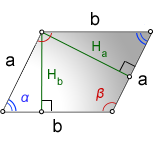
a , b — стороны параллелограмма
H b — высота на сторону b
H a — высота на сторону a
α , β — углы параллелограмма
Формулы сторон параллелограмма через высоту, ( a , b ):
3. Дополнительные, интересные формулы параллелограмма:
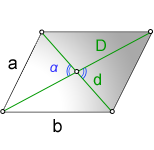
a , b — стороны параллелограмма
D — большая диагональ
d — меньшая диагональ
α — острый угол между диагоналями
Источник статьи: http://www-formula.ru/dlina-storon-parallelogramma