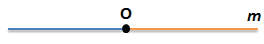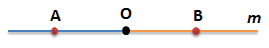Как пишется луч в геометрии

Точка, линия, прямая, луч, отрезок, ломанная | Математика (геометрия)

— это абстрактный объект, который не имеет измерительных характеристик: ни высоты, ни длины, ни радиуса. В рамках задачи важно только его местоположение

Точка обозначается цифрой или заглавной (большой) латинской буквой. Несколько точек — разными цифрами или разными буквами, чтобы их можно было различать

точка A, точка B, точка C

точка 1, точка 2, точка 3

— это множество точек. У неё измеряют только длину. Ширины и толщины она не имеет

Обозначается строчными (маленькими) латинскими буквами

линия a, линия b, линия c

Линия может быть

, если её начало и конец находятся в одной точке,
, если её начало и конец не соединены

замкнутые линии

разомкнутые линии

самопересекающиеся линии

линии без самопересечений

прямые линии

ломанные линии

кривые линии

— это линия которая не искривляется, не имеет ни начала, ни конца, её можно бесконечно продолжать в обе стороны

Даже когда виден небольшой участок прямой, предполагается, что она бесконечно продолжается в обе стороны

Обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами — точками, лежащими на прямой

прямая линия a

прямая линия AB

Прямые могут быть

, если имеют общую точку. Две прямые могут пересекаться только в одной точке.
- , если пересекаются под прямым углом (90°).
, если не пересекаются, не имеют общей точки.

параллельные линии

пересекающиеся линии

перпендикулярные линии

— это часть прямой, которая имеет начало, но не имеет конца, её можно бесконечно продолжать только в одну сторону

У луча света на картинке начальной точкой является солнце

солнышко

Точка разделяет прямую на две части — два луча

Луч обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами, где первая — это точка, с которой начинается луч, а вторая — точка, лежащая на луче

луч a

луч AB

Лучи совпадают, если

расположены на одной и той же прямой,
начинаются в одной точке,
направлены в одну сторону

лучи AB и AC совпадают

лучи CB и CA совпадают

— это часть прямой, которая ограничена двумя точками, то есть она имеет и начало и конец, а значит можно измерить её длину. — это расстояние между его начальной и конечной точками

Через одну точку можно провести любое число линий, в том числе прямых

Через две точки — неограниченное количество кривых, но только одну прямую

кривые линии, проходящие через две точки

прямая линия AB

От прямой «отрезали» кусочек и остался отрезок. Из примера выше видно, что его длина — наикратчайшее расстояние между двумя точками.

Отрезок обозначается двумя заглавными(большими) латинскими буквами, где первая — это точка, с которой начинается отрезок, а вторая — точка, которой заканчивается отрезок

отрезок AB

— это линия, состоящая из последовательно соединённых отрезков не под углом 180°

Длинный отрезок «поломали» на несколько коротких

(похожи на звенья цепи) — это отрезки, из которых состоит ломанная. — это звенья, у которых конец одного звена является началом другого. Смежные звенья не должны лежать на одной прямой.

(похожи на вершины гор) — это точка, с которой начинается ломанная, точки, в которых соединяются отрезки, образующие ломаную, точка, которой заканчивается ломанная.

Обозначается ломанная перечислением всех её вершин.

ломанная линия ABCDE

вершина ломанной A, вершина ломанной B, вершина ломанной C, вершина ломанной D, вершина ломанной E

звено ломанной AB, звено ломанной BC, звено ломанной CD, звено ломанной DE

звено AB и звено BC являются смежными

звено BC и звено CD являются смежными

звено CD и звено DE являются смежными

— это сумма длин её звеньев: ABCDE = AB + BC + CD + DE = 64 + 62 + 127 + 52 = 305

— это замкнутая ломанная линия

(помогут запомнить выражения: «пойти на все четыре стороны», «бежать в сторону дома», «с какой стороны стола сядешь?») — это звенья ломанной. — это смежные звенья ломанной.

— это вершины ломанной. — это точки концов одной стороны многоугольника.

Обозначается многоугольник перечислением всех его вершин.

Источник статьи: http://shpargalkablog.ru/2015/11/point-line-straight-ray-segment.html

Как пишется луч в геометрии

Луч — это часть прямой линии, расположенная по одну сторону от любой точки, лежащей на этой прямой. Луч также называется полупрямой.

Любой луч имеет начало и направление. Начало луча, начальная точка или вершина луча — это точка, из которой исходит луч. Таким образом, у луча есть начало, но нет конца.

Рассмотрим три луча с общим началом:

Все 3 луча имеют общую начальную точку O, но разные направления. Про каждый из них можно сказать: луч исходит из точки O или луч исходящий из точки O .

Дополнительные лучи

Любая точка, лежащая на прямой линии, делит эту прямую на две полупрямые, то есть на две части. Каждая из этих частей будет называться дополнительным лучом относительно второго луча:

Дополнительные лучи — это лучи, имеющие общее начало, противоположные направления и лежащие на одной прямой. Также можно сказать, что дополнительными называются лучи, дополняющие друг друга до прямой линии.

Обозначение лучей

Луч обозначают одной строчной латинской буквой:

Также луч можно обозначить двумя точками, лежащими на нём:

При обозначении луча двумя точками, на первом месте ставится буква, обозначающая начало луча, а на втором — буква, обозначающая какую-либо другую его точку: луч BC.

Посмотрим на следующий пример: