Как найти периметр квадрата
Основные определения
Квадратом принято называть правильный четырёхугольник, у которого равны все углы и стороны. Это частный случай прямоугольника, из-за чего можно заметить схожесть некоторых алгоритмов.
Периметр — это длина всех сторон многоугольника. Общепринятое обозначение — заглавная латинская буква P. Под «P» удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах по ходу решения.
Если параметры переданы в разных единицах длины, мы не сможем узнать какая площадь фигуры получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.
В чем измеряется периметр:
- квадратный миллиметр (мм 2 );
- квадратный сантиметр (см 2 );
- квадратный дециметр (дм 2 );
- квадратный метр (м 2 );
- квадратный километр (км 2 );
- гектар (га).
Формула нахождения периметра квадрата
Как находится периметр квадрата, всегда зависит от исходных данных. Рассмотрим две формулы, которые проходят 2 и 3 класс.
Если известна длина стороны
P = a + a + a + a, где a — сторона.
Так как все стороны фигуры равны, можно использовать формулу в таком виде: P = 4 * a
Если известна длина диагонали
P = d * 2 * √2, где d — диагональ.
Диагональ — это отрезок, который соединяет противоположные стороны фигуры.
Математика, как и любой другой предмет не сразу дается легко. Сложности могут возникать из-за неумения быстро делать простые арифметические действия — именно поэтому полезно практиковаться в решении примеров, как можно чаще. Давайте сделаем это прямо сейчас!
Решение задач
1. Найти периметр квадрата, диагональ которого равняется √4 см.
- Воспользуемся формулой P = d * 2 * √2;
- P = √4 * 2 * √2;
2. Найти периметр квадрата со стороной 97 мм. Записать ответ в сантиметрах
- Воспользуемся формулой P = 4 * a;
- P = 4 * 97
3. Периметр квадрата 48 см. Чему равна его сторона?
- Воспользуемся формулой P = 4 * a;
- Значит a = P : 4;
- a = 48 : 4;
4. Периметр квадрата 20 см. Как найти его площадь?
- Воспользуемся формулой P = 4 * a;
- Тогда a = P : 4;
- a = 20 : 4 = 5 см;
- Воспользуемся формулой S = a * a;
- Значит S = 5 * 5;
Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики в детскую школу Skysmart. Вместо скучных учебников ученики проходят интерактивные задания с автоматической проверкой, рисуют вместе с учителем на онлайн-доске и задают вопросы, которые бывает неловко спросить перед всем классом.
Источник статьи: http://skysmart.ru/articles/mathematic/perimetr-kvadrata
Периметр, формулы нахождения периметра
Периметр фигуры это длина всех ее сторон. Не все фигуры имеют периметр, например, шар не имеет периметра. Стандартное обозначение периметра в математике — буква P
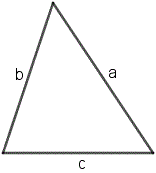
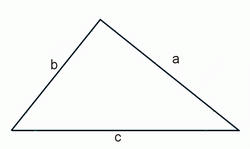
Периметр треугольника
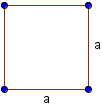
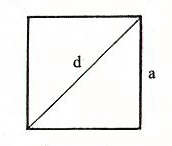
Периметр квадрата
Пусть длина стороны квадрата равна a . Квадрат имеет четыре равных стороны, поэтому периметр квадрата есть P = a + a + a +a или:
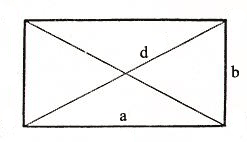
Периметр прямоугольника
Пусть длины сторон прямоугольника равны a и b .
Длина всех его сторон есть P = a + b + a + b или:
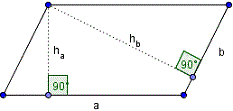
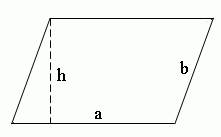
Периметр параллелограмма
Пусть длины сторон параллелограмма равны a и b
Длина всех его сторон есть P = a + b + a + b , поэтому периметр параллелограмма есть:
Как видно, периметр параллелограмма равен периметру прямоугольника.
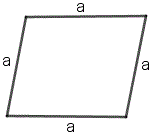
Периметр ромба
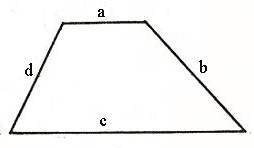
Периметр равнобедренной трапеции
Пускай длины параллельных сторон трапеции a и b , а длины двух других сторон равна c (Как известно, равнобедренная трапеция имеет две равные стороны).
Периметр равностороннего треугольника
Как известно, равносторонний треугольник имеет 3 равные стороны. Если длина стороны равна a , тогда формула нахождения периметра есть P = a + a + a
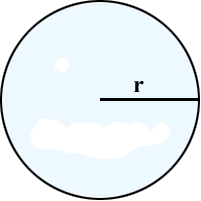
Длина окружности(периметр круга)
Обозначим длину окружности буквой l .
$l = d \cdot \pi = 2\cdot r \cdot \pi$
Где:
$\pi = 3,14$
r радиус круга (окружности)
d диаметр круга.
Правильный многоугольник
n число ребер(вершин).
$\pi = 3,14159265359$
Источник статьи: http://www.math10.com/ru/geometria/perimetr.html
Формула периметра.
Формула периметра определяет периметр фигуры, который является общей длиной границы фигуры, располагающейся в основном на плоскости.
Периметр имеет такую же размерность, что и длина. Бывает, что периметром называют границу геометрической фигуры. В большинстве случаев этот термин относится к треугольнику и многоугольникам и тогда это является суммой длин всех сторон фигуры. Таким образом, периметр — это сумма длин сторон какой-либо геометрической фигуры.
Полупериметр — половина периметра. Используется чаще всего только при работе с треугольниками.
| Геометрическая фигура | Формула | Чертеж |
|---|---|---|


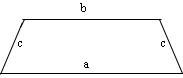
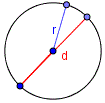
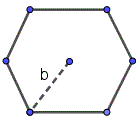












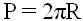
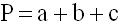
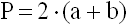
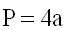
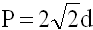
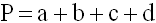

























 ,
,  ,
,  ,
,  ,
,  .
.  .
.  .
. ,
,  ,
,  .
. ,
,  ,
,  ,
,  ,
,  .
.