Как пишется деление в компьютере

Блог молодого админа

Увлекательный блог увлеченного айтишника

Знак деления на клавиатуре компьютера или ноутбука: как поставить?

Если вы печатаете с помощью клавиатуры своего компьютера или ноутбука математические примеры, то можете все символы набрать на самой клавиатуре. Не верите? В этой статье мы покажем пример со знаком деления. Способов будет несколько. Какой из них использовать, решать вам. Начнем с наиболее простого.

Двоеточие

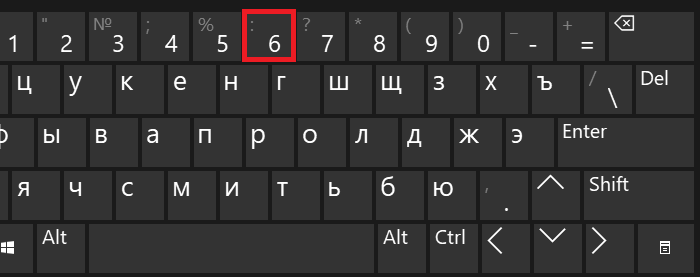
Надо отметить, что знаком деления могут выступать различные символы. Один из них — это двоеточие, находится он на той же клавише, что и цифра 6.

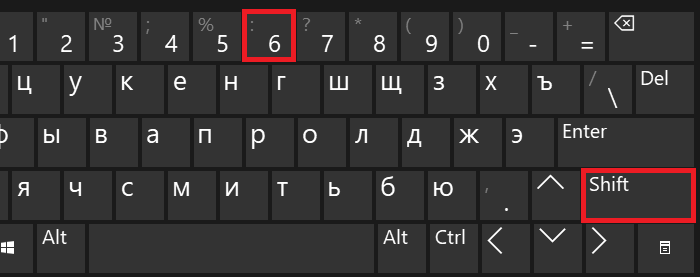
Чтобы поставить этот знак, нужно нажать на Shift и, удерживая клавишу, нажать на клавишу 6, после чего отпустить Shift.

Если вы вдруг увидели другой символ, это говорит о том, что у вас используется англоязычная раскладка. Переключите ее на русскоязычную, нажав на клавиши Shift+Ctrl:

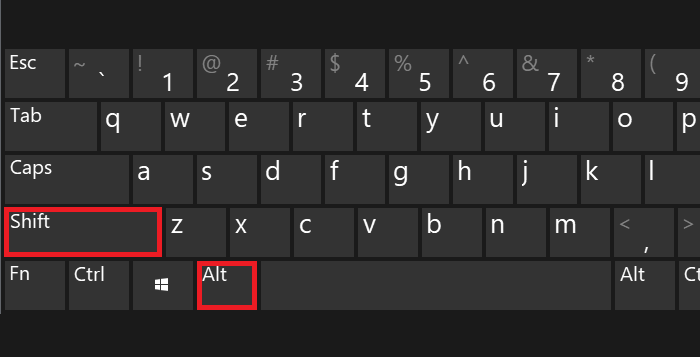
Можете также воспользоваться Alt-кодом. Для этого зажмите Alt и, удерживая его, наберите цифры 58, после чего отпустите Alt.

Если все сделано верно, вы увидите двоеточие.

Если не получилось с правым Alt, используйте левый.

Косая черта

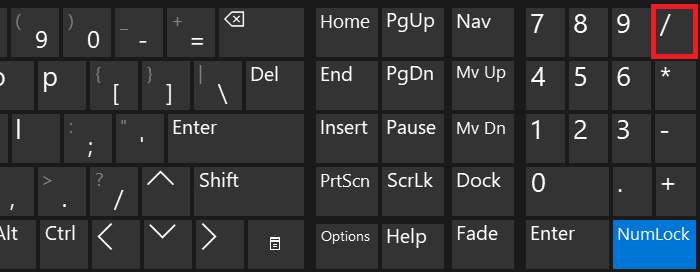
В качестве знака деления может выступать косая черта. Она находится рядом с цифровой клавиатурой.

Просто нажмите на нее один раз.

Раскладка клавиатуры роли не играет.

Alt-код для косой черты — 47:

Символ умножения из таблицы символов

Можете использовать таблицу символов Windows, чтобы указать обелюс (знак деления), который обычно встречается на калькуляторах.

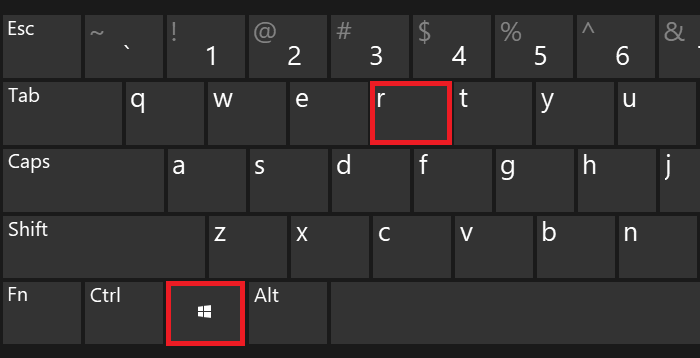
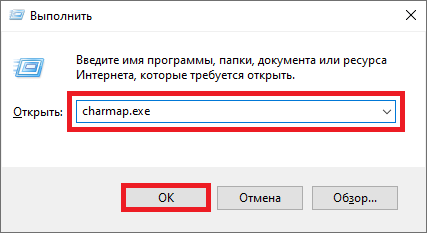
Затем в окно «Выполнить» введите команду charmap.exe и кликните ОК.

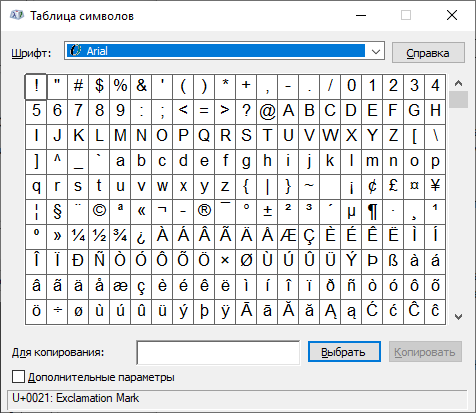
Если все сделали верно, увидите таблицу символов Windows.

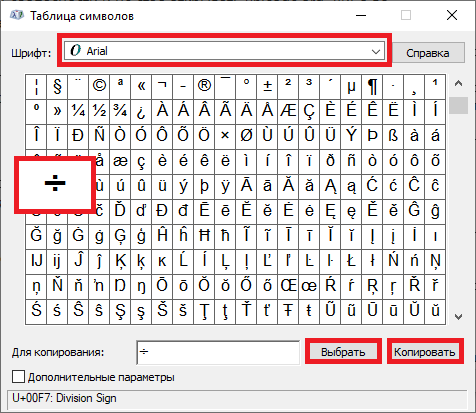
Выбираете шрифт Arial, находите символ деления, кликаете по нему, после чего кликаете по кнопкам «Выбрать» и «Копировать».

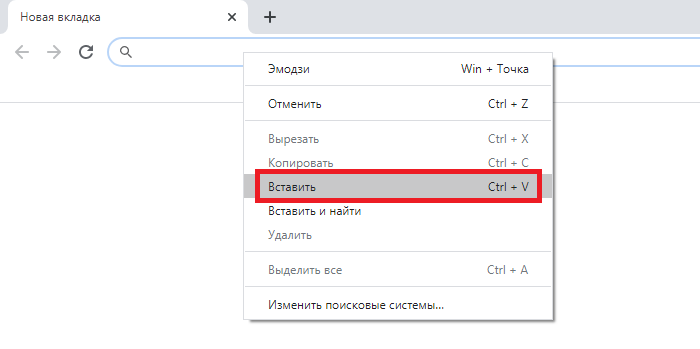
Можно использовать и Alt-коды.

В данном случае нужно набрать цифры 0247 на цифровой клавиатуре (англоязычная раскладка).

Источник статьи: http://fulltienich.com/znak-deleniya-na-klaviature-kompyutera-ili-noutbuka-windows/

Как сделать деление в столбик в ворде?

Нужно начать с того, что в программе ворд нет специального раздела, который мог бы позволить нарисовать деление в столбик. Поэтому в таких случаях, нужно проявлять творческую составляющую и решать иными путями данную задачу.

Таким образом, вариантов решения данной задачи множество, а я вам предлагаю на рассмотрение, на мой взгляд, один из простых. Перед нами стоит задача, разделить число 102 на 10 в столбик.

Первое, что я сделал, нашел онлайн калькулятор, искал его просто через строку поиска Яндекса, который мне решил поставленную задачу в своем сервисе, вот как выглядит ответ на одном из таких сайтов.

Следующим шагом, я сделал принскрин данного экрана, создал на компьютере «Точечный рисунок», через стандартное меню, как представлено ниже.

Открыл созданный файл программой Paint, которая стоит на всех виндусах по умолчанию, вот как она выглядит.

Программа Paint довольно простая и интуитивно понятная, от всего экрана я оставил вот такой маленький рисунок с формулой деления.

Открываю новый документ программы ворд, пишу небольшой текст: «Рассмотрим, как разделить число 102 на столбик:», после на верхней панели настроек заходим во вкладку «Вставка», где находим раздел «Иллюстрации» и нажимаем на иконку «Рисунок», находим наш рисунок и вставляем.

В итоге мы сделали в программе ворд деление в столбик.

Источник статьи: http://portalonline.ru/kompyutery-i-programmy/1839-kak-sdelat-delenie-v-stolbik-v-vorde.html

Как называется знак решётки? &, #, ÷, *

«Знак решётки», «деление», «вместо and», «звёздочка» , «буква R», «вопрос наоборот» — как правильно называются символы?

ДЕЛЕНИЕ — «ОБЕЛЮС»

От латинского obelus — от греческого ὀβελός. В этих словах тот же корень, что и в слове обелиск.

Именно так — обелюс — называется знак деления. Он напоминает объединение знаков минуса и двоеточия. Был введён древнегреческим филологом, александрийским библиотекарем Зенодотом Эфесским для обозначения сомнительности. Символ мог выглядеть либо как обычная горизонтальная черта, либо как та же черта, но с добавлением точек по одной сверху и снизу. Ставился на полях напротив тех частей текста, которые вызывали сомнения в ходе проверки поступавших в библиотеку рукописей.

В 1659 году немецкий математик Йоханн Ран в своей работе впервые применил обелюс для обозначения деления. Некоторые авторы использовали этот символ как знак вычитания, что стало нормой в некоторых странах Европы — например в Норвегии и Дании. В Польше обелюс использовался для обозначения диапазонов, например, запись 3÷7 означала «от трёх до семи».

РЕШЁТКА — ОКТОТОРП

От латинского octothorpe — восемь концов

Другие названия знака решётки — хеш, решётка, знак номера, диез или шарп (из-за внешнего сходства этих двух символов), знак фунта ( # часто используют в случаях, когда невозможно ввести символ фунта).

В 60-х годах XX века американские инженеры в области телефонии пытались придумать специальное название для этого символа, такие как октоторп, октаторп и октатерп. Однако ни одно из них так и не получило серьёзного распространения: все употребляли устоявшиеся формы hash sign (хеш-знак) или number sign (знак номера, который часто употребляют в английском языке).

Данный символ не был распространён в русской типографике вплоть до конца XX века. Неспециализированное, бытовое распространение знак получил с распространением цифрового набора номеров в телефонах. В языке за ним закрепился термин «знак решётки».

Источник статьи: http://zen.yandex.ru/media/tolk_slov/kak-nazyvaetsia-znak-reshetki——5aa95947610493d45934e7c0

Как написать дробь на клавиатуре: все способы

Если вы заняты написанием курсовой работы или документа с расчетной частью, вам может потребоваться графический символ, который отсутствует на клавиатуре. Это может быть значок иностранной валюты, символ функции или же математическая дробь. Рассмотрим последний случай. Существует несколько способов написания дроби на клавиатуре.

Вид №1: вертикальная дробь

Предположим, вы хотите изобразить дробь с горизонтальной чертой, которая называется винкулум. Пожалуй, это наиболее привычный для многих из нас вариант, ведь именно так учат записывать дроби школьные учителя математики, и именно это выражение встречается во многих технических, научных и образовательных текстах. В случае «многоэтажных» дробей вам нужно прибегнуть к безграничным возможностям Word.

Способ 1.

1. Установите курсор в том месте, куда необходимо вставить дробь;
2. Нажмите вкладку «Вставка»;
3. Найдите справа вкладку «Формула» и нажмите на нее;
4. В появившемся конструкторе найдите графу «Дробь» и выберите подходящий для вас вариант написания дроби: вертикальная простая или маленькая, которая пригодится для изображения смешанного числа, состоящего из целой и дробной части;
5. В указанном месте появится пустая формула. Вставьте необходимые цифры в пустых окошках дроби. Готово!

Способ 2.

1. Установите курсор в том месте, куда необходимо вставить дробь;
2. Нажмите вкладку «Вставка»;
3. Найдите справа вкладку «Объект» и нажмите на нее;
4. Выберите строку «Microsoft Equation 3.0» и нажмите ОК;
5. В появившейся поле с разнообразными символами выберите «Шаблоны дробей и радикалов» и нажмите на символ дробей;
6. Вставьте необходимые цифры в пустых окошках формулы.

Стоит учесть, что написание дробей в вертикальном виде отображается далеко не везде. Например, если вы скопируете вертикальную дробь из Word в чат социальных сетей или диалоговое окно Skype, то она отобразится в горизонтальном виде.

Вид №2: солидус

Вариант, часто встречающийся в научных работах, статьях и учебниках, — это дроби с наклонной чертой, которая в математическом мире называется «солидус». Эта дробная черта наклонена вправо приблизительно на 45°, а между цифрами существует специальный интервал (кернинг). Не путайте солидус с обычной косой чертой – они выглядят по-разному!

Изобразить дробь в таком виде можно при помощи Word. Используйте принцип действий, указанный в пункте «Вид №1», только во вкладке «Дробь» выберите вариант «диагональная простая дробь».

Ввести дробь в таком виде можно также через «Microsoft Equation 3.0».

Вид №3: горизонтальная дробь

Более привычный для нас вариант, который часто встречается в публицистических и научно-популярных статьях – это горизонтальная дробь.

Горизонтальную дробь можно ввести четырьмя способами:

• Вставка->Формула->Дробь->Горизонтальная простая дробь;
• Вставка->Символ->Числовые формы;В данном случае удобно осуществлять повторный ввод дробей — с помощью панели «Ранее использовавшиеся символы». Если вышеперечисленные дроби используется часто, можно настроить комбинации «горячих клавиш» или параметры автозамены.
• Вставка->Объект-> Microsoft Equation 3.0->Шаблоны дробей и радикалов.
• слэш

Самый простой и быстрый способ изобразить дроби, не прибегая к вставкам – использовать «слэш» (или косую черту, наклоненную вправо) на клавиатуре. Именно так поступает большинство пользователей Интернета, которые не желают тратить время на поиск нужных символов. Конечно же, для тех, кто занят написанием серьезных научных работ, лучше выбрать специальные изображения дробей.

Слэш располагается на клавиатуре в следующих местах:

• Рядом с правой кнопкой Shift на английской раскладке;
• В цифровом блоке;
• Над и слева от Enter (необходимо нажимать одновременно с Shift).

Вы также можете набрать слэш следующим образом:

1. Включите кнопку NumLock;
2. Зажмите Alt и наберите на цифровой клавиатуре 4 и затем 7;
3. Отпустите Alt.

Чтобы дробь, записанная через слэш, смотрелась естественнее, можно использовать следующую последовательность:

1. Выделить числитель дроби->Шрифт->Видоизменение->Надстрочный (ставим галочку) ->ОК;
2. Выделить знаменатель дроби->Шрифт->Видоизменение->Подстрочный (ставим галочку) -> ОК.

Теперь вы знаете, как написать дробь на клавиатуре. Как видите, это можно сделать самыми разными способами, и каждый из них достаточно прост. Желаем вам успехов в дальнейшем освоении компьютерной грамоты!

Источник статьи: http://lifeo.ru/kak-napisat-drob-na-klaviature/

Как пишется деление в компьютере

В большинстве компьютеров операция вычитания не используется. Вместо нее производится сложение обратных или дополнительных кодов уменьшаемого и вычитаемого. Это позволяет существенно упростить конструкцию АЛУ.

Сложение обратных кодов. Здесь при сложении чисел А и В имеют место четыре основных и два особых случая:

1. А и В положительные. При суммировании складываются все разряды, включая разряд знака. Так как знаковые разряды положительных слагаемых равны нулю, разряд знака суммы тоже равен нулю. Например:

Получен правильный результат.

2. А положительное, B отрицательное и по абсолютной величине больше, чем А. Например:

Получен правильный результат в обратном коде. При переводе в прямой код биты цифровой части результата инвертируются: 1 0000111 = –7 10 .

3. А положительное, B отрицательное и по абсолютной величине меньше, чем А. Например:

Компьютер исправляет полученный первоначально неправильный результат (6 вместо 7) переносом единицы из знакового разряда в младший разряд суммы.

4. А и В отрицательные. Например:

Полученный первоначально неправильный результат (обратный код числа –11 10 вместо обратного кода числа –10 10 ) компьютер исправляет переносом единицы из знакового разряда в младший разряд суммы. При переводе результата в прямой код биты цифровой части числа инвертируются: 1 0001010 = –10 10 .

При сложении может возникнуть ситуация, когда старшие разряды результата операции не помещаются в отведенной для него области памяти. Такая ситуация называется переполнением разрядной сетки формата числа. Для обнаружения переполнения и оповещения о возникшей ошибке в компьютере используются специальные средства. Ниже приведены два возможных случая переполнения.

5. А и В положительные, сумма А+В больше, либо равна 2 n–1 , где n — количество разрядов формата чисел (для однобайтового формата n=8, 2 n–1 = 27 = 128). Например:

Семи разрядов цифровой части числового формата недостаточно для размещения восьмиразрядной суммы (162 10 = 10100010 2 ), поэтому старший разряд суммы оказывается в знаковом разряде. Это вызывает несовпадение знака суммы и знаков слагаемых , что является свидетельством переполнения разрядной сетки .

6. А и В отрицательные, сумма абсолютных величин А и В больше, либо равна 2 n–1 . Например:

Здесь знак суммы тоже не совпадает со знаками слагаемых , что свидетельствует о переполнении разрядной сетки .

Сложение дополнительных кодов. Здесь также имеют место рассмотренные выше шесть случаев:

1. А и В положительные. Здесь нет отличий от случая 1, рассмотренного для обратного кода.

2. А положительное, B отрицательное и по абсолютной величине больше, чем А. Например:

Получен правильный результат в дополнительном коде. При переводе в прямой код биты цифровой части результата инвертируются и к младшему разряду прибавляется единица: 1 0000110 + 1 = 1 0000111 = –7 10 .

3. А положительное, B отрицательное и по абсолютной величине меньше, чем А. Например:

Получен правильный результат. Единицу переноса из знакового разряда компьютер отбрасывает.

4. А и В отрицательные. Например:

Получен правильный результат в дополнительном коде. Единицу переноса из знакового разряда компьютер отбрасывает.

Случаи переполнения для дополнительных кодов рассматриваются по аналогии со случаями 5 и 6 для обратных кодов.

Сравнение рассмотренных форм кодирования целых чисел со знаком показывает:

• на преобразование отрицательного числа в обратный код компьютер затрачивает меньше времени, чем на преобразование в дополнительный код, так как последнее состоит из двух шагов — образования обратного кода и прибавления единицы к его младшему разряду;
• время выполнения сложения для дополнительных кодов чисел меньше, чем для их обратных кодов, потому что в таком сложении нет переноса единицы из знакового разряда в младший разряд результата.

Умножение и деление

Во многих компьютерах умножение производится как последовательность сложений и сдвигов. Для этого в АЛУ имеется регистр , называемый накапливающим сумматором , который до начала выполнения операции содержит число ноль . В процессе выполнения операции в нем поочередно размещаются множимое и результаты промежуточных сложений , а по завершении операции — окончательный результат .

Другой регистр АЛУ, участвующий в выполнении этой операции, вначале содержит множитель . Затем по мере выполнения сложений содержащееся в нем число уменьшается , пока не достигнет нулевого значения.

Для иллюстрации умножим 110011 2 на 101101 2 .

Деление для компьютера является трудной операцией. Обычно оно реализуется путем многократного прибавления к делимому дополнительного кода делителя.

Источник статьи: http://mif.vspu.ru/books/informaticsshau/theory/chapter4/1_4_12.html