Как написать знак перпендикулярности

Пишем символы на клавиатуре

Иногда возникает ситуация, когда вам необходимо употребить в каком-нибудь тексте специальный символ, однако на клавиатуре клавиши с таким символом не существует. Что тогда?

Существует несколько путей.
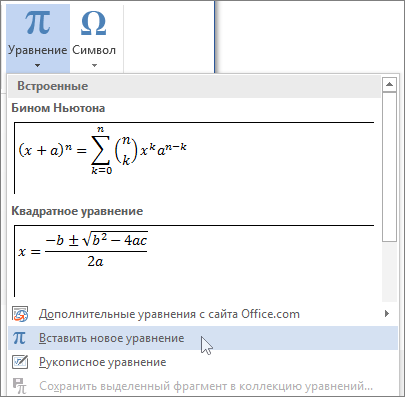
Если вы печатаете в текстовом редакторе Microsoft Word 2007, то все просто: достаточно выбрать на закладке Вставка пункт «Символ». В раскрывшемся списке выбираете нужный символ либо нажимаете на Другие символы… В открывшемся диалоговом окне находите необходимый символ и нажимаете клавишу Вставить.

А как поступить с другими редакторами или поисковиками?
Вот коды некоторых символов.
●Пошагово:
1.Включаем кнопку NumLock(в правой части клавиатуры)
2. Зажимаем Alt.
3. И одновременно с зажатой клавишей alt Набираем на цифровом блоке комбинацию.
4. Отжимаем Alt.
4. Любуемся значком.

Еще символы:
© Копирайт [0169]♥ Сердечко [3]® Зарезервировано [0174]℠ Знак обслуживания [8480]℃ Цельсий [8451]℅ C/о [8453]℉ Фаренгейт [8457]№ Номерной знак [8470]℗ Копирайт записи [8471]℞ Фармацевтический символ [8478]Ω Ом [8486]℧ Перевернутый Ом [8487]☀ Солнце [9728]☁ Туча [9729]☂ Зонтик [9730]☃ Снеговик [9731]☄ Комета [9732]★ Звезда (закрашенная) [9733]☆ Звезда (контуры) [9734]☇ Молния [9735]☈ Гроза [9736]☉ Солнце (контур) [9737]☊ Восходящий узел [9738]☋ Нисходящий узел [9739]☌ Сопряжение [9740]☍ Оппозиция [9741]☎ Телефон (закрашенный) [9742]☏ Телефон (контур) 9743]☐ Пустой квадрат [9744]☑ Квадратик с галочкой [9745]☒ Квадратик с крестиком X [9746]☓ Андреевский крест [9747]☚ Палец, показывающий налево (закрашенный) [9754]☛ Палец, показывающий направо (закрашенный) [9755]☜ Палец, показывающий налево (контур) [9756]☝ Палец, показывающий вверх (контур) [9757]☞ Палец, показывающий направо (контур) [9758]☟ Палец, показывающий вниз (контур) [9759]☠ Череп и кости [9760]☡ Предупреждающий знак [9761]☢ Знак радиации [9762]☣ Знак биологической опасности [9763]☤ Кадуцей (жезл Гермеса) [9764]☥ Анкх [9765]☦ Восточно-христианский крест [9766]☧ Христограмма [9767]☨ Патриархальный крест [9768]☩ Греческий крест [9769]☪ Луна и звезда [9770]☫ Символ Фарси [9771]☬ Ади Шакти [9772]☭ Серп и молот [9773]☮ Знак мира [9774]☯ Инь и Янь [9775]☰ Триграмма небо [9776]☱ Триграмма озеро [9777]☲ Триграмма огонь [9778]☳ Триграмма гроза [9779]☴ Триграмма ветер [9780]☵ Триграмма вода [9781]☶ Триграмма гора [9782]☷ Триграмма земля [9783]☸ Колесо дхарма [9784]☹ Грустный смайл [9785]☺ Веселый смайл [9786]☻ Черный смайл [9787]☽ Растущая луна [9789]☾ Спадающая луна [9790]☿ Меркурий [9791]♀ Венера (знак женщины) [9792]♁ Земля [9793]♂ Марс (знак мужчины) [9794]♃ Юпитер [9795]♄ Сатурн [9796]♅ Уран [9797]♆ Нептун [9798]♇ Плутон [9799]♈ Овен [9800]♉ Телец [9801]♊ Близнецы [9802]♋ Рак [9803]♌ Лев [9804]♍ Дева [9805]♎ Весы [9806]♏ Скорпион [9807]♐ Стрелец [9808]♑ Козерог [9809]♒ Водолей [9810]♓ Рыбы [9811]♔ Белый король [9812]♕ Белая королева [9813]♖ Белая ладья [9814]♗ Белый слон [9815]♘ Белая лошадь [9816]♙ Белая пешка [9817]♚ Черный король [9818]♛ Черная королева [9819]♜ Черная ладья [9820]♝ Черный слон [9821]♞ Черная лошадь [9822]♟ Черная пешка [9823]♠ Черная пика [9824]♡ Черва [9825]♢ Бубна [9826]♣ Трефа [9827]♤ Пика (контур) [9828]♥ Черва (закрашенная) или сердце [9829]♦ Бубна (закрашенная) [9830]♧ Трефа (контур) [9831]♨ Гейзер [9832]♩ Музыкальная четвертная нота [9833]♪ Музыкальная восьмая нота [9834]♫ Соединенные две ноты [9835]♬ Соединенные двойной планкой две ноты [9836]♭ Бемоль [9837]♮ Звук натурального звукоряда [9838]♯ Диез [9839]✁ Отрезать сверху [9985]✂ Отрезать здесь [9986]✃ Отрезать снизу [9987]✄ Ножницы [9988]✆ Общественный телефон [9990]✇ Кассета [9991]✈ Аэропорт/самолет [9992]✉ Конверт/email [9993]✌ Знак победы [9996]✍ Подпись [9997]✎ Диагональный карандаш [9998]✏ Карандаш [9999]✐ Диагональный карандаш, смотрящий вверх [10000]✓ Галочка [10003]✔ Жирная галочка [10004]✕ Знак умножения/X [100005]✖ Жирный знак умножения/X [10006]✗ Наклоненный знак X [10007]✘ Жирный наклоненный знак X [10008]✝ Римский крест [10013]✞ Римский крест 3D [10014]✟ Латинский крест (контур) [10015]✠ Мальтийский крест [10016]✡ Звезда Давида [10017]❛ Знак кавычек [10075]❜ Знак кавычек (перевернутый) [10076]❝ Двойной знак кавычек [10077]❞ Двойной знак кавычек (перевернутый) [10078]™ Товарный знак [0153]○= 777

Не забывайте подписываться и делиться с друзьями ссылкой на наш канал. Самое интересное впереди.

Источник статьи: http://zen.yandex.ru/media/goodtip/pishem-simvoly-na-klaviature-5ba8ef802098b300aab5f80a

Значок перпендикулярности в ворде

Примечание: Мы стараемся как можно оперативнее обеспечивать вас актуальными справочными материалами на вашем языке. Эта страница переведена автоматически, поэтому ее текст может содержать неточности и грамматические ошибки. Для нас важно, чтобы эта статья была вам полезна. Просим вас уделить пару секунд и сообщить, помогла ли она вам, с помощью кнопок внизу страницы. Для удобства также приводим ссылку на оригинал (на английском языке).

В Word можно вставлять математические символы в уравнения и текст.

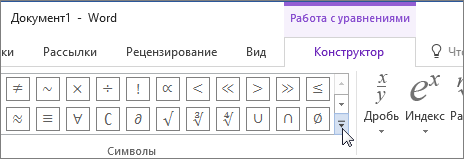
На вкладке Вставка в группе Символы щелкните стрелку рядом с надписью Формула и выберите Вставить новую формулу.

В области Работа с формулами в группе Символы на вкладке Конструктор щелкните стрелку Еще.

Щелкните стрелку рядом с названием набора символов, а затем выберите набор символов, который вы хотите отобразить.

Доступные наборы символов

В группе Символы в Word доступны указанные ниже наборы математических символов. Щелкнув стрелку Еще, выберите меню в верхней части списка символов, чтобы просмотреть группы знаков.

Основные математические символы

Часто используемые математические символы, такие как > и

Лучший ответ

Енот 8 (337417) 6 26 633 6 лет

Ответы

FighteR (30) 7 (88378) 7 26 967 6 лет

ПРОЖЕКТОР 6 (9106) 3 13 43 6 лет

радует, что у некоторых очень не плохо развито ассоциативное мышление! Причем морфологически безупречное .))

Ylarya 6 (6586) 2 4 15 6 лет

Vadinho 6 (16535) 3 41 85 6 лет

Содержание

На плоскости [ править | править код ]

Перпендикулярные прямые на плоскости [ править | править код ]

Две прямые на плоскости называются перпендикулярными, если при пересечении образуют 4 прямых угла.

Про прямую m перпендикулярную к прямой ℓ проведённую через точку P вне прямой ℓ , говорят, что m есть перпендикуляр опущенный из P на ℓ . Если же точка P лежит на прямой ℓ , то говорят, что m есть перпендикуляр к восстановленный из P к ℓ (устаревший термин восставленный [1] ).

В координатах [ править | править код ]

В аналитическом выражении прямые, заданные линейными функциями

y = a ⋅ x + b

y = k ⋅ x + m

будут перпендикулярны, если выполнено следующее условие на их угловые коэффициенты

a ⋅ k = − 1.

Построение перпендикуляра [ править | править код ]

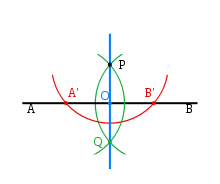
Шаг 1: С помощью циркуля проведём полуокружность с центром в точке P, получив точки А и В.

Шаг 2: Не меняя радиуса, построим две полуокружности с центром в точках A и В соответственно, проходящими через точку P. Кроме точки P есть ещё одна точка пересечения этих полуокружностей, назовём её Q.

Шаг 3: Соединяем точки P и Q. PQ и есть перпендикуляр к прямой AB.

Координаты точки основания перпендикуляра к прямой [ править | править код ]

Пусть прямая задаётся точками A ( x a , y a ) и B ( x b , y b ) . На прямую опускается перпендикуляр из точки P ( x p , y p ) . Тогда основание перпендикуляра O ( x o , y o ) ,y_ )> можно найти следующим образом.

Если x a = x b (вертикаль), то x o = x a =x_> и y o = y p =y_

> . Если y a = y b (горизонталь), то x o = x p =x_

> и y o = y a =y_> .

Во всех остальных случаях:

x o = x a ⋅ ( y b − y a ) 2 + x p ⋅ ( x b − x a ) 2 + ( x b − x a ) ⋅ ( y b − y a ) ⋅ ( y p − y a ) ( y b − y a ) 2 + ( x b − x a ) 2 = +x_

-y_)> +(x_-x_)^ >>> ; y o = ( x b − x a ) ⋅ ( x p − x o ) ( y b − y a ) + y p = -x_)cdot (x_

> .

В трёхмерном пространстве [ править | править код ]

Перпендикулярные прямые [ править | править код ]

Две прямые в пространстве перпендикулярны друг другу, если они соответственно параллельны некоторым двум другим взаимно перпендикулярным прямым, лежащим в одной плоскости. Две прямые, лежащие в одной плоскости, называются перпендикулярными (или взаимно перпендикулярными), если они образуют четыре прямых угла.

Перпендикулярность прямой к плоскости [ править | править код ]

Определение: Прямая называется перпендикулярной к плоскости, если она перпендикулярна всем прямым, лежащим в этой плоскости.

Признак: Если прямая перпендикулярна двум пересекающимся прямым плоскости, то она перпендикулярна этой плоскости.

Плоскость, перпендикулярная одной из двух параллельных прямых, перпендикулярна и другой. Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.

Перпендикулярные плоскости [ править | править код ]

Две плоскости называются перпендикулярными, если двугранный угол между ними равен 90°.

Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
Если из точки, принадлежащей одной из двух перпендикулярных плоскостей, провести перпендикуляр к другой плоскости, то этот перпендикуляр полностью лежит в первой плоскости.
Если в одной из двух перпендикулярных плоскостей провести перпендикуляр к их линии пересечения, то этот перпендикуляр будет перпендикулярен второй плоскости.
Плоскость, перпендикулярная двум пересекающимся плоскостям, перпендикулярна их линии пересечения [2] .

В многомерных пространствах [ править | править код ]

Перпендикулярность плоскостей в 4-мерном пространстве [ править | править код ]

Перпендикулярность плоскостей в четырёхмерном пространстве имеет два смысла: плоскости могут быть перпендикулярны в 3-мерном смысле, если они пересекаются по прямой (а следовательно, лежат в одной гиперплоскости), и двугранный угол между ними равен 90°.

Плоскости могут быть также перпендикулярны в 4-мерном смысле, если они пересекаются в точке (а следовательно, не лежат в одной гиперплоскости), и любые 2 прямые, проведённые в этих плоскостях через точку их пересечения (каждая прямая в своей плоскости), перпендикулярны.

В 4-мерном пространстве через данную точку можно провести ровно 2 взаимно перпендикулярные плоскости в 4-мерном смысле (поэтому 4-мерное евклидово пространство можно представить как декартово произведение двух плоскостей). Если же объединить оба вида перпендикулярности, то через данную точку можно провести 6 взаимно перпендикулярных плоскостей (перпендикулярных в любом из двух вышеупомянутых значений).

Существование шести взаимно перпендикулярных плоскостей можно пояснить таким примером. Пусть дана система декартовых координат x y z t. Для каждой пары координатных прямых существует плоскость, включающая эти две прямые. Количество таких пар равно ( 4 2 ) = 6 >=6> : xy, xz, xt, yz, yt, zt, и им соответствуют 6 плоскостей. Те из этих плоскостей, которые включают одноимённую ось, перпендикулярны в 3-мерном смысле и пересекаются по прямой (например, xy и xz, yz и zt), а те, которые не включают одноимённых осей, перпендикулярны в 4-мерном смысле и пересекаются в точке (например, xy и zt, yz и xt).

Перпендикулярность прямой и гиперплоскости [ править | править код ]

Пусть задано n-мерное евклидово пространство R n ^ > (n>2) и ассоциированное с ним векторное пространство W n > , а прямая l с направляющим векторным пространством L 1 > и гиперплоскость Π k > с направляющим векторным пространством L k > (где L 1 ⊂ W n subset W^ > , L k ⊂ W n , k n subset W^ , k ) принадлежат пространству R n ^ > .

Прямая l называется перпендикулярной гиперплоскости Π k > , если подпространство L 1 > ортогонально подпространству L k > , то есть ( ∀ a → ∈ L 1 ) ( ∀ b → ∈ L k ) a → b → = 0 in L_ ) (forall in L_ ) =0>

Источник статьи: http://pcznatok.ru/kompjutery/znachok-perpendikuljarnosti-v-vorde.html