Калькулятор Интегралов
Вычисление интегралов онлайн
— по шагам и с графиками!
Калькулятор Интегралов позволяет вычислять интегралы и первообразные функций онлайн — совершенно бесплатно!
Наш Калькулятор позволяет проверить решение Ваших математических заданий. Он поможет вам с решением задачи показывая весь ход решения шаг за шагом. Поддерживаются все виды интегрирования включая специальные функции.
Калькулятор Интегралов поддерживает вычисление определённых и неопределённых (первообразных функций) интегралов включая интегрирование функций с несколькими переменными. Кроме этого Вы можете проверить результат своего решения! Интерактивные графики помогут представить и лучше понять функции интегралов.
Чтобы узнать больше о том как пользоваться Калькулятором Интегралов, загляните в раздел «Справка» или ознакомьтесь с примерами.
Ну что ж, теперь — вперед! Успешного интегрирования!
Введите функцию, которую вы хотите проинтегрировать в Калькулятор Интегралов. Не вводите «f(x) =» часть! Калькулятор Интегралов сразу показывает математическое выражение в графическом виде, прямо в процессе ввода. Убедитесь, что это выражение соответствует тому, что Вы хотели ввести. Используйте скобки если понадобится, например «a/(b+c)«.
В разделе «Примеры», приведены некоторые из функций которые Калькулятор Интегралов способен вычислять.
После того как Вы закончили вводить вашу функцию, нажмите «=» и Калькулятор Интегралов выдаст результат.
В разделе «Настройки» переменная интегрирования и пределы интегрирования могут быть установлены/изменены. Если пределы интегрирования не будут указаны, то будет вычислена только лишь первообразная функция.
Щелчок мышки на примере вводит его в Калькулятор Интегралов. Простое наведение мышки — показывает текст выражения.
Настройте параметры калькулятора:
| Переменная интегрирования: | |
|---|---|
| Верхний предел (до): | 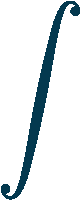 +∞ +∞ |
| Нижний предел (от): | –∞ |
| Использовать только численное интегрирование? | |
| Упрощать выражения интенсивнее? | |
| Упрощать все корни? (√ x² станет x, а не |x|) | |
| Использовать комплексные числа (ℂ)? | |
| Использовать числа с запятой вместо дробей? |
Генератор заданий для тренировки позволяет сгенерировать сколько угодно различных случайных заданий.
Ниже Вы найдете настройки конфигурации и один из предложенных вариантов задания. Вы можете взяться за его решение (тогда оно будет введено в Калькулятор) или сгенерировать новое.
Вычисляем интеграл: Введите Ваш результат:
Следующее выражение будет вычислено:
Загрузка … пожалуйста подождите!
Это займет несколько секунд.
Это не то, что Вы имели ввиду? Используйте скобки! В случае необходимости, выберите переменную и пределы интегрирования в разделе «Настройки«.
Результаты вычислений
Как работает Калькулятор Интегралов
Для тех кому интересны технические подробности, в этой части рассказывается как устроен и работает Калькулятор Интегралов.
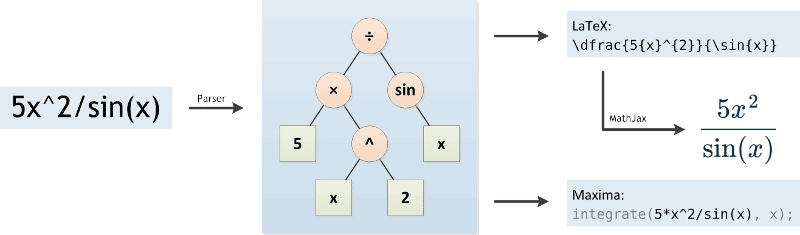
Сначала синтаксический анализатор (па́рсер) анализирует исходное математическое выражение. Он преобразует его в форму более удобную для компьютера, а именно в форму дерева (см. картинку ниже). В процессе такого преобразования, Интегральный Калькулятор должен соблюдать порядок операций с учетом их приоритета. Так же, как и то, что в математических выражениях знак умножения часто опускается, например, мы обычно пишем «5x» вместо «5*x». Калькулятор Интегралов должен уметь понимать такие случаи и сам добавлять знак умножения.
Па́рсер написан на JavaScript, и основывается на алгоритме сортировочной станции, поэтому может исполняться прямо в браузере. Это дает возможность генерировать удобочитаемое выражение на ходу, преобразуя получающееся дерево в код для LaTeX (Ла́тех). С помощью MathJax происходит генерация картинки и ее отображение в браузере.
По нажатию кнопки «=», Калькулятор Интегралов отправляет математическое выражение вместе с параметрами (переменной интегрирования и пределами интегрирования) на сервер, где оно анализируется еще раз. В этот раз выражение преобразуется в форму которая будет понятна системе компьютерной алгебры Maxima (Ма́ксима).
Ма́ксима вычисляет интеграл математической функции. Результат Ма́ксимы снова преобразуется в Ла́тех а затем показывается пользователю. Первообразная вычисляется с помощью алгоритма Ри́ша, который достаточно замысловат для понимания человеком. Именно поэтому задача показывать промежуточные шаги решения интегралов является такой сложной.
Для того чтобы всё-таки показать пошаговое решение, Калькулятор Интегралов использует такие же методы, которыми бы воспользовался человек. Алгоритм, который это осуществляет, разрабатывался в течении нескольких лет и был написан на собственном языке программирования Ма́ксимы. Программа содержит более чем 17000 строк кода. Если интегрируемое выражение совпадает по форме с уже известным, алгоритм применяет заранее определённые правила для решения интеграла (например, метод неопределённых коэффициентов для рациональных функций, тригонометрическую подстановку в интегралах с квадратным корнем из квадратичной функции или интегрирование по частям для продуктов определенных функций). Если же оно не совпадает с уже известным, тогда алгоритм пробует разные подстановки и преобразования пока интеграл не будет решен или пока не закончится отведённое для этого время или же пока не кончатся все возможные варианты. С одной стороны, у Калькулятора нет математической интуиции, которая бы очень помогла в поисках первообразной, но зато, с другой стороны, Калькулятор в состоянии перепробовать большое количество разных вариантов за очень короткое время. Такое пошаговое вычисление первообразной по правилам, зачастую, более компактно и элегантно чем вычисленное Ма́ксимой.
Еще один режим работы «Проверка решения» должен решить сложную задачу по определению являются ли два математических выражения равными друг другу. Разница между выражениями вычисляется и упрощается с помощью Ма́ксимы настолько, насколько это возможно. К примеру, это может быть переписывание тригонометрических/гиперболических функций в их экспоненциальные формы. Если удается упростить разницу до нуля — задача выполнена. В противном случае, применяется вероятностный алгоритм, который вычисляет и сравнивает оба выражения в случайно выбранных местах. В случае с первообразной, вся процедура повторяется для каждой производной, т.к. первообразная может отличаться константой.
Интерактивные графики функций вычисляются в браузере и отрисовываются на Сanvas («Холст») из HTML5. Для каждой математической функции, которая должна быть отрисована, Калькулятор создает функцию JavaScript, которая затем вычисляется с шагом, необходимым для правильного отображения графика. Все сингулярности (например полюса) функции обнаруживаются в процессе отрисовки и обрабатываются отдельно. Управление жестами для мобильных устройств сделано на основе hammer.js.
Если у Вас есть вопросы или пожелания, а так же идеи как улучшить Калькулятор Интегралов, пожалуйста пишите мне на e-mail.
© David Scherfgen 2020 — all rights reserved.
Источник статьи: http://www.integral-calculator.ru/
Неопределенный интеграл
Неопределенный интеграл онлайн
В школе говорят, интеграл – это значок ∫, а вычисление интеграла, то есть процесс интегрирования, – это операция обратная дифференцированию. Согласитесь скучно!
Разумеется, у школьников возникает резонный вопрос: а нафиг он нам нужен?
Но если бы учитель уделил несколько минут на вводную про интегралы, такой вопрос всё равно бы возник, но уже не у всех!
В далеком 17 веке были на тот момент нерешенные насущные проблемы, а именно изучались закономерности движения тел. Много трудов было проделано Ньютоном, чтобы понять, как вычисляется скорость тела в любой момент времени. Но чем дальше, тем оказалось интереснее.
Допустим, мы знаем закон изменения скорости тела – это некая функция. Тогда площадь фигуры, ограниченная этой кривой и осью координат, будет равна пройденному пути. Вычисляя неопределенный интеграл от функции, мы как раз находим общий закон движения.
В этом заключается один из физических смыслов интеграла.
Как вы уже поняли, геометрический смысл интеграла – это площадь криволинейной трапеции. Соответственно с помощью кратного интеграла вычисляется объем тела.
Лейбниц и Ньютон заложили основы дифференциального и интегрального исчисления. В последующие десятилетия было много великих открытий, связанных с вычислением интегралов.
Поскольку подынтегральная функция может принимать различные виды, естественно это привело к разделению интегралов на свои типы, а главное были отрыты многочисленные методы решения интегралов.
Но не все так безоблачно. На практике часто происходит так, что в аналитическом виде вычислить интегралы невозможно, то есть используя какой-либо известный метод. Конечно, получить аналитическое решение это здорово, но, с другой стороны, главное ведь вычислить точное значение интеграла. В этом случае интегралы решаются численными методами. Благодаря компьютерным мощностям, такие задачи не представляют особых сложностей для современного человека.
Калькулятор решения интегралов
Теперь самое интересное. Еще каких-то 15 лет назад школьник и помыслить не мог, что под рукой будут такие калькуляторы интегралов, как, например, наш. Это безусловно облегчает процесс обучения. Можно проверять свои решения, находить допущенные ошибки и лучше усваивать образовательный курс.
И тут в который раз повторяем, калькулятор решения интегралов – это только ваш безотказный помощник, к которому можете обратиться в любое время. Но никак не подмена вашей головы. Старайтесь самостоятельно решать задачи, только так можно развивать мышление, а компьютер будет в помощь.
Источник статьи: http://math24.biz/integral
Правила ввода математических выражений
Ввод чисел:
Целые числа вводятся обычным способом, например: 4 ; 18 ; 56
Для ввода отрицательного числа необходимо поставить знак минус: -19 ; -45 ; -90
Рациональные числа вводятся с использованием символа / , например: 3 / 4 ; -5 / 3 ; 5 / (-19)
Вещественные числа вводятся с использованием точки в качестве разделителя целой и дробной частей: 4.5 ; -0.4
Ввод переменных и констант:
Переменные и константы вводятся латинскими буквами, например: x ; y ; z ; a ; b .
Константы π и e вводятся как pi и e — соответственно.
Символ бесконечности ∞ вводится двумя маленькими латинскими буквами oo или словом inf .
Соответственно, плюс бесконечность задается как +oo, и минус бесконечность как -oo.
Сумма и разность:
Сумма и разность задаются при помощи знаков + и — соответственно, например: 3 + a ; x + y ; 5 — 4 + t ; a — b + 4 ; ВНИМАНИЕ! Никаких пробелов между операндами быть не должно, например ввод: x + a — неправильный , правильно вводить так: x + a — без пробелов.
Умножение:
Умножение задается знаком * , например: 3 * t ; x * y ; -5 * x .
ВНИМАНИЕ! Ввод знака * необходим всегда, т.е. запись типа: 2 x — недопустима . Следует всегда использовать знак * , т.е правильная запись: 3 * x .
Деление:
Деление задается знаком / , например: 15 / a ; y / x ;.
Степень:
Степень задается знаком ^ , например: x ^ 2 ; 4 ^ 2 ; y ^ (-1 / 2) .
Приоритет операций:
Для указания (или изменения) приоритета операций необходимо использовать скобки () , например: ( a + b ) / 4 — тут вначале будет произведено сложение a + b , а потом сумма разделится на 4 , тогда как без скобок: — сначала b разделится на 4 и к полученному прибавится a . ВНИМАНИЕ! В непонятных случаях лучше всегда использовать скобки для получения нужного результата, например: 2 ^ 4 ^ 3 — неясно как будет вычислено это выражение: cначала 2 ^ 4 , а затем результат в степень 3 , или сначала 4 ^ 3 = 64 , а затем 2 ^ 64 ? Поэтому, в данном случае, необходимо использовать скобки: (2 ^ 4) ^ 3 или 2 ^ (4 ^ 3) — смотря что нужно.
Также распространенной ошибкой является запись вида: x ^ 3 / 4 — непонятно: вы хотите возвести x в куб и полученное выражение разделить на 4 , или хотите возвести x в степень 3 / 4 ? В последнем случае необходимо использовать скобки: x ^ (3 / 4) .
Ввод функций:
Функции вводятся с использованием маленьких латинских букв: sin ; cos ; tan ; log .
ВНИМАНИЕ! Аргумент функции всегда берется в скобки () , например: sin( 4 ) ; cos( x ) ; log( 4 + y ) .
Запись типа: sin 4 ; cos x ; log 4 + y — недопустима . Правильная запись: sin( 4 ) ; cos( x ) ; log( 4 + y ) .
Если необходимо возвести функцию в степень, например: синус x и все это в квадрате, это записывается вот так: (sin( x )) ^ 2 . Если необходимо возвести в квадрат аргумент, а не функцию (т.е синус от x ^ 2 ), тогда это выглядит вот так: sin( x ^ 2) . Запись типа: sin ^ 2 x — недопустима .
Источник статьи: http://mathforyou.net/online/input/simple/
Как вводить данные? Правила ввода
Ввод данных, наверное, это самое главное, что необходимо усвоить при работе с математическими калькуляторами по решению задач. Не важно какие сервисы вы используете, будь то сайт, десктопная программа или мобильное приложение, ведь именно с корректного ввода данных начинается постановка задачи для вычислительной системы.
Как правило у каждого подобного сервиса свой синтаксис. Но какими бы ни были современные математические калькуляторы (программы), в любом случае все они базируются на принципах обработки, которые появились еще в прошлом веке. Отличаются лишь методы обработки (парсинг математических выражений), но математические формулы от этого, разумеется, не меняются.
Стоит отметить, что калькуляторы на Math24.biz куда более «умнее», или, иными словами, менее требовательны, чем ряд других аналогичных калькуляторов на просторах интернета.
Итак, начнем. Самые элементарные правила как вводить данные касаются записи чисел и скобок.
Скобки используются круглые. Но даже если вы введете [, ], <или >, то они преобразуются в соответствующие круглые. Кстати, это небольшое наше преимущество в отличие от других калькуляторов.
Что касается натуральных или дробных чисел, то тут все очевидно — «Как вижу, так и пишу!».
Обратим внимание на записи десятичных чисел и некоторых математических констант. В десятичной записи числа необходимо использовать точку, а не запятую.
Примеры ввода десятичных чисел
Такое правило ввода данных оправдывается тем, что запятая используется в функциях, например, логарифмических, в которых разделены через запятую основание логарифма и число, от которого берется логарифм. И таких функций множество, включая функции нескольких переменных.
Примеры обозначений математических констант
pi — Число Пи
e — Экспонента (основание натурального логарифма)
i — Мнимая единица, i 2 = -1
Корень квадратный от числа записывается как sqr или sqrt.
Примеры записи квадратного корня
sqrt(2) — корень квадратный из числа 2
sqrt(3/4) — корень квадратный из дробного числа ¾
Наверняка многие сейчас подумали, что квадратный корень из 2 можно записать как 2^(1/2) или 2^(0.5). Но в данном случае мы хотим лишь сказать, что sqrt есть обозначение квадратного корня, которое используется во многих программах.
Примите это на заметку, если ранее не встречались с этим обозначением!
Далее быстро пройдемся по математическим операциям и правилам их ввода, потому что здесь всё проще-простого.
+ Операция сложения (суммирование)
− Операция вычитания (разность)
* Операция умножения
Кстати, если два множителя записать через пробел, то калькулятор воспримет это за знак умножения. Например, x y равносильно x*y
/ Операция деления
^ Возведение в степень
Чуть сложнее для визуального восприятия, но никак не для понимания, это правило записи дробных выражений. Как вводить данные от таких выражений мы покажем на примерах с применением различных цветов.
Это позволит лучше и быстрее освоить необходимые навыки юным ученикам. Хотя, поверьте нам, старшеклассники и студенты очень часто сталкиваются с проблемой ввода сложных формул.
Примеры ввода дробных выражений
Для лучшего визуального восприятия мы специально добавили пробелы, чтобы выделить отдельные операции.



Как вы могли заметить, одним из базовых правил при вводе данных является использование букв только латинского алфавита!
Ниже перечислим наиболее часто встречающиеся функции при изучении школьной математики и математических дисциплин начальных курсов ВУЗов и других учебных заведений.
Источник статьи: http://math24.biz/article?id=kak_vvodit_dannyye