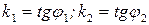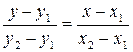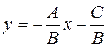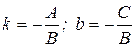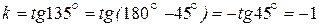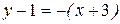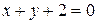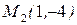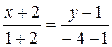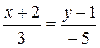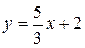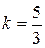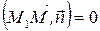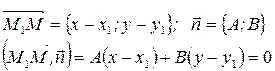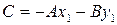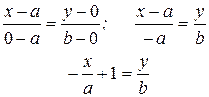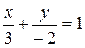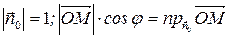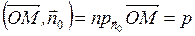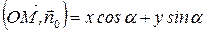Уравнение прямой с угловым коэффициентом.



Прямая линия на плоскости.
Различные уравнения прямой на плоскости.
Определение. Уравнение прямой – это уравнение, связывающее координаты
 |
x и y любой точки, лежащей на прямой.
Уравнение прямой с угловым коэффициентом.
Определение. Угловым коэффициентом прямой называется тангенс угла наклона этой прямой к оси ОХ.
Угловой коэффициент обозначается через k.
Итак,
Итак, угловой коэффициент обозначается 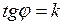
Если j- острый угол, то k>0, если j- тупой угол, то k
Запишем полученное уравнение в виде:
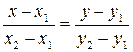
Это и есть искомое уравнение прямой, проходящей через две точки.
Уравнение вида Ax+By+C=0 (4) называется общим уравнением прямой.
а). Пусть 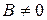
Это и есть уравнение прямой с угловым коэффициентом, т.е. уравнение
вида 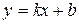
Так как уравнение (1) есть уравнение прямой, то и уравнение (4) есть также уравнение прямой.
б). Если В=0, мы получаем 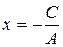
Рассмотрим примеры.
1). Написать уравнение прямой, проходящей через точку 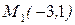
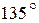
Решение. Найдем угловой коэффициент искомой прямой:
Тогда искомое уравнение примет вид
или
2). Написать уравнение прямой, проходящей через две точки: 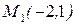
Решение. Искомое уравнение будет
или
3). Найти угловой коэффициент прямой 5x-3y+6=0.
Решение. Запишем уравнение прямой в виде уравнения прямой с угловым коэффициентом:
откуда
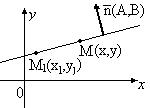
5. Уравнение прямой, проходящей через данную точку, перпендикулярно данному вектору.
Дана точка 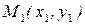
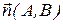
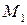
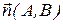
Пусть 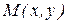
Очевидно, что векторы 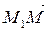
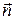
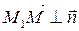
Условие перпендикулярности двух векторов – это равенство нулю их скалярного произведения:
Итак, получаем уравнение 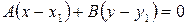
Уравнение (5) можно записать в виде Ax+By+C=0,
где
Таким образом, коэффициенты А и В в общем уравнении прямой являются координатами вектора, перпендикулярного к этой прямой. Вектор 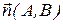
Пример. Написать уравнение прямой, проходящей через точку 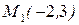
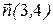
Решение. Используем уравнение (5) 3(x+2)+4(y-3)=0
6. Уравнение прямой в отрезках на осях.
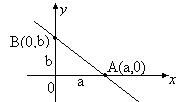
Заданная прямая проходит через две точки A(a,0) и B(0,b). Используем уравнение прямой, проходящей через две точки:
Окончательно, получаем 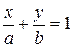
Пример. Дана прямая 2x-3y-6=0. Привести это уравнение к уравнению в отрезках на осях.
Чтобы получить отрезок a, отсекаемый на оси ОХ, нужно положить в данном уравнении y=0; чтобы получить отрезок b – х=0.
Искомое уравнение примет вид:
7. Нормальное уравнение прямой.
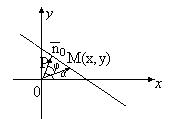
Пусть известно расстояние р от прямой до начала координат , и угол α, образуемый перпендикуляром к прямой и положительным направлением оси ОХ. Требуется написать уравнение прямой.
Пусть 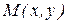
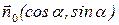
Найдем скалярное произведение 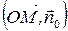
По определению скалярного произведения:
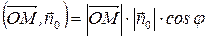
где 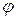
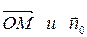
Но
Следовательно, мы получим
Итак, мы получаем уравнение 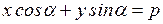
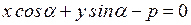
Источник статьи: http://studopedia.ru/12_139015_uravnenie-pryamoy-s-uglovim-koeffitsientom.html
Уравнение прямой с угловым коэффициентом
Прямая, проходящая через данную точку в направлении, заданном угловым коэффициентом
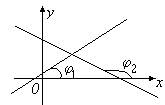
Пусть на плоскости xOy задана прямая, непараллельная оси Oy. Углом 
Если прямая параллельна оси или совпадает с нею, то угол 
Для того, чтобы составить уравнение прямой, достаточно, чтобы были заданы точка 

Угловым коэффициентом прямой называется тангенс угла наклона этой прямой к оси Ox.
Уравнение прямой с угловым коэффициентом в случае нашей задачи составляется по формуле
где 


После подстановки указанных выше величин в формулу должно получиться уравнение вида
Пример 1. Составить уравнение прямой с угловым коэффициентом, если угловой коэффициент 

Решение. Используя формулу (1), получаем:
Получили уравнение вида (2).
Проверяем — подставляем координаты точки в полученное уравнение, в нашем случае получается верное равенство:
Пример 2. Составить уравнение прямой с угловым коэффициентом, если угол наклона прямой 

Решение. Находим угловой коэффициент, то есть тангенс угла наклона прямой:
Теперь, используя формулу (1), получаем:
Получили уравнение вида (2).
Проверяем — подставляем координаты точки в полученное уравнение, в нашем случае получается верное равенство:
Решая задачи контрольных работ, надо стараться сделать проверку (для себя), даже если этого не требует условие задачи.
Как видно на примерах 1 и 2, из возможности проверки верного равенства следует возможность установить, принадлежит ли прямой, заданной уравнением с угловым коэффициентом, любая точка плоскости с заданными координатами. Проиллюстрируем это следующим примером.
Пример 3. Установить, принадлежит ли прямой, заданной уравнением с угловым коэффициентом 


Решение. Подставляя координаты точки 
Получили верное равенство, следовательно точка 
Подставляя координаты точки 
Получили неверное равенство, следовательно точка 
Прямая, проходящая через две данные точки
Применяя соотношение (1), легко решить следующую задачу: составить уравнение прямой, которая проходит через две данные точки 

В аналитической геометрии доказано, что угловой коэффициент искомой прямой можно вычислить по формуле:
Нам остаётся лишь применять эту формулу.
Пример 4. Составить уравнение прямой с угловым коэффициентом, если она проходит через точки 

Решение. По формуле (3) находим угловой коэффициент:
Теперь, используя формулу (1), получаем:
Итак, получили уравнение вида (2).
Проверяем — подставляем координаты точек в полученное уравнение, получаются верные равенства:
Прямая, проходящая через данную точку параллельно данной прямой
Для того, чтобы составить уравнение прямой, проходящей через данную точку параллельно данной прямой, следует использовать следующее условие параллельности прямых.
Для параллельности прямых необходимо и достаточно, чтобы их угловые коэффициенты были равны.
Следовательно, эта задача просто обращается в задачу из примера 1. В формулу (1) следует подставить угловой коэффициент заданной прямой.
Пример 5. Составить уравнение прямой, проходящей через точку 


Решение. Используя условия параллельности прямых. Требуется сначала найти угловой коэффициент прямой, проходящей через точки B и C, а затем воспользоваться этим угловым коэффициентом. Угловой коэффициент находим по формуле (3):
Угловой коэффициент искомой прямой также равен -5.
Теперь остаётся лишь составить уравнение прямой по угловому коэффициенту и точке, как в примере 1:
Итак, получили уравнение вида (2).
Аналогично решается задача, если задано, что прямая перпендикулярна данной прямой. Для её решения следует воспользоваться условием перпендикулярности прямых:
для перпендикулярности двух прямых необходимо и достаточно, чтобы их угловые коэффициенты были обратны по величине и противоположны по знаку.
Источник статьи: http://function-x.ru/line1.html