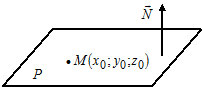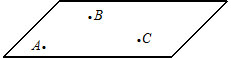Уравнение плоскости, проходящей через данную точку и параллельной заданной плоскости онлайн
С помощю этого онлайн калькулятора можно найти уравнение плоскости, проходящей через заданную точку и параллельной данной плоскости. Дается подробное решение с пояснениями. Для нахождения уравнения плоскости, введите координаты точки и коэффициенты уравнения плоскости в ячейки и нажимайте на кнопку «Решить».
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Уравнение плоскости, проходящей через данную точку и параллельной заданной плоскости − теория, примеры и решения
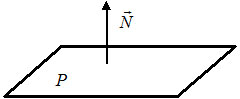
Наша задача найти уравнение плоскости, проходящей через точку M0 и параллельной плоскости (1)(Рис.1).
 |
Все параллельные плоскости имеют коллинеарные нормальные векторы. Поэтому для построения параллельной к (1) плоскости, проходящей через точку M0(x0, y0, z0) нужно взять в качестве нормального вектора искомой плоскости, нормальный вектор n=(A, B, C) плоскости (1). Далее нужно найти такое значение D, при котором точка M0(x0, y0, z0) удовлетворяла уравнению плоскости (1):
Подставляя значение D из (3) в (1), получим:
Уравнение (4) можно представить также в следующем виде:
Уравнение (5) является уравнением плоскости, проходящей через точку M0(x0, y0, z0) и параллельной плоскости (1).
Найти уравнение плоскости, проходящей через точку M0(1, −6, 2) и параллельной плоскости :
Запишем коэффициенты нормального вектора плоскости (6):
Подставляя координаты точки M0 и координаты нормального вектора в (3), получим:
Подставляя значения A, B, C, D в уравнение плоскости (1), получим:
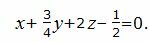 |
Уравнение плоскости можно представить в более упрощенном виде, умножив на 4:
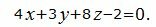 |
Уравнение плоскости, проходящей через точку M0(1, −6, 2) и параллельной плоскости (6) имеет следующий вид:
Источник статьи: http://matworld.ru/analytic-geometry/uravnenie-ploskosti2-online.php
Уравнение плоскости, проходящей через точку параллельно плоскости
Уравнение плоскости, проходящей через точку параллельно плоскости, задаётся равенством нулю скалярного произведения вектора-разности радиусов-векторов точек и нормали к плоскости.
Содержание
[править] Обозначения
[math]\bar r=(x,y,z)[/math] — радиус-вектор точки плоскости; [math]\bar r_0=(x_0,y_0,z_0)[/math] — радиус-вектор точки; [math]\bar n_1=(A_1,B_1,C_1)[/math] — нормаль к плоскости; [math]A_1x+B_1y+C_1z+D_1=0[/math] — уравнение плоскости.[править] Формулы:
Векторная форма: [math]\left(\left(\bar r — \bar r_0\right)\cdot \bar n_1\right)=0 \Leftrightarrow \left(\bar r \cdot \bar n_1\right)-\left(\bar r_0 \cdot \bar n_1\right)=0[/math] [math]A_1(x-x_0)+B_1(y-y_0)+C_1(z-z_0)=0 \Leftrightarrow[/math] [math]\Leftrightarrow A_1x+B_1y+C_1z-(A_1x_0+B_1y_0+C_1z_0)=0[/math]
[править] Уравнения плоскости:
[править] Литература
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров — М.: Наука, 1970.
- Выгодский М. Я. Справочник по высшей математике — М.: Наука, 1964, стр.162.
Персональные инструменты
Пространства имён
Варианты
Просмотры
Действия
Поиск
Навигация
Инструменты
Текст страницы доступен по условиям лицензии GNU Free Documentation License. Материалы могут быть скопированы при условии указания активной ссылки на источник копирования в теле статьи (на той же странице). В отдельных случаях могут действовать условия лицензии Creative Commons Attribution-ShareAlike (CC BY-SA 3.0), информацию об этом можно просмотреть на странице обсуждения или в истории правок. В частности, условия лицензии CC BY-SA 3.0 действуют в отношении статей, перенесенных из Википедии (указание на факт переноса всегда есть в истории правок статьи).
- Политика конфиденциальности
- Описание Циклопедии
- Отказ от ответственности
Математический портал
Nav view search
Navigation
Search
- Вы здесь:
- Home
- Аналитическая геометрия
- Плоскость в пространстве, всевозможные уравнения, расстояние от точки до плоскости.
Плоскость в пространстве, всевозможные уравнения, расстояние от точки до плоскости.
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Существуют такие формы записи уравнения плоскости:
1) $Ax+By+Cz+D=0 -$ общее уравнение плоскости $P,$ где $\overline
2) $A(x-x_0)+B(y-y_0)+C(z-z_0)=0 -$ уравнение плоскости $P,$ которая проходит через точку $M(x_0, y_0, z_0)$ перпендикулярно вектору $\overline
4) $\begin
5) $x\cos\alpha+y\cos\beta+z\cos\gamma-p=0 -$ нормальное уравнение плоскости, где $\cos\alpha, \cos\beta$ и $\cos\gamma -$ направляющие косинусы нормального вектора $\overline
Общее уравнение плоскости приводится к нормальному, путем умножения на нормирующий множитель $\mu=-\frac
Расстояние от точки $M(x_0, y_0, z_0)$ до плоскости $P: Ax+By+Cz+D=0$ вычисляется по формуле $$d=\left|\frac
а) Заданы плоскость $P: -2x+y-z+1=0$ и точка $M(1, 1, 1).$ Написать уравнение плоскости $P’,$ проходящей через точку $M$ параллельно плоскости $P$ и вычислить расстояние $\rho(P, P’).$
Так как п.лоскости $P$ и $P’$ параллельны, то нормальный вектор для плоскости $P$ будет также нормальным вектором для плоскости $P’.$ Из уравнения плоскости получаем $\overline
Далее запишем уравнение плоскости по формуле ( 2): $A(x-x_0)+B(y-y_0)+C(z-z_0)=0 -$ уравнение плоскости, которая проходит через точку $M(x_0, y_0, z_0)$ перпендикулярно вектору $\overline
Ответ: $-2x+y-z+2=0.$
а) Написать уравнение плоскости $P’,$ проходящей через заданные точки $M_1(1, 2, 0)$ и $M_2(2, 1, 1)$ перпендикулярно заданной плоскости $P: -x+y-1=0.$
Из уравнения плоскости $P,$ находим ее нормальный вектор $\overline
Поскольку $z_N=0,$ то есть вектор $N\in XoY,$ то $z_
Так как точка $M_1\in P’,$ то и $M_3\in P’.$ Запишем уравнение плоскости, которая проходит через три точки $M_1 (1, 2, 0), M_2(2, 1, 1)$ и $M_3(2, 1, 0).$
$(x-1)(-1)0+(-1)z+(y-2)-(-1)z-(-1)(x-1)-(y-2)0=0\Rightarrow$ $\Rightarrow-z+y-2+z+x-1=0\Rightarrow x+y-3=0.$
а) Написать уравнение плоскости $P,$ проходящей через точку $M(1, 1, 1)$ параллельно векторам $a_1(0, 1, 2)$ и $a_2(-1, 0, 1).$
Поскольку вектор $[a_1, a_2]$ перпендикулярен плоскости векторов $a_1$ и $a_2$ (см. векторное произведение), то он будет также перпендикулярен искомой плоскости. То есть вектор $[a_1, a_2]$ является нормальным для плоскости $P.$ Найдем этот вектор:
Таким образом $\overline
Теперь можно найти уравнение плоскости $P,$ по формуле (2), как плоскости, проходящей через точку $M(1, 1, 1)$ перпендикулярно вектору $\overline N=(1, -2, 1):$
Ответ: $x-2y+z=0.$
а) Написать уравнение плоскости $P,$ проходящей через точки $M_1(1, 2, 0)$ и $M_2(2, 1, 1)$ параллельно вектору $a=(3, 0, 1).$
Поскольку вектор $a$ параллелен плоскости $P,$ то для всякого вектора $\overline
Пусть $M_3=(x, y, z).$ Тогда $\overline
Из условия параллельности векторов имеем $\frac
Мы получили точку $M_3=(4, 2, 1).$
Запишем уравнение плоскости, которая проходит через три точки $M_1 (1, 2, 0), M_2(2, 1, 1)$ и $M_3(4, 2, 1).$
$(x-1)(-1)1+1\cdot z\cdot 0+(y-2)3-3(-1)z-0\cdot 1\cdot(x-1)-1(y-2)1=0\Rightarrow$
$\Rightarrow -x+1+3y-6+3z-y+2=0\Rightarrow -x+2y+3z-3=0.$
а) Написать уравнение плоскости, проходящей через три заданные точки $M_1(1, 2,0),$ $M_2(2, 1, 1)$ и $M_3(3, 0, 1).$
$\Rightarrow -x+1+-2z+2y-4+2z+2x-2-y+2=0\Rightarrow x+y-3=0.$
Источник статьи: http://mathportal.net/index.php/analiticheskaya-geometriya/ploskost-v-prostranstve-vsevozmozhnye-uravneniya-rasstoyanie-ot-tochki-do-ploskosti
Уравнение плоскости.
Общее уравнение плоскости
Любую плоскость можно задать уравнением плоскости первой степени вида
где A, B и C не могут быть одновременно равны нулю.
Уравнение плоскости в отрезках
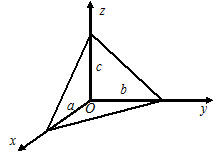
Если плоскость пересекает оси OX, OY и OZ в точках с координатами ( a , 0, 0), (0, b , 0) и (0, 0, с ), то она может быть найдена, используя формулу уравнения плоскости в отрезках
Уравнение плоскости, проходящей через точку, перпендикулярно вектору нормали
Чтобы составить уравнение плоскости, зная координаты точки плоскости M( x 0, y 0, z 0) и вектора нормали плоскости n = < A; B; C >можно использовать следующую формулу.
Уравнение плоскости, проходящей через три заданные точки, не лежащие на одной прямой
Если заданы координаты трех точек A( x 1, y 1, z 1), B( x 2, y 2, z 2) и C( x 3, y 3, z 3), лежащих на плоскости, то уравнение плоскости можно найти по следующей формуле
| x — x 1 | y — y 1 | z — z 1 | = 0 |
| x 2 — x 1 | y 2 — y 1 | z 2 — z 1 | |
| x 3 — x 1 | y 3 — y 1 | z 3 — z 1 |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Источник статьи: http://ru.onlinemschool.com/math/library/analytic_geometry/plane/
Уравнение плоскости, проходящей через данную прямую параллельно другой прямой онлайн
С помощю этого онлайн калькулятора можно построить уравнение плоскости, проходящей через прямую L1 параллельно другой прямой L2 (прямые L1 и L2 не параллельны). Дается подробное решение с пояснениями. Для построения уравнения плоскости задайте вид уравнения прямых (канонический или параметрический) введите коэффициенты уравнений прямых в ячейки и нажимайте на кнопку «Решить».
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Уравнение плоскости, проходящей через данную прямую параллельно другой прямой − теория, примеры и решения
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямые L1 и L2, которые не параллельны:
Задача заключается в построении уравнения плоскости α, проходящей через прямую L1 параллельно прямой L2(Рис.1).
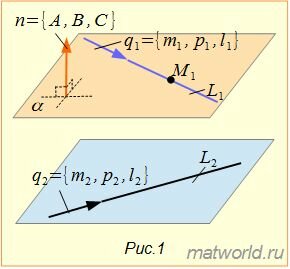 |
Прамая L1 должна лежать на искомой плоскости α, следовательно точка M1 должна нежать на плоскости α.
Уравнение плоскости можно записать формулой
и поскольку M1(x1, y1, z1) принадлежит этой плоскости, то справедливо следующее равенство:
Для того, чтобы плоскость α проходила через прямую L1, нормальный вектор плоскости n=<A, B, C> должен быть ортогональным направляющему вектору q1 прямой L1, т.е. скалярное произведение этих векторов должен быть равным нулю:
Для того, чтобы плоскость α была параллельна прямой L2, нормальный вектор плоскости n=<A, B, C> должен быть ортогональным направляющему вектору q2 прямой L2, т.е. скалярное произведение этих векторов должен быть равным нулю:
Таким образом мы должны решить систему трех уравнений с четыремя неизвестными (4)−(6). Представим систему линейных уравнений (4)−(6) в матричном виде:
Решив однородную систему линейных уравнений (7) найдем частное решение. (как решить систему линейных уравнений посмотрите на странице метод Гаусса онлайн). Подставляя полученные коэффициенты A, B, C и D в уравнение (3), получим уравнение плоскости, проходящей через прямую L1 параллельно прямой L2.
Пример 1. Найти уравнение плоскости α, проходящей через прямую L1:
паралленьно другой прямой L2 :
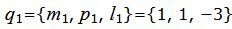 |
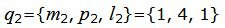 |
Поскольку плоскость проходит через прямую L1 , то она проходит также через точку M1(x1, y1, z1)=M1(1, 1, 5) и нормальный вектор плоскости n=<A, B, C> перпендикулярна направляющему вектору q1=<m1, p1, l1>= <1, 1, −3>прямой L1. Тогда уравнение плоскости должна удовлетворять условию:
а условие параллельности прямой L1 и искомой плоскости α представляется следующим равенством:
Так как плоскость α должна быть параллельной прямой L2, то должна выполнятся условие:
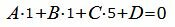 | (13) |
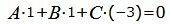 | (14) |
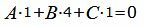 | (15) |
Представим эти уравнения в матричном виде:
Решим систему линейных уравнений (16) отностительно A, B, C, D:
Так как искомая плоскость проходит через точку M1 и имеет нормальный вектор n=<A, B, C>= <−13/24,1/6,−1/8>то она может быть представлена формулой:
Подставляя значения A,B,C,D в (17), получим:
Уравнение плоскости можно представить более упрощенном виде, умножив на число −24:
Ответ: Уравнение плоскости, проходящей через прямую (1) параллельно прямой (2) имеет вид (19).
Пример 2. Найти уравнение плоскости α, проходящей через прямую L1:
Поскольку плоскость проходит через прямую L1 , то она проходит также через точку M1(x1, y1, z1)=M1(−2, 0, 1) и нормальный вектор плоскости n=<A, B, C> перпендикулярна направляющему вектору q1=<m1, p1, l1>= <5, −8, 3>прямой L1. Тогда уравнение плоскости должна удовлетворять условию:
а условие параллельности прямой L1 и искомой плоскости α представляется следующим равенством:
Так как плоскость α должна быть параллельной прямой L2, то должна выполнятся условие:
Представим эти уравнения в матричном виде:
Решим систему линейных уравнений (28) отностительно A, B, C, D:
Так как искомая плоскость проходит через точку M1 и имеет нормальный вектор n=<A, B, C>= <11/35,2/35,−13/35>то она может быть представлена формулой:
Подставляя значения A,B,C,D в (30), получим:
Уравнение плоскости можно представить более упрощенном виде, умножив на число 35:
Ответ: Уравнение плоскости, проходящей через прямую (1) параллельно прямой (2) имеет вид (32).
Источник статьи: http://matworld.ru/analytic-geometry/uravnenie-ploskosti5-online.php