Квадратичная функция и ее график
В этой статье мы поговорим о том, что такое квадратичная функция, научимся строить ее график и определять вид графика в зависимости от знака дискриминанта и знака старшего коэффициента.
Итак.
Функция вида 


В уравнении квадратичной функции:
a — старший коэффициент
b — второй коэффициент
с — свободный член.
Графиком квадратичной функции является квадратичная парабола, которая для функции 
Обратите внимание на точки, обозначенные зелеными кружками — это, так называемые «базовые точки». Чтобы найти координаты этих точек для функции 
Внимание! Если в уравнении квадратичной функции старший коэффициент 

График функции 
Для нахождения координат базовых точек составим таблицу:
Обратите внимание, что график функции 

Если старший коэффициент a>0 , то ветви параболы напрaвлены вверх .
Если старший коэффициент a , то ветви параболы напрaвлены вниз .
Второй параметр для построения графика функции — значения х, в которых функция равна нулю, или нули функции. На графике нули функции 

Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю, чтобы найти координаты точек пересечения графика функции 

В случае квадратичной функции 

В процессе решения квадратного уравнения мы находим дискриминант: 
И здесь возможны три случая:
1. Если 




2. Если 




3 . Если 




Если 

Следовательно, зная направление ветвей параболы и знак дискриминанта, мы уже можем в общих чертах определить, как выглядит график нашей функции.
Следующий важный параметр графика квадратичной функции — координаты вершины параболы:
Прямая, проходящая через вершину параболы параллельно оси OY является осью симметрии параболы.
И еще один параметр, полезный при построении графика функции — точка пересечения параболы 
Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы 

То есть точка пересечения параболы с осью OY имеет координаты (0;c).
Итак, основные параметры графика квадратичной функции показаны на рисунке:
Рассмотрим несколько способов построения квадратичной параболы. В зависимости от того, каким образом задана квадратичная функция, можно выбрать наиболее удобный.
1. Функция задана формулой 
Рассмотрим общий алгоритм построения графика квадратичной параболы на примере построения графика функции
1. Направление ветвей параболы.
Так как 

2. Найдем дискриминант квадратного трехчлена

Дискриминант квадратного трехчлена больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ.
Для того, чтобы найти их координаты, решим уравнение:

3. Координаты вершины параболы:
4. Точка пересечения параболы с осью OY: (0;-5),и ей симметричная относительно оси симметрии параболы.
Нанесем эти точки на координатную плоскость, и соединим их плавной кривой:
Этот способ можно несколько упростить.
1. Найдем координаты вершины параболы.
2. Найдем координаты точек, стоящих справа и слева от вершины.
Воспользуемся результатами построения графика функции
Кррдинаты вершины параболы
Ближайшие к вершине точки, расположенные слева от вершины имеют абсциссы соответственно -1;-2;-3
Ближайшие к вершине точки, расположенные справа имеют абсциссы соответственно 0;1;2
Подставим значения х в уравнение функции, найдем ординаты этих точек и занесем их в таблицу:
Нанесем эти точки на координатную плоскость и соединим плавной линией:
2 . Уравнение квадратичной функции имеет вид 

или в уравнении квадратичной функции 
Построим для примера график функции 
Вспомним линейные преобразования графиков функций. Чтобы построить график функции 
- сначала построить график функции
,
- затем одинаты всех точек графика умножить на 2,
- затем сдвинуть его вдоль оси ОХ на 1 единицу вправо,
- а затем вдоль оси OY на 4 единицы вверх:
Теперь рассмотрим построение графика функции 

Выделим в уравнении функции полный квадрат:
Следовательно, координаты вершины параболы: 
3 . Уравнение квадратичной функции имеет вид y=(x+a)(x+b)
Построим для примера график функции y=(x-2)(x+1)
1. Вид уравнения функции позволяет легко найти нули функции — точки пересечения графика функции с осью ОХ:
(х-2)(х+1)=0, отсюда
2. Координаты вершины параболы:
3. Точка пересечения с осью OY: с=ab=(-2)(1)=-2 и ей симметричная.
Нанесем эти точки на координатную плоскость и построим график:
График квадратичной функции.
Перед вами график квадратичной функции вида 
Кликните по чертежу.
Подвигайте движки.
Исследуйте зависимость
— ширины графика функции 

— сдвига графика функции 


— сдвига графика функции 
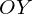

— направления ветвей параболы от знака коэффициента 
— координат вершины параболы 


И.В. Фельдман, репетитор по математике.
Источник статьи: http://ege-ok.ru/2012/05/21/kvadratichnaya-funktsiya-i-ee-grafik

































