I. Механика
Тестирование онлайн
Гармоническое колебание
Это периодическое колебание, при котором координата, скорость, ускорение, характеризующие движение, изменяются по закону синуса или косинуса.
График гармонического колебания
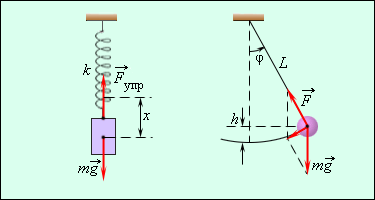
График устанавливает зависимость смещения тела со временем. Установим к пружинному маятнику карандаш, за маятником бумажную ленту, которая равномерно перемещается. Или математический маятник заставим оставлять след. На бумаге отобразится график движения.
Графиком гармонического колебания является синусоида (или косинусоида). По графику колебаний можно определить все характеристики колебательного движения.
Уравнение гармонического колебания
Уравнение гармонического колебания устанавливает зависимость координаты тела от времени
График косинуса в начальный момент имеет максимальное значение, а график синуса имеет в начальный момент нулевое значение. Если колебание начинаем исследовать из положения равновесия, то колебание будет повторять синусоиду. Если колебание начинаем рассматривать из положения максимального отклонения, то колебание опишет косинус. Или такое колебание можно описать формулой синуса с начальной фазой 
.
Изменение скорости и ускорения при гармоническом колебании
Не только координата тела изменяется со временем по закону синуса или косинуса. Но и такие величины, как сила, скорость и ускорение, тоже изменяются аналогично. Сила и ускорение максимальные, когда колеблющееся тело находится в крайних положениях, где смещение максимально, и равны нулю, когда тело проходит через положение равновесия. Скорость, наоборот, в крайних положениях равна нулю, а при прохождении телом положения равновесия — достигает максимального значения.
Если колебание описывать по закону косинуса
Если колебание описывать по закону синуса
Максимальные значения скорости и ускорения
Проанализировав уравнения зависимости v(t) и a(t), можно догадаться, что максимальные значения скорость и ускорение принимают в том случае, когда тригонометрический множитель равен 1 или -1. Определяются по формуле
Как получить зависимости v(t) и a(t)
Формулы зависимостей скорости от времени и ускорения от времени можно получить математически, зная зависимость координаты от времени. Аналогично равноускоренному движению, зависимость v(t) — это первая производная x(t). А зависимость a(t) — это вторая производная x(t).
При нахождении производной предполагаем, что переменной (то есть x в математике) является t, остальные физические величины воспринимаем как постоянные.
Источник статьи: http://fizmat.by/kursy/kolebanija_volny/garmonicheskoe
Гармонические колебания
Содержание:
Техника и окружающий мир являются примерами того, что существуют такие процессы, которые повторяются через определенные промежутки времени, то есть периодически. Их называют колебательными.
Колебательные движения. Формулы
Такие движения относят к явлениям с разной физической природой с подчинением общим закономерностям. Запись колебания тока в электрической цепи и математического маятника производится одним и тем же уравнением. Различная природа колебательных движений позволяет рассматривать их с единой точки зрения, исходя из общности закономерностей.
Механические колебания – это периодические или непериодические изменения физической величины, описывающей механическое движение (скорость, перемещение и так далее).
Когда в заданной среде атомы располагаются очень близко или молекулы испытывают силовое воздействие, наблюдается возбуждение механических колебаний. Это говорит о том, что процесс будет иметь конечную скорость, зависящую от свойств среды, которая распространяется от точки к точке. Так возникают механические волны. Явный пример – звуковые волны в воздухе.
Волновые процессы и колебания разной природы имеют много общего, а их распространение может быть описано аналогичными математическими уравнениями. Это подтверждает единство материального мира.
Гармонические колебания. Определение
В механике предусмотрено движение поступательно, вращательно и с наличием колебаний.
Механические колебания – это движения тел, которые повторяются точно или приблизительно за определенные одинаковые временные промежутки.
Функция x = f ( t ) объясняет закон движения тела с наличием колебаний. При графическом изображении дается представление о протекании колебательного процесса во времени. Рисунок 2 . 1 . 1 наглядно показывает принцип простых колебательных систем груза на пружине или математического маятника.
Рисунок 2 . 1 . 1 . Механические колебательные системы.
Механические колебания подразделяют на свободные и вынужденные.
Действия внутренних сил системы после выведения из равновесия порождают свободные колебания. Примером могут служить колебания груза на пружине или маятника. Если их действие происходит под воздействием внешних сил, тогда их называют вынужденными.
Простейшим видом колебаний являются гармонические колебания, которые описываются уравнением x = x m cos ( ω t + φ 0 ) , где x – смещение тела от положения равновесия, x m – амплитуда колебаний, ω – циклическая или круговая частота, t – время.
Величина, располагаемая под знаком косинуса, получила название фазы гармонического процесса: φ = ω t + φ 0 . Если t = 0 , φ = φ 0 , тогда φ 0 рассматривается в качестве начальной фазы.
Период колебаний Т – это минимальный промежуток времени, через который происходят повторения движения тела. Величина, обратная периоду колебаний, называют частотой колебаний f = 1 T .
Частота гармонических колебаний показывает их количество, совершаемое за единицу времени, измеряемая в герцах ( Г ) . Связь с циклической частотой ω и периодом T выражается с помощью формулы:
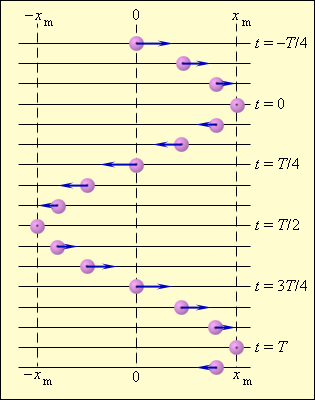
Рисунок 2 . 1 . 2 показывает гармонические колебания тел с разными положениями тел. Данный эксперимент наблюдается в специальных условиях при наличии периодических вспышек освещения, называемого стробоскопическим. Для изображения векторов скорости тела в разные моменты времени используют стрелки.
Рисунок 2 . 1 . 2 . Стробоскопическое изображение гармонических колебаний. Начальная фаза φ 0 = 0 . Интервал времени между последовательными положениями тела τ = T 12 .
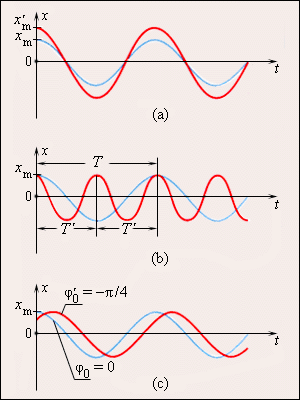
На графике 2 . 1 . 3 . показаны изменения, происходящие во время гармонического процесса, при изменении амплитуды колебаний x m , или периода Т (частоты f ), или начальной фазы φ 0 .
Рисунок 2 . 1 . 3 . Во всех трех случаях для синих кривых φ 0 = 0 : a – красная кривая отличается от синей только большей амплитудой ( x ‘ m > x m ) ; b – красная кривая отличается от синей только значением периода ( T ‘ = T 2 ) ; с – красная кривая отличается от синей только значением начальной фазы φ 0 ‘ = — π 2 р а д .
Гармонический закон
Если колебания совершаются вдоль прямой О х , тогда направление вектора скорости аналогично. Определение скорости движения тела υ = υ x определяют из выражения υ = ∆ x ∆ t ; ∆ t → 0 .
Отношение ∆ x ∆ t при ∆ t → 0 математика трактует как вычисление производной функции x ( t ) за определенное время t . Обозначение принимает вид d x ( t ) d t , x ‘ ( t ) или x ˙ .
Гармонический закон движения записывается в качестве x = x m cos ( ω t + φ 0 ) . После вычисления производной формула приобретает вид:
υ = x ˙ ( t ) = — ω x m sin ( ω t + φ 0 ) = ω x m cos ω t + φ 0 + π 2 .
Слагаемое + π 2 считают изменением начальной фазы. Достижение максимального значения скорости по модулю υ = ω x m производится при прохождении тела через положение равновесия, то есть x = 0 . Аналогично определяют ускорение a = a x . Тогда a = ∆ υ ∆ t , ∆ t → 0 . Отсюда следует, что a равняется производной функции υ ( t ) за время t или второй производной функции x ( t ) . Подставив выражения, получим
a = υ ˙ ( t ) = x ¨ ( t ) = — ω 2 x m cos ( ω t + φ 0 ) = — ω 2 x ( t ) .
Наличие отрицательного знака указывает на то, что ускорение a ( t ) имеет противоположный смещению x ( t ) знак. Исходя из второго закона Ньютона, сила, которая заставляет совершать колебательные движения, направляется в сторону положения равновесия x = 0 .
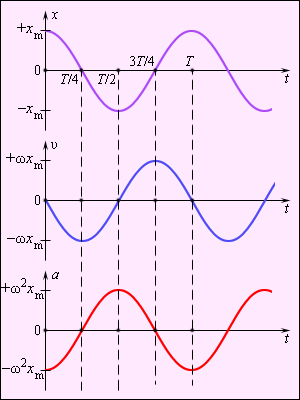
На рисунке 2 . 1 . 4 изображены графики, где имеются зависимости скорости, ускорения, совершающие гармонические колебания.
Рисунок 2 . 1 . 4 . Графики координаты x ( t ) , скорости υ ( t ) и ускорения a ( t ) тела, совершающего гармонические колебания.
Рисунок 2 . 1 . 5 . Модель гармонических колебаний.
Источник статьи: http://zaochnik.com/spravochnik/fizika/mehanicheskie-kolebanija/garmonicheskie-kolebanija/
Гармонические колебания
Колебательное движение – движение (изменение состояния), обладающее той или иной степенью повторяемости во времени.
Т.е. колебанием можно назвать любой вид движения, при котором через одинаковые промежутки времени повторяются кинематические характеристики движения (координата, скорость, ускорение).
Гармоническими колебаниями называются колебания, кинематические характеристики в которых меняются по закону синуса или косинуса.
Рис. 1. Колебательное движение. Вывод через окружность. Начальные условия
Для визуализации, представим вращательное движение в виде колебательного движения вдоль двух взаимно перпендикулярных осей.
Пусть тело, вращающееся по окружности радиуса A, в начале движения находилось в точке C. Пусть в начале движения радиус-вектор, описывающий выбранную точку, наклонён под углом к оси OX. Определим начальные координаты тела (исходя из проекций радиуса на оси):
Рис. 2. Колебательное движение. Вывод через окружность
Пусть через время тело, вращаясь с угловой скоростью , переместилось в точку D. При этом угол поворота радиус-вектора, относительно начального положения составил (рис. 2).
Определим текущие координаты тела тем же методом:
Учитывая, что при равномерном движении по окружности , получим:
Уравнения (5) и (6) являются законом движения материальной точки при гармонических колебаниях. Причём, одним и тем же законом, так как с тригонометрической точки зрения , тогда из (5):
- где — новый параметр, характеризующий некое другое начальное положение тела.
Таким образом, уравнения (5) и (6), по сути, являются одинаковыми уравнениями только при разных начальных условиях.
Разберём уравнение (5). Каждый из введённых параметров, имея аналог во вращательном движении, описывается по-другому в колебательном движении:
- где
- — текущая координата тела,
- — амплитуда колебаний (максимальное отклонение тела от положения равновесия)
- — циклическая частота колебания
- — время движения
- — начальная фаза колебания
- — текущая фаза колебания (всё, что стоит под тригонометрической функцией).
Зная общий вид колебательного движения, можем найти зависимости скорости и ускорения от времени. Для уравнения (5):
Аналогичным образом можно провести рассмотрение уравнения (6).
Проанализируем (5) и (8), исходя из внешнего вида правой части обоих уравнений, можем вывести:
Уравнение (9) называется основным уравнением гармонических колебаний.
Среди параметров колебаний также присутствуют параметры, знакомые нам по вращательному движению:
- где
- — циклическая частота колебаний
- — период колебаний
- — частота колебания.
Вывод: для школьных задач почти все колебания являются гармоническими и описываются соотношениями (5), (6). Соответствующие скорость и ускорение частицы рассчитываются исходя из конкретного колебания. Параметры колебания также рассчитываются формульно.
Источник статьи: http://www.abitur.by/fizika/teoreticheskie-osnovy-fiziki/garmonicheskie-kolebaniya/
Построение графиков гармонических колебаний
Международные дистанционные “ШКОЛЬНЫЕ ИНФОКОНКУРСЫ”
для дошкольников и учеников 1–11 классов
МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Югорский государственный университет» (ЮГУ)
НИЖНЕВАРТОВСКИЙ НЕФТЯНОЙ ТЕХНИКУМ
(филиал) федерального государственного бюджетного образовательного учреждения
высшего профессионального образования «Югорский государственный университет»
На заседании кафедры ЕиЭД
Зам. директора по учебной работе
ННТ (филиала) ФГБОУ ВПО «ЮГУ»
Методическая разработка занятия
« Построение графиков гармонических колебаний »
Преподаватель: Е.Н. Карсакова
«Построение графиков гармонических колебаний »
Формирование навыков построения графиков гармонических колебаний;
Закрепление умений преобразования графиков функций;
Применение знаний к решению нестандартных задач по смежным дисциплинам;
Способствовать развитию алгоритмического и логического мышления;
Развитие точной, информативной речи;
Формирование навыков исследовательской работы;
Развитие творчества, инициативности;
Способствовать эстетическому восприятию графических изображений;
Воспитание умений действовать по заданному алгоритму;
Воспитание аккуратного, точного выполнения геометрических построений;
Тип занятия: формирование умений и навыков
Оборудование и материалы: МД проектор, карты с заданиями, тетради, линейки, карандаши.
Н.В. Богомолов « Практические занятия по математике», 2006г.
А.А. Дадаян « Математика», 2003г.
О.Н. Афанасьева, Я.С. Бродский « Математика для техникумов», 2001г
Объявление темы занятия; постановка целей;
Мотивация познавательной деятельности
Повторить виды преобразований графиков функций и алгоритмы их выполнения; коррекция пробелов в знаниях
изучению нового материала
Формирование умений и навыков построения графиков.
Построение графиков гармонических колебаний.
Закрепление умений и навыков построения графиков функций
Демонстрация лучших работ студентов.
Воспитание эстетического восприятия графических изображений;
Применение знаний к решению нестандартных задач
Показать связь математики с другими науками
Обобщение знаний, умений, навыков; оценка деятельности студентов
Инструктаж по домашнему заданию
Рождённый пустыней, колеблется звук,
Колеблется синий на нитке паук.
Колеблется воздух, прозрачен и чист,
В сияющих звездах колеблется лист.
Сообщение темы занятия; постановка целей; освещение основных этапов.
В технике и в окружающем нас мире часто приходится сталкиваться с периодическими процессами, которые повторяются через одинаковые промежутки времени. Такие процессы называют колебательными . Колебательные явления различной физической природы подчиняются общим закономерностям. Например, колебания тока в электрической цепи и колебания математического маятника могут описываться одинаковыми уравнениями. Общность колебательных закономерностей позволяет рассматривать все колебательные процессы с единой точки зрения.
Механическими колебаниями называются периодические изменения физической величины, описывающей механическое движение (скорость, перемещение, кинетическая и потенциальная энергия и т. п.).
Если в какой-либо точке среды, в которой близко расположенные атомы или молекулы испытывают силовое воздействие, возбужден процесс механических колебаний, то этот процесс будет с конечной скоростью, зависящей от свойств среды, распространяться от точки к точке. Так возникают механические волны . Примерами такого процесса являются звуковые волны в воздухе.
Как и колебания, волновые процессы различной физической природы (звук, электромагнитные волны, волны на поверхности жидкости и т. д.) имеют много общего. Распространение волн различной физической природы можно описывать с помощью одинаковых математических уравнений и функций. В этом проявляется единство материального мира.
Цель: Мотивация познавательной деятельности
Сегодня мы увидим, как с помощью математических законов и преобразований можно описывать некоторые физические явления. Например,
Что такое гармонические колебания?
Гармонические колебания – это периодические изменения физической величины в зависимости от времени, происходящие по закону синуса или косинуса. Графиком гармонического колебания является синусоида или косинусоида , по которой можно определить все характеристики колебательного движения : амплитуду, период, частоту, начальную фазу .
Гармонические колебания играют важную роль в физике, электротехнике. Наша задача – построить графики гармонических колебаний, применив при этом все известные правила преобразований графиков без помощи трудоёмких вычислений и научиться описывать по ним колебательный процесс.
Гармонические колебания подчиняются следующему закону:
А — амплитуда, 
циклическая (круговая) частота,
начальная фаза колебаний, обычно 
Период гармонических колебаний Т можно вычислить по формуле 
Для построения графиков гармонических колебаний необходимо иметь чёткое представление о правилах построения графиков функций и их преобразованиях.
3. Проверка знаний учащихся по теме: «Преобразования графиков функций» (15 мин.)
Цель: Повторить основные виды преобразований графиков функций и алгоритмы их выполнения; коррекция пробелов в знаниях.
Задание 1. Сгруппируйте функции по общему признаку:
Рассмотрим подробно правила построения графиков функций с изменяющимся аргументом и меняющейся функцией. (Презентация.)
4. Изучение нового материала (20 мин.) (Презентация.)
Цель: Формирование умений и навыков исследования функции, построения графиков гармонических колебаний.
Задача 1. Построить график гармонических колебаний у = 2 sin (2 x — 
).
Сразу укажем на типовую ошибку в подобных задачах: осуществляют сдвиг на , а необходимо на 
, поэтому у = 2 sin 2( x — ).
Как построить график такого колебания? Алгоритм построения следующий:
1. у = sinx — исходная функция .
2. у = sin 2 x — сжатие в 2 раза вдоль оси Ох.
3. у = 2 sin 2 x — растяжение в 2 раза вдоль оси Оу (рис. 1).
4. у = 2 sin 2( x — ) — сдвиг на вправо по оси Оx (рис. 2).
При построении данного графика были использованы следующие виды преобразования графиков:
Задача 2. Построить графики функций и определить основные характеристики гармонического колебания:
a ) у = sin 
б) у = sin 3 x
a). Найдем период функции у = sin :
А=1; 
Период колебания Т = 6 
значит, достаточно построить график на участке 
. Поделив этот участок на 4 равных промежутка, получим точки, которые определяют поведение графика: 
(рис. 3).
А=1; 
Построим график на участке длиной в период 
. Поделим его на 4 равных промежутка и получим точки 
(рис. 4).
5. Построение графиков гармонических колебаний . Самостоятельная работа (30 мин).
Опыт – дитя мысли, мысль – дитя действий
Цель: Закрепление умений и навыков построения графиков функций
Построить графики гармонических колебаний:
y = cos
y = — sin ( x+ ).
Критерии оценки деятельности учащихся:
(1-) – удовлетворительно; (1-2) – хорошо; (1-3) – отлично.
6. Демонстрация лучших работ студентов (3 мин).
Вдохновение нужно в математике, как и в поэзии.
Цель: Воспитание эстетического восприятия графических изображений;
7. Применение знаний к решению нестандартных задач (6 мин.)
Цель: Показать связь математики с другими науками;
Тело движется по закону у = cos 
. По графику (рис.5)функции установите:
Частоту колебаний 
Период колебаний 
;
Начальную фазу 
Ответ : А=1; 
Дорогу осилит идущий, а математику – мыслящий.
Выполнение поставленных целей;
Приобретение навыков исследовательской работы;
Применение знаний к решению нестандартных задач;
Мы познакомились с графиками гармонических колебаний. Очевидно, что при их построении синусоида или косинусоида подверглись различным преобразованиям: сжатию, растяжению, сдвигу. Овладение этими правилами поможет при изучении других функций на последующих занятиях.
Построить график функции у = 3 cos (2 x + 
) и определить основные характеристики колебательного движения.
Биение сердца также относится к колебательному процессу. В течение минуты оно выбрасывает в аорту около 4 л крови. Сердце человека в среднем сокращается 100 тысяч раз в сутки. За 70 лет жизни оно сокращается 2 миллиарда 600 миллионов раз и перекачивает при этом 250 миллионов литров крови. Синусоидальные изменения ритмов сердца отражает кардиограф.
Источник статьи: http://infourok.ru/postroenie-grafikov-garmonicheskih-kolebaniy-776798.html