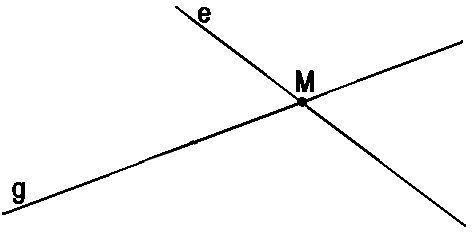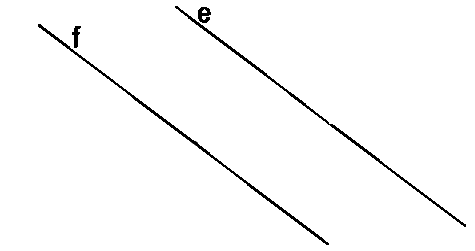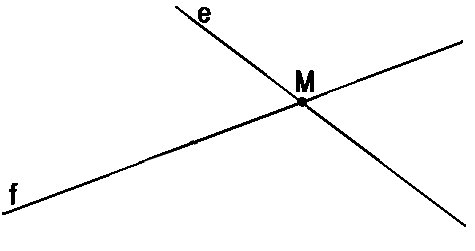Урок 31. Проверка принадлежности точки отрезку
Урок из серии «Геометрические алгоритмы»
Здравствуйте, дорогой читатель!
Сегодня мы рассмотрим еще одну типовую задачу из серии геометрические алгоритмы. Напишем функцию, которая будет проверять принадлежность произвольной точки отрезку, заданному координатами своего начала и конца.
Для реализации операций сравнения над вещественными данными напишем еще две функции: функцию EqPoint(), которая ,будет проверять, совпадают ли две точки на плоскости и функцию RealMoreEq() , которую будем использовать для проверки отношения «>=» (больше или равно). Причина ввода специальных функций нам уже известна.
Задача. Проверить, принадлежит ли точка отрезку.
Пусть точки 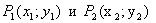
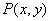
Вектор с началом в точке 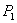
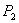
Если P(x, y) – произвольная точка, то координаты вектора 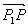
Точка Р будет принадлежать отрезку если:
- Векторы в
и
коллинеарны (равно нулю их векторное произведение):
, т.е. (x-x1)(y2-y1)-(y-y1)(x2-x1) = 0
- Абсцисса точки P удовлетворяет условию:
или
. Иначе точка будет находиться на прямой левее или правее отрезка.
Результаты выполнения программы.
Введите координаты точек: x1, y1, x2, y2, x,y
0.5 1 2.5 2.8 1.203 1.633
Да.
Результаты тестирования в программе GeoGebra:
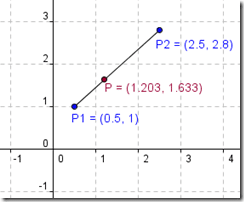
Сегодня мы написали функцию AtOtres() , которая проверяет принадлежность произвольной точки отрезку, заданному своими координатами.
Ввели еще две функции: EqPoint() и RealMoreEq() для реализации операций сравнения над вещественными данными. Первая проверяет, совпадают ли две точки на плоскости, вторая — используется для проверки отношения «>=».
На следующем уроке, на основе ранее написанных процедур, напишем процедуру определения координат точки пересечения двух отрезков.
На этом я с вами прощаюсь. До встречи на следующем уроке.
Источник статьи: http://gospodaretsva.com/urok-31-proverka-prinadlezhnosti-tochki-otrezku.html
Как определить принадлежит ли точка отрезку или нет?
Форумы CADUser → Программирование → LISP → Как определить принадлежит ли точка отрезку или нет?
Чтобы отправить ответ, вы должны войти или зарегистрироваться
Сообщения 15
#1 Тема от Олег 15 июня 2004г. 11:15:36
- Олег
- Восстановленный участник
- На форуме с 21 мая 2004г.
- Сообщений: 9
- Спасибо: 0
Тема: Как определить принадлежит ли точка отрезку или нет?
Как определить принадлежит ли точка отрезку или нет?
#2 Ответ от VH 15 июня 2004г. 11:19:04
- VH
- Активный участник
- На форуме с 14 июня 2001г.
- Сообщений: 1,381
- Спасибо: 7
Re: Как определить принадлежит ли точка отрезку или нет?
Точка принадлежит отрезку, если сумма расстояний от этой точки до конечных точек отрезка равна длине отрезка.
#3 Ответ от AY 15 июня 2004г. 16:13:10
- AY
- Восстановленный участник
- На форуме с 22 августа 2003г.
- Сообщений: 465
- Спасибо: 0
Re: Как определить принадлежит ли точка отрезку или нет?
Очень интерестно проходит ли такая проверка.
Я в свое время для похожей задачи по двум точкам отрезка задавал уравнение прямой и подставлял в него координаты точки. Теоретически если точка на прямой уравнение обнуляется (aX+bY+c=0) на практике условие проходило если отрезок горизонтален или вертикален (точку получал указанием с привязкой к ближнему), ели нет погрешность приходилось учитывать (при конечной точности вычислений в данном случае это неизбежно) .
#4 Ответ от Alexander 15 июня 2004г. 19:48:21
- Alexander
- Восстановленный участник
- На форуме с 1 июня 2004г.
- Сообщений: 42
- Спасибо: 0
Re: Как определить принадлежит ли точка отрезку или нет?
Если устроит попробуйте использовать
функцию (vlax-curve-getParamatPoint ).
Если вернёт nil значит точка не лежит на кривой.
У Полещука написано — VLA-объект,
но как показывает практика можно и имя примитива.
#5 Ответ от kserg 15 июня 2004г. 21:25:20
- kserg
- Активный участник
- На форуме с 2 апреля 2004г.
- Сообщений: 260
- Спасибо: 0
Re: Как определить принадлежит ли точка отрезку или нет?
Когда-то (в AutoCAD10) выходил из положения так :
(setq Nabor (ssget «_C» t1 t1))
,- где t1 — координаты точки [например, ‘(150 175 0)],
а затем, перебирал объекты, попавшие в набор «Nabor», на предмет наличия среди них того самого отрезка.
#6 Ответ от Leonid 15 июня 2004г. 22:08:57
- Leonid
- Восстановленный участник
- На форуме с 16 июня 2003г.
- Сообщений: 389
- Спасибо: 0
Re: Как определить принадлежит ли точка отрезку или нет?
Я в свое время точно также как и AY пытался решить эту задачу на основе линейных уравнений. Оказалось, что камнем преткновения является погрешность вычислений. В итоге, метод работает ненадежно и неустойчиво. По-видимому, сама постановка вопроса -Точка принадлежит линии — при переводе в практическую плоскость нуждается в переосмыслении. А что есть прямая (линия), ведь это не более чем выдумка античных математиков. ведь она не имеет толщины, и следовательно — не существует. Я понимаю, все это звучит несколько академически, однако вопрос надо решать!
Давайте считать линией полосу конечной ширины, и при постановке задачи указывать эту ширину. Интересно было бы услышать мнение профессиональных математиков, например, специалистов по теории множеств.
#7 Ответ от Fantomas 16 июня 2004г. 01:28:17
- Fantomas
- Восстановленный участник
- На форуме с 7 декабря 2003г.
- Сообщений: 392
- Спасибо: 0
Re: Как определить принадлежит ли точка отрезку или нет?
Тоже недавно делал проверку принадлежности точки сфере. Естественно сравнение через EQUAL, смотря какая точность нужна.
Есть еще идея. Существует функция vlax-curve-getDistAtPoint которая вычисляет расстояние между начальной точкой кривой (а в нашем случае отрезка) до точки на кривой. В случае если точка не лежит на кривой она возвратит Nil.
Источник статьи: http://www.caduser.ru/forum/topic10577.html
Геометрия 7 класс.
Точка, прямая и отрезок
Казалось бы, что таким простым понятиям, как «точка» или «прямая», которые мы повседневно используем в жизни, крайне просто дать определения. Но на практике оказалось, что это не так.
Существует множество определений, которые давали знаменитые математики терминам «точка» и «прямая». За многие века ученые так и не пришли к единому определению.
Мы не будем приводить все определения точки и прямой. Остановимся на объяснениях, которые, на наш взгляд, наиболее простым образом их описывают.
Точка — элементарная фигура, не имеющая частей.
Прямая состоит из множества точек и простирается бесконечно в обе стороны.
На рисунке изображена прямая a и точки D, F, G и H . Точки F и G лежат на прямой a . Точки D и H не лежат на прямой a .
В тексте точку обозначают символом « (·)» . Принадлежность и непринадлежность точки прямой обозначают символами « ∈ » и « ∉ ». Знак принадлежности можно запомнить как зеркальное отображение буквы « Э » или как знак евро « € » .
То есть выражаясь геометрическими обозначениями, информацию о расположении прямой и точек на рисунке выше можно записать так:
- (·)F ∈ a — точка F принадлежит прямой a (другими словами, точка F лежит на прямой a );
- (·)G ∈ a — точка G принадлежит прямой a ;
- (·)D ∉ a — точка D не принадлежит прямой a (другими словами, точка D не лежит на прямой a );
- (·)H ∉ a — точка H не принадлежит прямой a .
Как обозначить прямую
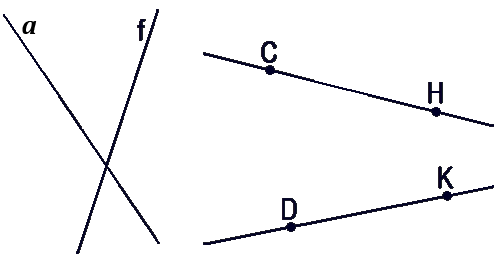
Прямую обычно обозначают одной маленькой латинской буквой.
Прямую, на которой отмечены две точки, иногда обозначают по названиям этих точек большими латинскими точками.
- На рисунке изображены:
- Прямая a
- Прямая f
- Прямая CH
- Прямая DK
Точки D, E и F — лежат на одной прямой, поэтому: прямая DE , прямая EF и прямая DF — это три разных имени одной и той же прямой.
Задача № 1 из учебника Атанасян 7-9 класс
Проведите прямую, обозначьте её буквой a и отметьте точки A и B , лежащие на этой прямой, и точки P, Q и R , не лежащие на ней. Опишите взаимное расположение точек A, B, P, Q, R и прямой a , используя символы ∈ и ∉ .
Решение задачи
Отметим точки (·)A и (·)B , лежащие на прямой a .
Отметим точки (·)P, (·)Q и (·)R , не лежащие на прямой a .
Опишем взаимное расположение точек и прямой.
Как обозначается пересечение прямых
На рисунке прямые a и b не пересекаются . Прямые b и c пересекаются .
Хотя на чертеже не видно, но прямые a и c тоже пересекаются (это становится ясно, если мысленно продолжить вниз прямые a и с ).
В тексте пересечение прямых обозначают символом ∩ . Информацию на рисунке выше можно записать следующим образом:
- b ∩ c — прямые b и с пересекаются;
- a ∩ c — прямые a и с пересекаются.
Прямые e и g имеют общую точку M . Другими словами, прямые пересекаются в точке M . Геометрическими обозначениями пересечение прямых в точке записывается так:
e ∩ g = (·)M
Прямые e и f не имеют общей точки — т.е. они не пересекаются.
Взаимное расположение прямой и точек
Через любые две точки можно провести прямую, и притом только одну .
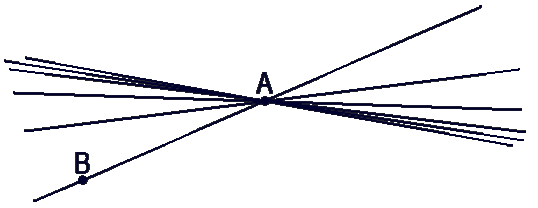
Через одну точку (·)A можно провести сколько угодно прямых.
Через две точки (·)A и (·)B можно провести только одну прямую.
Сколько общих точек имеют две прямые
Две прямые либо имеют только одну общую точку, либо не имеют общих точек.
Докажем утверждение выше. Для этого рассмотрим все возможные случаи расположения двух прямых.
Первый случай расположения прямых
На рисунке выше мы видим, что у прямых f и e нет общих точек, т.к. эти прямые не пересекаются.
Второй случай расположения прямых
Возможен вариант, что прямые f и e пересекаются и, значит, имеют одну общую точку (·)M .
Третий случай расположения прямых
Предположим, что прямые f и e имеют две или больше общих точек. Например, точки (·)A и (·)B .
Но мы знаем, что через две точки можно провести только одну прямую. Значит, прямые f и e совпадают и наше предположение, что у двух прямых может быть две или более общих точек неверно .
Вывод: две прямые либо имеют только одну общую точку, либо не имеют общих точек.
Задача № 3 из учебника Атанасян 7-9 класс
Проведите три прямые так, чтобы каждые две из них пересекались. Обозначьте все точки пересечения этих прямых. Сколько получилось точек? Рассмотрите все возможные случаи.
Решение задачи
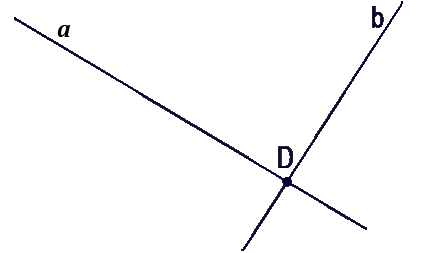
Проведём две прямые a и b так, чтобы эти две прямые пересекались, и обозначим точку пересечения.
Как мы видим, точка пересечения только одна. Мы можем провести третью прямую так, чтобы она тоже проходила через эту точку пересечения.
Теперь прямая a пересекается с прямой b , прямая b пересекается с прямой c и прямая c пересекается с прямой a .
В этом случае у нас только одна точка пересечения всех прямых — точка (·)D .
Но возможен и другой вариант. Мы можем провести третью прямую c так, чтобы она не проходила через точку (·)D . Тогда получится три точки пересечения — (·)D, (·)E и (·)F .
Прямая a пересекается с прямой b в точке (·)D , прямая b пересекается с прямой c в точке (·)F и прямая c пересекается с прямой a в точке (·)E . Условие задачи выполнено.
Мы убедились, что возможны оба варианта. Поэтому в ответе запишем их оба.
Ответ: точек пересечения получается одна или три.
Что такое отрезок
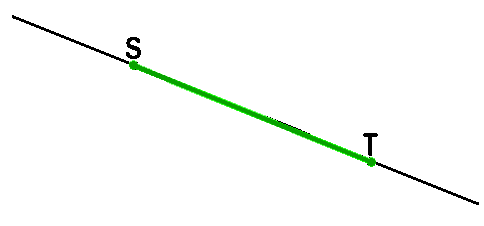
Отрезок — часть прямой, ограниченная двумя точками.
Две точки, ограничивающие отрезок, называются концами отрезка. У отрезка на рисунке выше концы называются S и T .
Сам отрезок можно назвать ST или TS . Когда изображают отрезок, оставшиеся от прямой хвосты можно не рисовать.
В отличии от прямой любой отрезок можно измерить. Т.е. каждый отрезок имеет длину.
Источник статьи: http://math-prosto.ru/?page=pages/point_straight_segment/point_straight_segment_geometry_7_grade.php&showArrow=1

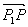 и
и 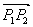 коллинеарны (равно нулю их векторное произведение):
коллинеарны (равно нулю их векторное произведение): 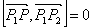 , т.е. (x-x1)(y2-y1)-(y-y1)(x2-x1) = 0
, т.е. (x-x1)(y2-y1)-(y-y1)(x2-x1) = 0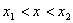 или
или 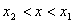 . Иначе точка будет находиться на прямой левее или правее отрезка.
. Иначе точка будет находиться на прямой левее или правее отрезка.