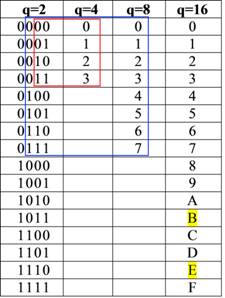
Развернутая форма записи числа



В позиционной системе счисления число можно представить в развернутой форме (в виде суммы разрядных слагаемых) и в свернутой форме. Именно такой формой записи чисел мы и пользуемся в повседневной жизни. Иначе свернутую форму записи называют естественной или цифровой.
Десятичное число А10= 4718,63 в развернутой форме будет имеет вид:
А10 = 4718,6310 = 4*10 3 + 7*10 2 + 1*10 1 + 8*10 0 + 6*10 -1 + 3*10 -2 .
Рассмотрим еще примеры записи чисел в развернутом виде
58910 → 500 + 80 + 9 = 5*100 + 8*10 + 9*1 = 5*10 2 +8*10 1 + 9*10 0
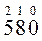
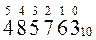
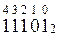
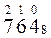
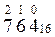
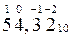
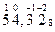
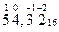
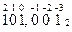
Задания для самостоятельной работы
Задание 1. Запишите числа в развернутой форме
| 1) | 11110102 | 6) | 111101,0012 | 11) | 1110,112 | 16) | 100011102 |
| 2) | 2174,55 | 7) | 5771,0015 | 12) | 89784515 | 17) | 514763175 |
| 3) | 6479118 | 8) | 1622,848 | 13) | 1114878 | 18) | 113874,3348 |
| 4) | 1214710 | 9) | 512001410 | 14) | 1874,59610 | 19) | 1554,01410 |
| 5) | 1247,032116 | 10) | 15789416 | 15) | 163201,9816 | 20) | 88541216 |
Перевод чисел в десятичную систему счисления
1. Записать число в развернутом виде
2. Выполнить вычисления как в десятичной системе счисления
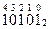
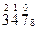
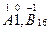
Источник статьи: http://studopedia.ru/12_126318_razvernutaya-forma-zapisi-chisla.html
Развернутая форма записи числа
СИСТЕМЫ СЧИСЛЕНИЯ И
ПЕРЕВОД ЧИСЕЛ ИЗ ОДНОЙ СИСТЕМЫ В ДРУГУЮ
Система счисления (СС)- это способ представления чисел и соответствующие ему правила действий над ними.
Системы счисления делятся на позиционные и непозиционные
| Название | Позиционные | Непозиционные |
| Определение | Значение цифры в записи числа зависит от её позиции | От положения знака в изображении числа не зависит величина которую он обозначает |
| Пример | Арабская десятичная  | Римская ССXXII |
| Алфавит | 0 1 2 3 4 5 6 7 8 9 |  |
| Основание | 10 | 7 |
Основанием системы счисления — называют количество цифр используемых для записи чисел
Алфавитом СС — называют все цифры (знаки) используемые для записи чисел
Развернутая форма записи числа
n — количество разрядов целой части
m — количество разрядов дробной части
123,4510=100+20+3+0,4+0,05=1∙10 2 +2∙10 1 +3∙10 0 +4∙10 -1 +5∙10 -2
123,458=1∙8 2 +2∙8 1 +3∙8 0 +4∙8 -1 +5∙8 -2
Таблица эквивалентов чисел
| q=10 | q=16 | q=12 | q=8 | q=5 | q=4 | q=2 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 2 | 2 | 2 | 2 | 2 | 10 |
| 3 | 3 | 3 | 3 | 3 | 3 | 11 |
| 4 | 4 | 4 | 4 | 4 | 10 | 100 |
| 5 | 5 | 5 | 5 | 10 | 11 | 101 |
| 6 | 6 | 6 | 6 | 11 | 12 | 110 |
| 7 | 7 | 7 | 7 | 12 | 13 | 111 |
| 8 | 8 | 8 | 10 | 13 | 20 | 1000 |
| 9 | 9 | 9 | 11 | 14 | 21 | 1001 |
| 10 | А | А | 12 | 20 | 22 | 1010 |
| 11 | В | В | 13 | 21 | 23 | 1011 |
| 12 | С | 10 | 14 | 22 | 30 | 1100 |
| 13 | D | 11 | 15 | 23 | 31 | 1101 |
| 14 | E | 12 | 16 | 24 | 32 | 1110 |
| 15 | F | 13 | 17 | 30 | 33 | 1111 |
| 16 | 10 | 14 | 20 | 31 | 100 | 10000 |
Полужирным шрифтом выделены алфавиты в соответствующих системах счисления.
Правило перевода числа из любой системы счисления в десятичную
Чтобы перевести число в десятичную систему счисления надо:
1. записать число в развернутой форме
2. все цифры перевести в десятичную СС (для СС с q>10)
3. вычислить значение полученного выражения
123,458=1∙8 2 +2∙8 1 +3∙8 0 +4∙8 -1 +5∙8 -2 =64+16+3+0,5+5/64=83,57810
1BE,8416=1∙16 2 +B∙16 1 +E∙16 0 +8∙16 -1 +4∙16 -2 =
=1∙16 2 +11∙16 1 +14∙16 0 +8∙16 -1 +4∙16 -2 =
Решите примеры:
Правило перевода целых десятичных чисел в другие системы счисления:
1. Последовательно выполнять деление с остатком данного числа и получаемых неполных частных на основание новой СС до тех пор пока не получим неполное частное, меньшее делителя.
2. Полученные остатки, являющиеся цифрами числа в новой СС, привести в соответствие с алфавитом новой СС (для СС с q>10)
3. Составить число в новой СС, записывая все остатки, начиная с последнего частного
| 1910 = 100112 |  |
| 1910 = 1316 |  |
| 20510 = CD16 |  |
Решите примеры:
Быстрый Перевод в двоичную систему счисления разложением на степени двойки
Перевод числа в двоичную СС для некоторых чисел удобно производить вторым способом: разложением на степени двойки. Конечно, для этого эти степени надо знать наизусть 😉
1910 = 16 + 2 + 1 = 2 4 + 2 1 + 2 0 =1∙2 4 + 0∙2 3 +0∙2 2 +1∙2 1 + 1∙2 0 =100112
Можно пропустить развернутую форму записи числа. Если степень есть, то ставим единицу, если по порядку степени нет (в нашем примере 3 и 2), то там ставим 0.
1910 = 16 + 2 + 1 = 2 4 + 2 1 + 2 0 = 100112
Особенно удобен этот способ для чисел значение которых близко к степени.
Решите примеры:
Правило перевода двоичного числа в СС с основанием q=2 n
1. данное двоичное число разбить начиная от запятой (целую и дробную части) на группы по n цифр в каждой
2. если в последних (крайних) группах окажется менее n разрядов, то их надо дополнить (с краю) незначащими нулями до нужного числа разрядов.
3. заменить каждую n-разрядную группу цифр соответствующей цифрой в СС основанием q=2 n
Для перевода необходимо пользоваться таблицей эквивалентов чисел.
Решите примеры:
Правило перевода чисел в СС с основанием q=2 n в двоичную СС
Чтобы число из СС с основанием q=2 n перевести в двоичную СС, надо каждую цифру этого числа заменить её n-разрядным эквивалентом в двоичной СС.
Источник статьи: http://lektsii.org/17-72934.html
Развернутая и свернутая формы записи чисел



Основанием позиционной системы счисления называется целое число q, которое возводится в степень.
Базисом позиционной системы счисления называется последовательность чисел, каждое из которых определяет количественный эквивалент (вес) символа в зависимости от его места в коде числа.
Базис десятичной системы счисления: …10 n , 10 n –1 ,…, 10 1 , 10 0 , 10 –1 , …, 10 – m ,…
Базис произвольной позиционной системы счисления: …q n , q n –1 , …, q 1 , q 0 , q –1 , …, q – m , …
Основание в любой системе изображается как 10, но имеет разное количественное значение. Оно показывает, во сколько раз изменяется количественное значение цифры при перемещении ее на соседнюю позицию. Возможно множество позиционных систем, так как за основание системы счисления можно принять любое число, не меньшее 2.
Наименование системы счисления соответствует ее основанию (десятичная, двоичная, пятеричная и т. д.).
В системе счисления с основанием q (q-ичная система счисления) единицами разрядов служат последовательные степени числа q, иначе говоря, q единиц какого-либо разряда образуют единицу следующего разряда.
Для записи чисел в q-ичной системе счисления требуется q различных знаков (цифр), изображающих числа 0, 1, . q – 1.
Следовательно, основание позиционной системы счисления равно количеству символов (знаков) в ее алфавите. Запись числа q в q-ичной системе счисления имеет вид 10.
Пример 1.Восьмеричная система счисления.
Алфавит: 0, 1, 2, 3, 4, 5, 6 и 7.
Числа: например, 45023,1528; 751,0018.
Пример 2.Пятеричная система счисления.
Пример 3.Шестнадцатеричная система счисления.
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, E, F.
Здесь только десять цифр из шестнадцати имеют общепринятое обозначение 0—9. Для записи остальных символов алфавита (10, 11, 12, 13, 14 и 15) обычно используются первые пять букв латинского алфавита.
Числа: например, В5С3,1А216; 355,0FА018.
В позиционной системе счисления любое вещественное число может быть представлено в следующем виде:
Aq = ±(an–1×q n –1 + an–2×q n –2 +…+ a0×q 0 + a–1×q –1 + a–2×q –2 +…+ a–m×q –m ), (1) или 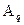
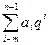
Здесь А — само число; q — основание системы счисления;
аi — цифры, принадлежащие алфавиту данной системы счисления; п — количество целых разрядов числа; т — количество дробных разрядов числа.
Разложение числа по формуле (1) называется развернутой формой записи. Иначе такую форму записи называют многочленной или степенной.
Пример 1.Десятичное число А10 = 5867,91 по формуле (1) представляется следующим образом:
A10 = 5×10 3 + 8 × 10 2 + 6 × 10 1 + 7 × 10 0 + 9 × 10 –1 + 1 × 10 –2 .
Пример 2.Формула (1) для восьмеричной системы счисления имеет вид:
Восьмеричное число A8 = 7064,3 в виде (1) запишется так:
A8 = 7 × 8 3 + 0 × 8 2 + 6 × 8 1 + 4 × 8 0 + 3 × 8 –1 .
Пример 3.Пятеричное число А5 = 2430,21 по формуле (1) запишется так:
А5 = 2 × 5 3 + 4 × 5 2 + 3 × 5′ + 0 × 5° + 2 × 5 –1 + 1 × 5 –2 .
Вычислив это выражение, можно получить десятичный эквивалент указанного пятеричного числа: 365,4410.
Пример 4.В шестнадцатеричной системе счисления запись 3AF16 означает:
3AF16 = 3 × 16 2 + 10 × 16 1 + 15 × 16 0 = 768 + 160 + 15 = 94310.
Источник статьи: http://studopedia.ru/3_53822_razvernutaya-i-svernutaya-formi-zapisi-chisel.html