Факториал в «Паскале»: как вычислить. Примеры программ
Обучение программированию идёт по пути от простого к сложному. Освоив типы данных и операторы языка, переходят к циклическим конструкциям. Задач на циклы существует бесчисленное количество: начиная от вывода цифр в столбик до подсчёта сумм по сложным формулам. Тем не менее у начинающих программистов остаётся вопрос: «Как вычислить факториал в «Паскале»?»
Реализовать задачу можно как минимум тремя способами. Отличаются они используемыми операторами.
Математические сведения
Перед тем как перейти к построению алгоритмов и написанию программ, следует изучить теорию. В математике факториалом называют произведение целого числа, для которого вычисляется выражение, на целые положительные числа меньше его.
Понять определение поможет пример. Пусть требуется выполнить нахождение факториала для числа 3. Решение: 3! = 3 * 2 * 1 = 6.
Обозначается действие восклицательным знаком, который ставится после числа. Важное замечание: факториал определён только для целых положительных чисел. Вместе с тем, введено понятия для нуля: 0! = 1.
Считать выражение для больших значений вручную – занятие долгое. Чтобы убыстрить процесс вычислений, используют компьютерные программы. Далее рассмотрены способы, как найти факториал в «Паскале».
Первый способ
Код ниже показывает вариант программы.
В примере используют составную конструкцию с условием, которое записывается перед телом цикла. Синтаксис записи:
Выполняется код следующим образом: программа проверяет истинность выражения , в случае положительной проверки переходит на .
Возвращаясь к программе, нужно обратить внимание на следующие строки:
- 2 – задаётся число n, для которого будет выполнен расчёт;
- 6 – заголовок цикла;
- 7 – начало цикла;
- 8 – вычисление переменной fact, которая хранит значение факториала числа n;
- 9 – увеличение переменной-счётчика на единицу;
- 10 – конец цикла.
Второй способ
Следующий предлагает вычислить факториал в «Паскале» с помощью оператора repeat.
Конструкция цикла: repeat until <условие>;
Чтобы понять, как работает программа, рассмотрим её построчно:
- 2 – константе n назначается число, для которого выполняется вычисление;
- 7 – начало цикла;
- 8, 9 – расчёт факториала и увеличения счётчика i;
- 10 – конец тела цикла;
- 11 – проверка условия, поскольку условие располагается после последовательности операторов, повтор действий будет выполнен как минимум один раз.
Третий способ
Последняя программа также дает возможность вычислить факториал в «Паскале» и является самой компактной по размеру. Причина – используемый оператор for, для которого увеличение счётчика i задаётся в параметрах цикла.
Работает код следующим образом (цифрами указаны строки листинга):
- 2 – константе n присваивают значение числа, для которого вычисляется факториал;
- 6 – задаются параметры цикла – начальное и конечное значения;
- 7 – начало цикла;
- 8 – вычисление переменной fact;
- 9 – конец цикла.
Замечание
Даже для чисел из первой десятки факториал имеет значение больше, чем допускает тип данных integer. Поэтому программа в «Паскале» покажет сообщение об ошибке. Исправить её просто – нужно заменить тип данных для переменной-результата на longint или использовать типы для хранения вещественных значений.
Источник статьи: http://fb.ru/article/304034/faktorial-v-paskale-kak-vyichislit-primeryi-programm
Написать функцию вычисления факториала
Написать рекурсивную функцию вычисления факториала
Нужно написать рекурсивную функцию вычисления n!. Обычную функции могу написать, а куда рекурсию.
Написать программу, которая вычисляет значение p = (для вычисления факториала использовать функцию)
Написать программу, которая вычисляет значение p =m!*(m-n)!/n! (для вычисления факториала.
Вычисление суммы, используя функцию вычисления факториала
Составить программу вычисления суммы (рис), используя функцию вычисления факториала натурального.
Вычислить величины. Использовать функцию вычисления факториала
Составить программу. В задаче предполагается, используя шестизначный учебный шифр (его.
простите меня на недогадливость, а в чём состоит существенная экономия?
Решение
очень хитро!
я бы лично вряд ли использовал подобный код в реале (не люблю в продакшн такие хитрозакрученные и слегка неочевидные вещи), но код вызывает восхищение! Просто супер!
Спасибо!
bormant, а эта строчка всё таки НЕ НУЖНА! 
Закомментируйте и убедитесь в этом сами!
цикл for изменяет переменную m
Решение
Тут понимаете какая штука.
Для языка Паскаль недвусмысленно заявлено, что значение счетчика цикла for по окончании цикла не определено, если только цикл не завершился по Break. Это означает, что значение счетчика цикла может быть разным в зависимости как от реализации языка, так и от варианта оптимизации внутри конкретной реализации (например, равным последнему значению, следующему за последним значением, или вовсе начальному значению). Если какая-то реализация будет брать начальное значение счетчика из памяти в регистр, все обращения к счетчику транслировать в обращения к этому регистру, а возвращать значение из регистра в память только по Break, то, строго говоря, это не будет нарушением с точки зрения языка.
Поэтому закладываться на особенности той или иной реализации — самое последнее дело.
Это сродни самой дорогой ошибке программирования — ARIANE 5, с той лишь разницей, что там заложились не на языковые особенности, а на то, что начальные условия старта ARIANE 4, для которой изначально писался код, останутся неизменны.
Наоборот, код не использует ни одной нестандартной или недокументированной возможности. Он просто помнит одно последнее значение и использует его, если возможно. В конкретно этом примере экономия невелика, но представьте вместо Longint длинную арифметику, и оценки времени сразу заиграют новыми красками 🙂
Пример по сути является наводящим для организации «ленивых вычислений». Если последнее значение заменить таблицей, вычисляемой по мере необходимости, то достигается экономия на повторных вычислениях одних и тех же значений (без проверок допустимых диапазонов, только идея):
Или варианты с промежуточными значениями и довычисление от них необходимых.
Другое дело, что если бы в продакшн подобный участок был бы действительно критичным по времени, то вместо функции была бы таблица.
Источник статьи: http://www.cyberforum.ru/turbo-pascal/thread1795221.html
Алгоритмы быстрого вычисления факториала
Понятие факториала известно всем. Это функция, вычисляющая произведение последовательных натуральных чисел от 1 до N включительно: N! = 1 * 2 * 3 *… * N. Факториал — быстрорастущая функция, уже для небольших значений N значение N! имеет много значащих цифр.
Попробуем реализовать эту функцию на языке программирования. Очевидно, нам понадобиться язык, поддерживающий длинную арифметику. Я воспользуюсь C#, но с таким же успехом можно взять Java или Python.
Итак, простейшая реализация (назовем ее наивной) получается прямо из определения факториала:
На моей машине эта реализация работает примерно 1,6 секунд для N=50 000.
Далее рассмотрим алгоритмы, которые работают намного быстрее наивной реализации.
Алгоритм вычисления деревом
Первый алгоритм основан на том соображении, что длинные числа примерно одинаковой длины умножать эффективнее, чем длинное число умножать на короткое (как в наивной реализации). То есть нам нужно добиться, чтобы при вычислении факториала множители постоянно были примерно одинаковой длины.
Пусть нам нужно найти произведение последовательных чисел от L до R, обозначим его как P(L, R). Разделим интервал от L до R пополам и посчитаем P(L, R) как P(L, M) * P(M + 1, R), где M находится посередине между L и R, M = (L + R) / 2. Заметим, что множители будут примерно одинаковой длины. Аналогично разобьем P(L, M) и P(M + 1, R). Будем производить эту операцию, пока в каждом интервале останется не более двух множителей. Очевидно, что P(L, R) = L, если L и R равны, и P(L, R) = L * R, если L и R отличаются на единицу. Чтобы найти N! нужно посчитать P(2, N).
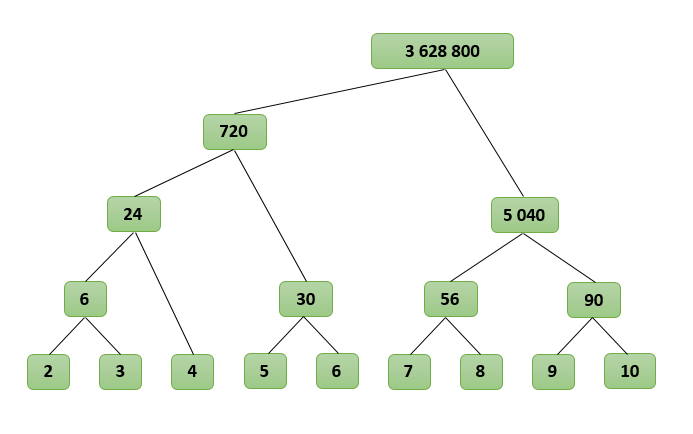
Посмотрим, как будет работать наш алгоритм для N=10, найдем P(2, 10):
P(2, 10)
P(2, 6) * P(7, 10)
( P(2, 4) * P(5, 6) ) * ( P(7, 8) * P(9, 10) )
( (P(2, 3) * P(4) ) * P(5, 6) ) * ( P(7, 8) * P(9, 10) )
( ( (2 * 3) * (4) ) * (5 * 6) ) * ( (7 * 8) * (9 * 10) )
( ( 6 * 4 ) * 30 ) * ( 56 * 90 )
( 24 * 30 ) * ( 5 040 )
720 * 5 040
3 628 800
Получается своеобразное дерево, где множители находятся в узлах, а результат получается в корне 
Реализуем описанный алгоритм:
Для N=50 000 факториал вычисляется за 0,9 секунд, что почти вдвое быстрее, чем в наивной реализации.
Алгоритм вычисления факторизацией
Второй алгоритм быстрого вычисления использует разложение факториала на простые множители (факторизацию). Очевидно, что в разложении N! участвуют только простые множители от 2 до N. Попробуем посчитать, сколько раз простой множитель K содержится в N!, то есть узнаем степень множителя K в разложении. Каждый K-ый член произведения 1 * 2 * 3 *… * N увеличивает показатель на единицу, то есть показатель степени будет равен N / K. Но каждый K 2 -ый член увеличивает степень еще на единицу, то есть показатель становится N / K + N / K 2 . Аналогично для K 3 , K 4 и так далее. В итоге получим, что показатель степени при простом множителе K будет равен N / K + N / K 2 + N / K 3 + N / K 4 +…
Для наглядности посчитаем, сколько раз двойка содержится в 10! Двойку дает каждый второй множитель (2, 4, 6, 8 и 10), всего таких множителей 10 / 2 = 5. Каждый четвертый дает четверку (2 2 ), всего таких множителей 10 / 4 = 2 (4 и 8). Каждый восьмой дает восьмерку (2 3 ), такой множитель всего один 10 / 8 = 1 (8). Шестнадцать (2 4 ) и более уже не дает ни один множитель, значит, подсчет можно завершать. Суммируя, получим, что показатель степени при двойке в разложении 10! на простые множители будет равен 10 / 2 + 10 / 4 + 10 / 8 = 5 + 2 + 1 = 8.
Если действовать таким же образом, можно найти показатели при 3, 5 и 7 в разложении 10!, после чего остается только вычислить значение произведения:
10! = 2 8 * 3 4 * 5 2 * 7 1 = 3 628 800
Осталось найти простые числа от 2 до N, для этого можно использовать решето Эратосфена:
Эта реализация также тратит примерно 0,9 секунд на вычисление 50 000!
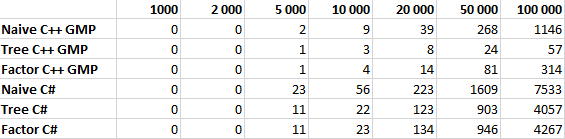
Как справедливо отметил pomme скорость вычисления факториала на 98% зависит от скорости умножения. Попробуем протестировать наши алгоритмы, реализовав их на C++ с использованием библиотеки GMP. Результаты тестирования приведены ниже, по ним получается что алгоритм умножения в C# имеет довольно странную асимптотику, поэтому оптимизация дает относительно небольшой выигрыш в C# и огромный в C++ с GMP. Однако этому вопросу вероятно стоит посвятить отдельную статью.
Все алгоритмы тестировались для N равном 1 000, 2 000, 5 000, 10 000, 20 000, 50 000 и 100 000 десятью итерациями. В таблице указано среднее значение времени работы в миллисекундах. 
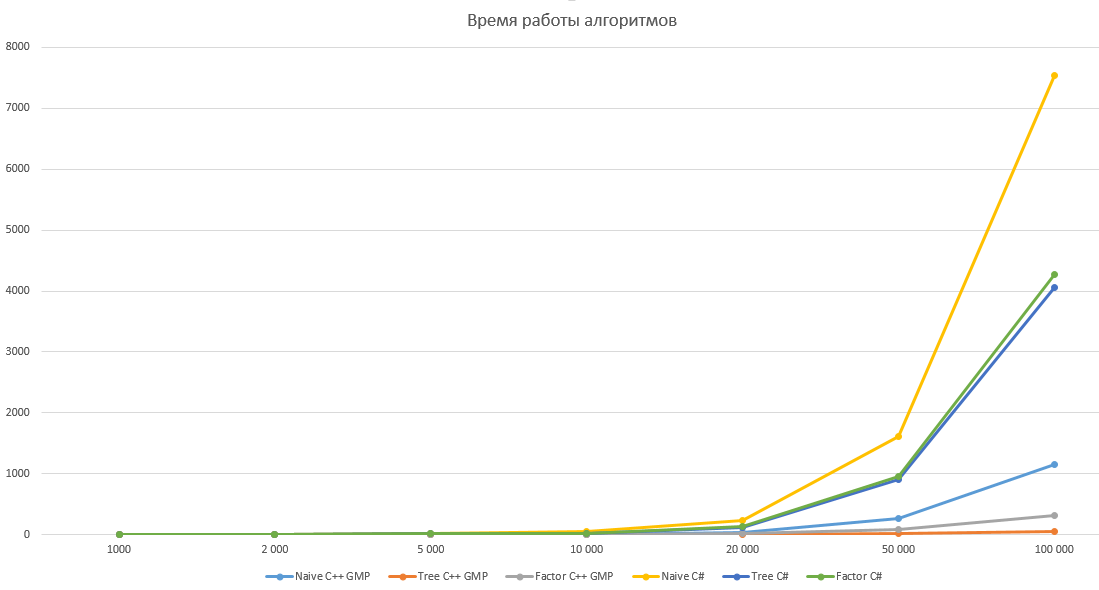
График с линейной шкалой 
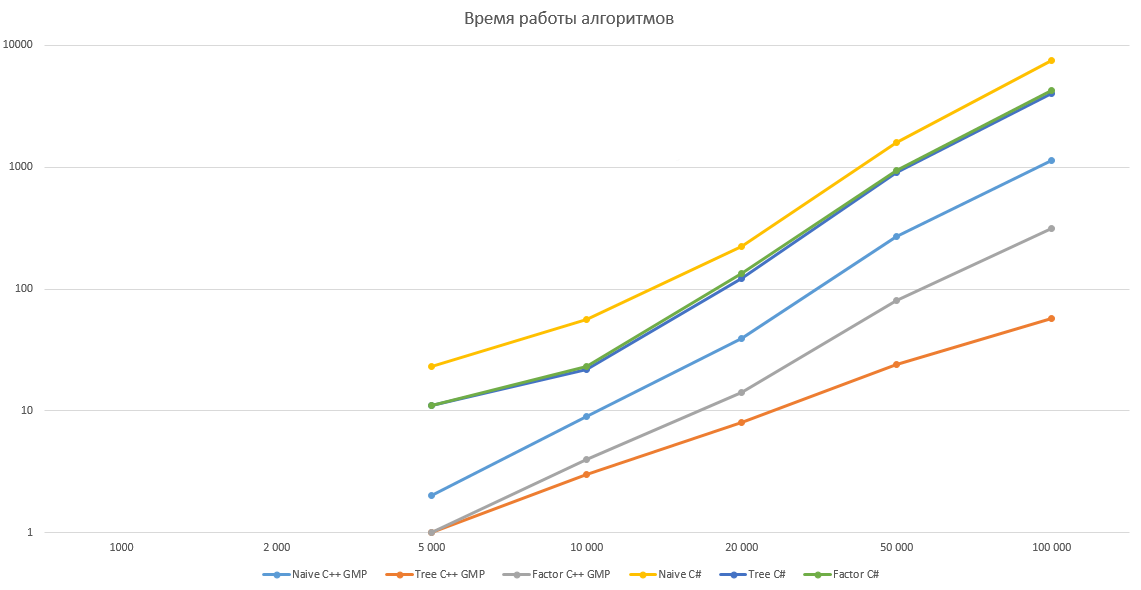
График с логарифмической шкалой 
Идеи и алгоритмы из комментариев
Хабражители предложили немало интересных идей и алгоритмов в ответ на мою статью, здесь я оставлю ссылки на лучшие из них
Исходные коды реализованных алгоритмов приведены под спойлерами
Источник статьи: http://habr.com/ru/post/255761/
Вычисление факториала
Здравствуйте Недавно начал изучать С++
Ну и столкнулся с проблемным заданием
Составить программу вычисления факториала введенного с клавиатуры числа. // результат вывести в таком виде: fact=1*2*3=6 ( при n =3)
Вроде ничего сложного но все равно не пойму
Вычисление факториала
ребята помогите решить. составьте пожалуйста код!) а) (m+1)!
Вычисление факториала
Написать программу, чтобы она циклически запрашивала ввод пользователем числа и считала его.
Вычисление факториала
В одном задании я столкнулся с факториал b(итое)=i/(i!) восклицательный знак это факториал я.
Вычисление факториала
Нужно заставить программу выводить результат, но почему то не получается #include .
А это зачем? Факториал нуля определен.
0! = 1
Это и по определению, и по здравому смыслу.
Добавлено через 1 минуту
Kuzia domovenok, Там еще требуется
Заказываю контрольные, курсовые, дипломные и любые другие студенческие работы здесь.
Вычисление факториала.
Помогите пожалуйста решить задачу!! Язык С++ Дано натуральное число n. Написать программу, которая.
Вычисление факториала
Написать функцию, которая возвращает факториал числа. Значение 0! принять равным 1 (0!=1!=1). Не.
Вычисление факториала
как реализовать вычисление факториала натурального числа с помощью рекурсивной функции?
Вычисление факториала
Помогите пожалуйста вычислить факториал:
Источник статьи: http://www.cyberforum.ru/cpp-beginners/thread2443282.html