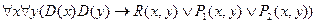ЗАНЯТИЕ 5. ПЕРЕВОД ВЫСКАЗЫВАНИЙ ЕСТЕСТВЕННОГО ЯЗЫКА НА ЯЗЫК ЛОГИКИ ПРЕДИКАТОВ
Из формализованных языков математики – язык логики предикатов – самый близкий к естественному. Работы по искусственному интеллекту используют именно этот язык, хотя у этого языка есть ограничения. При переводе высказываний естественного языка на язык исчисления предикатов необходимо понимать, что на языке логики предикатов можно описать многое, но далеко не все. Поэтому при символизации языка требуется аккуратность и глубокое понимание текста.
В естественном языке слово “все” обычно опускается.
Так, например, “Рыбы дышат жабрами” означает, что все рыбы дышат жабрами или, что каждая рыба дышит жабрами. Если обозначить 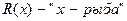
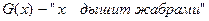
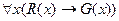
Однако не в каждом случае слова “все” понимаются как “каждый”. Например, предложение “Все песчинки образуют кучу песка” вовсе не означает, что каждая песчинка образует кучу песка. В этом случае употреблять квантор всеобщности 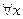
Рассмотрим особенности перевода на язык исчисления предикатов следующих выражений: “Все студенты отличники” и “Некоторые студенты отличники”.
Первое выражение может быть перефразировано так: “Для всех 



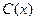

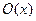

Второе выражение может быть перефразировано так: “Для некоторых 


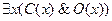




Вот еще один пример: “Собакам и кошкам вход запрещен”. Формально перевод будет таким: “Если 



кошкой, не существует. Правильным будет такой перевод:
“Если 


Для перевода высказываний естественного языка на язык логики предикатов можно использовать следующую таблицу
| Выражение естественного языка | Формула |
Для любого  (имеет место) (имеет место)   при произвольном при произвольном  Для всех Для всех  верно верно   , каково бы ни было , каково бы ни было  Для каждого Для каждого  (верно) (верно)  Всегда имеет место Всегда имеет место  Каждый обладает свойством Каждый обладает свойством  Свойство Свойство  присуще вcем Все удовлетворяет присуще вcем Все удовлетворяет  Любой объект является Любой объект является  Всякая вещь обладает свойством Всякая вещь обладает свойством  |  |
Для некоторых  (имеет место) (имеет место)  Для подходящего Для подходящего  (верно) (верно)  Существует Существует  , для которого (такой, что) , для которого (такой, что)  Имеется Имеется  , для которого (такой, что) , для которого (такой, что)  Найдется Найдется  , для которого (такой, что) , для которого (такой, что)  | 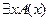 |
У некоторых вещей есть признак  Хотя бы для одного Хотя бы для одного  (верно) (верно)  Кто-нибудь относится к (есть) Кто-нибудь относится к (есть)  По крайней мере, один объект есть По крайней мере, один объект есть  | |
Не для каждого  (верно) (верно)  Не при всяком Не при всяком  (верно) (верно)   оказывается истинным не для всех оказывается истинным не для всех  Не все обладает свойством Не все обладает свойством  Не все суть Не все суть   не всегда верно не всегда верно | 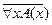 |
Для всякого  неверно неверно   всегда ложно Ничто не обладает свойством всегда ложно Ничто не обладает свойством  Все суть не Все суть не  | 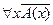 |
Не существует  , такого, что , такого, что  Нет никакого Нет никакого  , такого, что , такого, что  Нет Нет  , такого, что , такого, что   не выполняется ни для какого не выполняется ни для какого  Ничто не обладает свойством Ничто не обладает свойством  Никто не есть Никто не есть  Ни для какого Ни для какого  не верно не верно  Неверно, что для некоторых Неверно, что для некоторых   |  |
Для некоторого  не (верно) не (верно)  Что-то не обладает свойством Что-то не обладает свойством  Кто-то есть не Кто-то есть не  |  |
Если  для какого-нибудь для какого-нибудь  , то , то 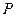 Если имеется Если имеется  , для которого , для которого  , то , то 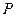 Если хоть что-нибудь есть Если хоть что-нибудь есть  , то , то 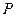 |  |
Если  , то для некоторого , то для некоторого  (верно) (верно)  | 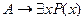 |
Что-то удовлетворяет  , а что-то – , а что-то – 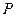 Нечто есть и Нечто есть и  и и 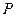 | 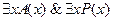  |
Все суть  или или 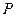 Все, кроме Все, кроме  , суть , суть 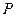 | 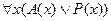 |
Все суть  или все суть или все суть 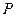 | 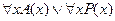 |
Как следует из таблицы, знак общности 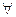
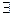
Для иллюстрации особенностей перевода рассмотрим еще несколько примеров.
Пусть 


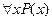

а) Не каждое простое число нечетное.
б) Найдется (существует) простое число, которое четно.
Для высказывания 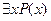

а) Не существует простого нечетного числа.
б) Все простые числа являются четными.
Способ а) построения отрицания в обоих случаях отличается от способа б) тем, что использует отрицательную частицу не, — это негативный способ построения отрицания.
В способе б) частица не использовалась – это позитивный способ построения отрицания. Негативный способ построения отрицания для высказывания 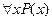
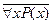
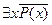
Для высказывания 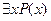
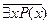
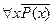
Равносильность двух способов построения отрицания следует из формул
Первая формула утверждает: 



Вторая формула утверждает: не существует 



Если высказывание содержит слова: все, каждый, любой, то при построении отрицания позитивным способом необходимо заменить их словами: найдется, существует, хотя бы один.
Если же в высказывании употребляются слова: найдется, существует, хотя бы один, то при построении отрицания они заменяются словами: все, каждый, любой.
Недопонимание этого правила приводит к типичной ошибке при построении отрицания.
Пример 1. Пусть 
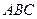
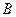
Отрицание для высказывания 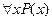
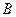
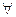
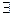
Правильная формулировка отрицания для высказывания 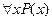
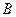
Пример 2. Пусть предикат 

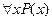
Рассмотрим несколько примеров по переводу высказываний естественного языка на язык исчисления предикатов.
Пример 1. Любые два действительных числа либо равны, либо одно из них меньше другого.
Введем в рассмотрение следующие предикаты:
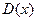

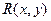
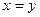
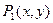
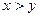
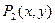
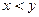
Тогда высказывание запишется в виде:
Пример 2. Ни один пациент не любит знахарей.
Введем в рассмотрение следующие предикаты:


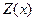

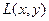


Тогда высказывание запишется в виде:
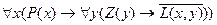
Пример 3. Представить на языке исчисления предикатов основные аксиомы натуральных чисел:
а) для каждого числа существует одно и только одно число, непосредственно следующее за ним;
б) нет числа, за которым непосредственно следует 0;
в) для каждого числа, отличного от нуля, существует одно и только одно непосредственно предшествующее ему число.
Введем в рассмотрение следующие предикаты:
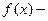

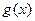

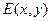
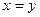
Тогда аксиомы будут представлены так:
а) 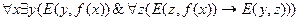
б) 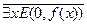
в) 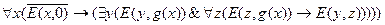
Контрольные вопросы и упражнения
Перевести выражения естественного языка на язык исчисления предикатов
1. Если произведение конечного числа сомножителей равно нулю, то, по меньшей мере, один из сомножителей равен нулю. ( 

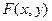


2. Наибольший общий делитель чисел 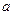
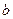
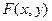


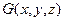
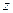


3. Для всякого действительного числа 

4. Существуют такие действительные числа 

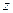



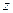
5. Для каждого действительного числа 

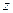
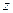


6. Существует x, меньшее, чем 5 и, большее, чем 3.
7. Для любого числа 


8. Для любых чисел 

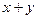
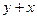
9. Для любого числа 

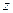
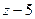

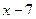
10. Между любыми двумя различными точками на прямой лежит, по крайней мере, одна точка, с ними не совпадающая.
11.Каждый студент выполнил, по крайней мере, одну лабораторную работу.
12.Если произведение натуральных чисел делится на простое число, то на него делится, по крайней мере, один из сомножителей.
13. Через три точки, не лежащие на одной прямой, проходит единственная плоскость.
14. Всякое животное, встречающееся с вежливыми людьми, счастливо.
15. Все люди, посещающие зоопарк, вежливы.
16. Животные, живущие в зоопарке, встречаются с людьми, посещающими зоопарк.
17. Никакой продавец игрушками сам себе их не покупает.
18. Те римляне, которые ненавидели диктатора, пытались убить его.
19. Римляне либо были преданы диктатору, либо ненавидели его.
20. Некоторые судьи — старики, но бодрые.
21. Судья Иванов не стар и не бодр.
23. Некоторые юристы, являющиеся политиками, – члены конгресса.
24. Ни один член конгресса не бодр.
25. Все старые члены конгресса — юристы.
26. Некоторые женщины одновременно являются юристами и членами конгресса.
27. Некоторые пациенты любят докторов.
29. Ни один доктор не является знахарем.
30. Выгул кошек или собак запрещен.
31. Ни одна женщина не является одновременно политиком и домашней хозяйкой.
32. Ни один судья не является преподавателем.
33. Некоторые женщины-юристы являются домашними хозяйками.
34.Все женщины-юристы восхищаются каким-нибудь судьей.
35. Некоторые юристы восхищаются только судьями.
36. Некоторые юристы восхищаются женщинами.
37. Некоторые преподаватели не восхищаются ни одним юристом.
38. Судья Иванов не восхищается ни одним преподавателем.
39. Существуют как юристы, так и преподаватели, которые восхищаются судьей Ивановым.
40. Только судьи восхищаются судьями.
41. Все судьи восхищаются только судьями.
42.Все студенты группы свободно владеют всеми тремя языками: английским, немецким, французским.
43. Каждый студент группы владеет каждым иностранным языком (английским, немецким, французским).
44. Есть студенты, которые свободно владеют и английским и немецким и французским языками.
45. В группе есть студенты, которые свободно владеют английским языком, есть те, которые свободно владеют французским, а также те, которые знают немецкий язык.
46. Нет столь великой вещи, которую не превзошла бы величиной еще большая.
47. Каждое рациональное число есть действительное число. Некоторое действительное числоесть рациональное
число. Не каждое действительное число есть рациональное число.
48. Пусть 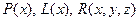
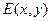
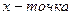
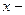
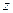


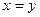
49. На всех кошек и собак следует получить разрешение.
50. Любые два действительных числа либо равны, либо одно из них меньше другого.
51. Каждый ребенок человека 

52. У человека 

53. Существуют два человека такие, что каждый ребенок одного из них состоит в браке с ребенком другого.
54. Существуют два человека такие, что ни один ребенок одного из них не состоит в браке с ребенком другого.
55. Если 



56. Введем следующие обозначения:
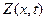

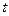
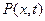

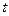
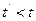

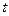
Перевести следующие выражения на язык исчисления предикатов
56.2. Иногда я ничего не вижу.
56.3. Существуют предметы, которые я никогда не вижу.
56.4. Я вижу каждую вещь в некоторый момент времени.
56.5. Если я вижу предмет, то я его тут же беру.
56.6. Если я вижу предмет, то я его беру спустя некоторое время.
56.7. Перед тем, как я беру предмет, я вижу его.
56.8. Если я беру предмет, не видя его до этого, то через некоторое время я вижу его, но не беру.
56.9. Не существует предметов, которые я никогда не беру.
56.10. Я никогда не беру того, что я всегда вижу.
56.11. Всегда существуют вещи, которые я не вижу и не беру.
56.12. Я беру всякую вещь, которую я никогда не вижу.
56.13. Я беру всякий предмет, который я еще не взял до этого.
56.14. Я всегда вижу либо все, либо ничего.
56.15. Если я беру некоторый предмет, который до этого уже видел, то я ранее видел предмет, который взял позднее.
56.16. Некоторые вещи, которые я видел ранее, я всегда вижу вновь спустя определенное время.
56.17. Если я когда-либо видел две вещи одновременно, то в будущем я также увижу их только одновременно.
56.18. Если я когда-либо видел и взял предмет одновременно, то впоследствии я либо делаю то и другое, либо не делаю ни того, ни другого.
Дата добавления: 2015-06-27 ; Просмотров: 12181 ; Нарушение авторских прав?
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник статьи: http://studopedia.su/19_48695_zanyatie—perevod-viskazivaniy-estestvennogo-yazika-na-yazik-logiki-predikatov.html