Как написать площадь квадрата

Как определить площадь квадрата

Формула нахождения площади квадрата

Квадрат это фигура, которая является частным случаем прямоугольника, из-за чего можно заметить схожесть некоторых алгоритмов. Способ вычисления всегда зависит от исходных данных. Чтобы узнать площадь квадрата, третьекласснику необходимо знать специальные формулы, рассмотрим пять из них.

Если известна длина стороны

Умножаем ее на то же число или возводим в квадрат.

S = a * a = a 2 , где где S — площадь, a — сторона.

Если нам дана диагональ

Возводим ее в квадрат и делим на два.

S = d 2 : 2, где где d — диагональ.

Если известен радиус вписанной окружности

Умножаем его квадрат на четыре.

S = 4 * r 2 , где r — это радиус вписанной окружности.

Если у нас есть радиус описанной окружности

Возведем его в квадрат и умножим на два.

S = 2 * R 2 , где R — это радиус описанной окружности.

Если есть периметр

Мы должны возвести его в квадрат и разделить на 16.

S = Р 2 :16, где Р — это периметр.

Периметр любого четырехугольника равен сумме длин всех его сторон.

Популярные единицы измерения:

квадратный миллиметр (мм 2 );
квадратный сантиметр (см 2 );
квадратный дециметр (дм 2 );
квадратный метр (м 2 );
квадратный километр (км 2 );
гектар (га).

S квадрата. Решение задач

Мы разобрали пять формул для вычисления площади квадрата. А теперь давайте потренируемся!

Задание 1. Как найти площадь квадрата, диагональ которого равна 90 мм.

Задание 2. Окружность вписана в квадрат. Как вычислить площадь квадрата, если радиус окружности равен 24 см.

Если окружность вписана в квадрат, то сторона квадрата равна диаметру.
Диаметр окружности равен двум радиусам.
Получается: сторона = 2 * радиус.
Используем формулу: S = сторона 2 .
Подставим значение стороны через радиус вписанной окружности:

Теперь подставим значение радиуса в формулу: S = 4 * 24 2 .

Ответ: S = 2304 см 2 .

Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики в детскую школу Skysmart. Наши преподаватели понятно объяснят что угодно — от дробей до синусов — и ответят на вопросы, которые бывает неловко задать перед всем классом. А еще помогут догнать сверстников и справиться со сложной контрольной.

Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем.

Источник статьи: http://skysmart.ru/articles/mathematic/ploshad-kvadrata

По какой формуле рассчитывается площадь квадрата?

Существует 5 формул для нахождения площади квадрата:

S=a⋅a=a2 — формула площади квадрата через сторону,
S = ½ d² — формула площади квадрата через диагональ,
S=4⋅r² — формула площади квадрата через радиус вписанной окружности,
S=2⋅R² — формула площади квадрата через радиус описанной окружности,
S= Р²/ 16 — формула площади квадрата через периметр квадрата.

Самый простой и быстрый способ — нужно возвести значение его стороны в квадрат. То есть умножить само на себя. Например, длина стороны равна 5 см. Умножаем 5*5, получаем 25 квадратных сантиметров 😃

Посчитать площадь квадрата можно через его диагональ по формуле: S = ½ d²,

где d — диагональ, т.е. отрезок, который соединяет два противоположных не смежных угла квадрата. Диагональ разделяет квадрат на два равных прямоугольных треугольника.

По какой формуле высчитывают периметр прямоугольника?

Периметр фигуры — это сумма длин ее сторон. Для простотого прямоугольника подойдет формула:

P=2*(a+b), a и b -длины прилегающих сторон прямоугольника.

Для правильного прямоугольника (квадрат), у которого все стороны равны, формулу можно упростить до:

P=4*a, где a — длина стороны квадрата.

Как уравнение может быть квадратным?

В алгебре квадратом числа называется результат умножения этого числа на само себя: так, например, квадратом числа 3 будет число 9 (3*3). Это же самое действие называют возведением в степень — в случае с вычислением квадрата числа это число возводят во вторую степень.

А уравнение называют квадратным потому, что в нем свободная переменная (например, x) стоит во второй степени — то бишь, в квадрате.

Как рассчитать количество обоев?

Для примера возьмем следующие исходные данные:

Длинна комнаты — 4 м.
Ширина комнаты — 3,2 м.
Высота потолка — 2,65 м.
Одна дверь — 85 см × 205 см.
Одно окно — 135 см × 135 см.
Обои — 10,05 м (длина) и 53 см (ширина).
Раппорт — 64 см.
Рисунок прямой, горизонтальная стыковка.

Начинаем клеить обои от окна на стене (4 м) без двери. Далее переходим на стену без окна (3,2). На эти две стены уйдет 13,58 полосы (остаток 0,42 полосы по ширине) (4+3,2) ⁄ 0,53.

Далее клеим стену с окном. Окно находится по центру, и от угла до окна 0,925 м — или почти 2 полосы обоев (106 см). По верху и низу окна на протяжении 106 см идут куски — их пока во внимание не берем. До следующего угла остается 108 см, или 2,02 полосы.

Считаем стену с дверью. Так как ширина двери не значительна, то ее даже в учет можно не брать. Получаем 7,54 полосы (остаток 0,46 полосы) (4 ⁄ 0,53).

Подводим итог:

13,58 округляем до 14 полос.
2 полосы.
7,54 округляем до 8 полос.
Итого 24 полосы или 8 трубок (с одной трубки выходит 3 полосы).
Остаются участки над и под окном — 2 полосы длинной 80 см и две полосы длиной 45 см. С учетом раппорта 64 см и запаса на выравнивание остатки из 8 трубок могут не покрыть требуемые участки. Поэтому, требуется дополнительная трубка.
Конечный итог — 9 трубок.
Результат, просчитанныйкалькулятором, также выдает 9 трубок.

Источник статьи: http://yandex.ru/q/question/hw.math/po_kakoi_formule_rasschityvaetsia_08ca155d/

Как найти площадь квадрата

Формула

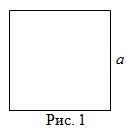
Чтобы найти площадь квадрата (рис. 1), надо длину его стороны возвести в квадрат, то есть

Напомним, что квадратом называется правильный четырехугольник, у которого все стороны и все углы равны.

Примеры вычисления площади квадрата

Задание. Найти площадь квадрата со стороной 3 см.

Решение. Площадь квадрата равна квадрату его стороны, то есть

Ответ. $S=3^2=9$ (см 2 )

Задание. Найти площадь квадрата, диагональ которого равна 2 м.

Решение. Известно, что сторона $a$ квадрата связана с его диагональю $d$ соотношением:

Ответ. $S=2$ (м 2 )

Разделы

Краткая теория

Онлайн калькуляторы

Другая информация

Рассчитайте цену решения ваших задач

Калькулятор
стоимости

Решение контрольной
300-600 рублей —> от 300 рублей *

* Точная стоимость будет определена после загрузки задания для исполнителя

Копирование материалов с сайта возможно только с разрешения администрации портала и при наличие активной ссылки на источник.

«Сегодня от своего лица хочу поблагодарить этот сайт за помощь мне с учебой. Здесь я пользовалась не только материалами, но и нашла преподавателей которые решали мне задачи.

Если тебе нужно что-то сделать в универе, я сама рекомендую. А также пользуйся моей ссылкой и получай 300 руб. на счёт при регистрации.»

Источник статьи: http://www.webmath.ru/poleznoe/formules_14_6.php

Площадь фигур

Две фигуры называют равными, если одну их них можно так наложить на другую, что эти фигуры совпадут.

Площади равных фигур равны. Их периметры тоже равны.

Площадь квадрата

Для вычисления площади квадрата нужно умножить его длину на саму себя.

S_EKFM = EK · EK

Формулу площади квадрата, зная определение степени, можно записать следующим образом:

Площадь прямоугольника

Для вычисления площади прямоугольника нужно умножить его длину на ширину.

S_ABCD = AB · BC

Нельзя вычислять периметр или площадь, если длина и ширина выражены в разных единицах длины.

Обязательно проверяйте, чтобы и длина, и ширина были выражены в одинаковых единицах, то есть обе в см, м и т.д.

Площадь сложных фигур

Площадь всей фигуры равна сумме площадей её частей.

Задача: найти площадь огородного участка.

Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя правило выше.

Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.

S_ABCE = AB · BC
S_EFKL = 10 · 3 = 30 м 2
S_CDEF = FC · CD
S_CDEF = 7 · 5 = 35 м 2

Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников.
S = S_ABCE + S_EFKL
S = 30 + 35 = 65 м 2

Ответ: S = 65 м 2 — площадь огородного участка.

Свойство ниже может вам пригодиться при решении задач на площадь.

Диагональ прямоугольника делит прямоугольник на два равных треугольника.

Площадь любого из этих треугольников равна половине площади прямоугольника.

АС — диагональ прямоугольника ABCD . Найдём площадь треугольников ABC и ACD

Вначале найдём площадь прямоугольника по формуле.

S_ABCD = AB · BC
S_ABCD = 5 · 4 = 20 см 2

S_ABC = S_ABCD : 2

S_ABC = 20 : 2 = 10 см 2

S_ABC = S_ACD = 10 см 2

Источник статьи: http://math-prosto.ru/?page=pages/area/area_figures.php

Площадь

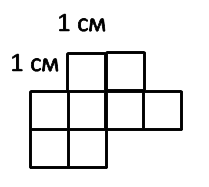
Вся фигура состоит из 8 квадратов со стороной 1 см каждый.

Площадь одного такого квадрата называют квадратным сантиметром и записывают: 1 см 2 .

Площадь всей фигуры 8 см 2 .

Площадь измеряется только в квадратных единицах длины. Всегда проверяйте свои ответы.

В математике для нахождения площади геометрических фигур используют специальные формулы, в которых площадь обозначается заглавной латинской буквой « S ».

Напоминаем, что площадь квадрата можно найти, умножив длину его стороны на саму себя.

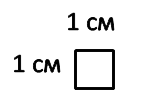
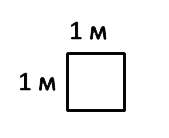
Единицей площади служит площадь единичного квадрата. Например, если длина стороны квадрата, равна 1 м, то его площадь равна 1 квадратному метру ( 1 м 2 ); если длина его стороны равна 1 см, то его площадь равна 1 квадратному сантиметру ( 1 см 2 ).

Для нахождения площади какой-либо фигуры её сравнивают с единичным квадратом.

Как перевести квадратные единицы

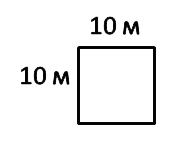
Рассмотрим квадрат со стороной 1 см.

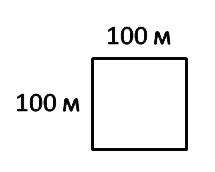
Рассмотрим квадрат со стороной 1 м.

1 м 2 = 1 м · 1 м = 100 см · 100 см = 10 000 см 2

Увеличим сторону квадрата равную 1 м в 10 раз. Получим квадрат со
стороной 10 м.

Площадь такого квадрата называют ар или сотка.

В одном аре — сто квадратных метров.

Слово «сотка» часто используют в дачном хозяйстве, хотя это тоже самое, что и «ар».

Чтобы выразить ар в cм 2 , вспомним, что 1 м 2 = 10 000 см 2 .

Значит: 1 ар (сотка) = 100 м 2 = 100 · 10 000 см 2 = 1 000 000 см 2

Увеличим сторону квадрата равную 10 м в 10 раз. Получим квадрат со
стороной 100 м.

Площадь такого квадрата называют гектар. Сокращенно «га». Но при произношении вслух наименование проговаривается полностью.

Выразим гектар в квадратных метрах.

1 га = 100 м · 100 м = 10 000 м 2

Теперь определим, сколько в одном гектаре аров.

Значит: 10 000 м 2 : 100 м 2 = 100 (ар)

Для измерения больших площадей, например, территорий государств, материков используют квадратный километр. То есть квадрат со стороной 1 км и
площадью 1 км 2 .

1 км 2 = 1 км · 1 км = 1 000 м · 1 000 м = 1 000 000 м 2

Для простоты расчётов предлагаем вам в помощь таблицу переводов квадратных единиц.

Таблица переводов квадратных единиц

Данная таблица поможет перевести гектары в кв. метры, гектары в ары и наоборот.

Источник статьи: http://math-prosto.ru/?page=pages/area/area.php