Параметрическое уравнение прямой на плоскости
В данной статье мы рассмотрим параметрическое уравнение прямой на плоскости. Приведем примеры построения параметрического уравнения прямой, если известны две точки этой прямой или если известна одна точка и направляющий вектор этой прямой. Представим методы преобразования уравнения в параметрическом виде в канонический и общий виды.
Параметрическое уравнение прямой L на плоскости представляется следующей формулой:
Отметим что при записи уравнения прямой в параметрическом виде, направляющий вектор прямой не должен быть нулевым вектором, т.е хотя бы один координат направляющего вектора q должен быть отличным от нуля.
Для построения прямой на плоскости в декартовой прямоугольной системе координат, заданной параметрическим уравнением (1), достаточно задать параметру t две разные значения, вычислить x и y и провести через эти точки прямую линию. При t=0 имеем точку M1(x1, y1) при t=1, получим точку M2(x1+m, y1+p).
Для составления параметрического уравнения прямой на плоскости L достаточно иметь точку на прямой L и направляющий вектор прямой или две точки, принадлежащие прямой L. В первом случае, для построения параметрического уравнения прямой нужно координаты точки и направляющего вектора вставить в уравнение (1). Во втором случае сначала нужно найти направляющий вектор прямой q=<m, p>, вычисляя разности соответствующих координатов точек M1 и M2: m=x2−x1, p=y2−y1(Рис.1). Далее, аналогично первому случаю, подставить координаты одной из точек (не имеет значение какой именно) и направляющего вектора q прямой в (1).
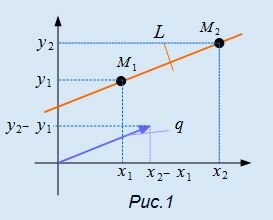 |
Можно также вывести формулу параметрического уравнения прямой, проходящей через две точки. Для этого подставим значения m=x2−x1, p=y2−y1 в (1), получим параметрическое уравнение прямой на плоскости, проходящей через точки M1(x1, y1) и M2(x2, y2):
Пример 1. Прямая проходит через точку M=(3,−1) и имеет направляющий вектор q=<−3, 5>. Построить параметрическое уравнение прямой.
Решение. Для построения параметрического уравнения прямой, подставим координаты точки и направляющего вектора в уравнение (1):
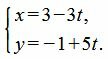 |
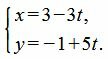 |
Пример 2. Прямая проходит через точки M1=(−5, 2) и M2=(−2, 3). Построить параметрическое уравнение прямой.
Решение. Воспользуемся формулой (2). Подставим координаты точек M1 и M2 в уравнение (2):
 |
Упростим полученное уравнение:
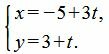 |
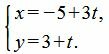 |
Приведение параметрического уравнения на плоскости к каноническому виду
Выразим параметр t в (1) через переменные x и y:
Из выражений (3), можем записать каноническое уравнение прямой на плоскости:
Обратное преобразование смотрите здесь.
Пример 3. Прямая на плоскости представлена следующим параметрческим уравнением:
 |
Привести данное уравнение прямой к каноническому виду.
Решение: Выразим параметр t через переменные x и y:
Из выражений (5), можем записать:
 |
 |
Приведение параметрического уравнения на плоскости к общему виду
Для приведения параметрического уравнения прямой на плоскости к общему виду, в формулах (1) выразим из второго уравнения параметр t через переменную y и подставим в первое уравнение:
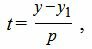 |
Умножим обе части уравнения (6) на p и группируем элементы уравнения:
Сделаем обозначения: A=p, B=−m, C=−px1+my1. Тогда получим общее уравнение прямой:
Обратное преобразование смотрите здесь.
Пример 4. Прямая на плоскости представлена следующим параметрческим уравнением:
Привести данное уравнение прямой к общему виду.
Решение: В уравнении (9) имеем: x1=−5, y1=0, m=4, p=−2. Подставим эти значения в формулу (7):
Упростив выражение (10) получим общее уравнение прямой (9):
Источник статьи: http://matworld.ru/analytic-geometry/parametricheskoe-uravnenie-prjamoj.php
Параметрические уравнения прямой на плоскости
Параметрические уравнения прямой элементарно получаются из канонического уравнения этой прямой, имеющей вид 

Так как один из знаменателей обязательно отличен от нуля, а соответствующий числитель может принимать какие угодно значения, то областью изменения параметра 

Мы получим 
Уравнения (1) и есть искомые параметрические уравнения прямой. Эти уравнения допускают механическую интерпретацию. Если считать, что параметр 

Пример 1. Составить на плоскости параметрические уравнения прямой, проходящей через точку 

Решение. Подставляем данные точки и направляющего вектора в (1) и получаем:
Часто в задачах требуется преобразовать параметрические уравнения прямой в другие виды уравнений, а из уравнений других видов получить параметрические уравнения прямой. Разберём несколько таких примеров. Для преобразования параметрических уравнений прямой в общее уравнение прямой сначала следует привести их к каноническому виду, а затем из канонического уравнения получить общее уравнение прямой
Пример 2. Записать уравнение прямой
Решение. Сначала приводим параметрические уравнения прямой к каноническому уравнению:
Дальнейшими преобразованиями приводим уравнение к общему виду:
Несколько более сложно преобразование общего уравнения в параметрические уравнения прямой, но и для этого действия можно составить чёткий алгоритм. Сначала можно преобразовать общее уравнение в уравнение с угловым коэффициентом и найти из него координаты какой-либо точки, принадлежащей прямой, придавая одной из координат произвольное значение. Когда известны координаты точки и направляющего вектора (из общего уравнения), можно записать параметрические уравнения прямой.
Пример 3. Записать уравнение прямой 
Решение. Приводим общее уравнение прямой в уравнение с угловым коэффициентом:
Находим координаты некоторой точки, принадлежащей прямой. Придадим одной из координат точки произвольное значение
Из уравнения прямой с угловым коэффициентом получаем другую координату точки:
Таким образом, нам известны точка 

Пример 4. Найти угловой коэффициент прямой, заданной параметрическими уравнениями
Решение. Параметрические уравнения прямой сначала следует преобразовать в каноническое, затем в общее и, наконец, в уравнение с угловым коэффициентом.
Таким образом, угловой коэффициент заданной прямой:
Пример 5. Составить параметрические уравнения прямой, проходящей через точку 
Решение. Cначала найдём из данных параметрических уравнений координаты вектора нормали искомой прямой. Если направляющий вектор 

Составим общее уравнение искомой прямой по формуле 
Преобразуем полученное уравнение в уравнение с угловым коэффициентом:
Находим какую-либо точку, принадлежащую этой прямой. Для этого одной из координат этой точки придадим произвольное значение 
Источник статьи: http://function-x.ru/line5.html
Уравнение прямой
Уравнение прямой на плоскости
Любую прямую на плоскости можно задать уравнением прямой первой степени вида
где A и B не могут быть одновременно равны нулю.
Уравнение прямой с угловым коэффициентом
Общее уравнение прямой при B≠0 можно привести к виду
где k — угловой коэффициент равный тангенсу угла, образованного данной прямой и положительным направлением оси ОХ.
Уравнение прямой в отрезках на осях
Если прямая пересекает оси OX и OY в точках с координатами ( a , 0) и (0, b ), то она может быть найдена используя формулу уравнения прямой в отрезках
Уравнение прямой, проходящей через две различные точки на плоскости
Если прямая проходит через две точки M( x 1, y 1) и N( x 2, y 2), такие что x 1 ≠ x 2 и y 1 ≠ y 2, то уравнение прямой можно найти, используя следующую формулу
| x — x 1 | = | y — y 1 |
| x 2 — x 1 | y 2 — y 1 |
Параметрическое уравнение прямой на плоскости
Параметрические уравнения прямой могут быть записаны следующим образом
где N( x 0, y 0) — координаты точки лежащей на прямой, a = < l , m >— координаты направляющего вектора прямой.
Каноническое уравнение прямой на плоскости
Если известны координаты точки N( x 0, y 0) лежащей на прямой и направляющего вектора a =
Решение. Воспользуемся формулой для уравнения прямой проходящей через две точки
Упростив это уравнение получим каноническое уравнение прямой
Выразим y через x и получим уравнение прямой с угловым коэффициентом
Найдем параметрическое уравнение прямой. В качестве направляющего вектора можно взять вектор MN .
Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем параметрическое уравнение прямой
Решение. Так как M y — N y = 0, то невозможно записать уравнение прямой проходящей через две точки.
Найдем параметрическое уравнение прямой. В качестве направляющего вектора можно взять вектор MN .
Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем параметрическое уравнение прямой
Уравнение прямой в пространстве
Уравнение прямой, проходящей через две различные точки в пространстве
Если прямая проходит через две точки M( x 1, y 1, z 1) и N( x 2, y 2, z 2), такие что x 1 ≠ x 2, y 1 ≠ y 2 и z 1 ≠ z 2, то уравнение прямой можно найти используя следующую формулу
| x — x 1 | = | y — y 1 | = | z — z 1 |
| x 2 — x 1 | y 2 — y 1 | z 2 — z 1 |
Параметрическое уравнение прямой в пространстве
Параметрические уравнения прямой могут быть записаны следующим образом
 | x = l t + x 0 |
| y = m t + y 0 | |
| z = n t + z 0 |
где ( x 0, y 0, z 0) — координаты точки лежащей на прямой,
Каноническое уравнение прямой в пространстве
Если известны координаты точки M( x 0, y 0, z 0) лежащей на прямой и направляющего вектора n =
| x — x 0 | = | y — y 0 | = | z — z 0 |
| l | m | n |
Прямая как линия пересечения двух плоскостей
Если прямая является пересечением двух плоскостей, то ее уравнение можно задать следующей системой уравнений
Источник статьи: http://ru.onlinemschool.com/math/library/analytic_geometry/line/














