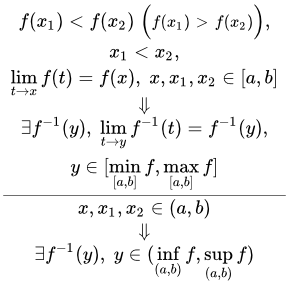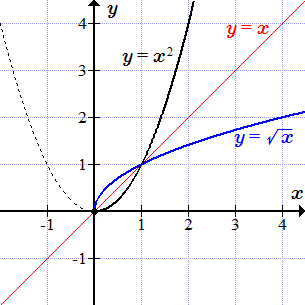Обратная функция
Что такое обратная функция? Как найти функцию, обратную данной?
Пусть функция y=f(x) определена на множестве D, а E — множество её значений. Обратная функция по отношению к функции y=f(x) — это функция x=g(y), которая определена на множестве E и каждому y∈E ставит в соответствие такое значение x∈D, что f(x)=y.
Таким образом, область определения функции y=f(x) является областью значений обратной к ней функции, а область значений y=f(x) — областью определения обратной функции.
Чтобы найти функцию, обратную данной функции y=f(x), надо :
1) В формулу функции вместо y подставить x, вместо x — y:
2) Из полученного равенства выразить y через x:
Найти функцию, обратную функции y=2x-6.
Функции y=2x-6 и y=0,5x+3 являются взаимно обратными.
Графики прямой и обратной функций симметричны относительно прямой y=x (биссектрисы I и III координатных четвертей).
y=2x-6 и y=0,5x+3 — линейные функции. Графиком линейной функции является прямая. Для построения прямой берём две точки.

Теорема (необходимое и достаточное условие обратимости функции)
Если функция y=f(x) определена и непрерывна на числовом промежутке, то для обратимости функции необходимо и достаточно, чтобы f(x) была строго монотонна.
Причем, если y=f(x) возрастает на промежутке, то и обратная к ней функция также возрастает на этом промежутке; если y=f(x) убывает, то и обратная функция убывает.
Если условие обратимости не выполнено на всей области определения, можно выделить промежуток, где функция только возрастает либо только убывает, и на этом промежутке найти функцию, обратную данной.
Классический пример — функция y=x². На промежутке [0;∞) функция возрастает. Условие обратимости выполнено, следовательно, можем искать обратную функцию.
Так как область определения функции y=x² — промежуток [0;∞), область значений на этом промежутке — также [0;∞), то область определения и область значений обратной функции — также [0;∞).
то есть на промежутке [0;∞) y=√x — функция, обратная к функции y=x². Их графики симметричны относительно биссектрисы I и III координатных четвертей:
В алгебре наиболее известными примерами взаимно обратных функций являются показательная и логарифмическая функция, а также тригонометрические и обратные тригонометрические функции.
1 комментарий
Для физических задач говорить об обратной функции, думаю, можно лишь для безразмерных у и х. При различии их размерностей, значит, и осей их графиков, надо для обратной функции поворачивать и оси.
Тогда лучше говорить о выражении аргумента х в явном виде, не упоминая об обратной функции. Значит, надо функцию у=ах/С+в, где х и С имеют, например, одинаковую размерность (например, кг), представить в виде уравнения ах/С+в-у=0. Из него можно выразить в явном виде у или х. Тогда либо у, либо х надо будет считать функцией с собственной координатной осью с собственной размерностью. При этом ось функции обычно является вертикальной.
Вопрос: можно ли считать выраженные в явном виде функции у и х обратными?
Источник статьи: http://www.algebraclass.ru/obratnaya-funkciya/
Обратная функция
Функция — это действие над переменной. Но что будет, если сделать действие — и обратное действие? Открыть дверь и закрыть дверь. Включить свет и выключить свет. Будет то же, что и было раньше, верно? Так и с функциями.
Функции f(x) и g(x) называются взаимно-обратными, если f(g(x)) = x.
Сделали действие (возвели в квадрат). Сделали обратное действие (извлекли квадратный корень). И получили то, что и было раньше, то есть переменную .
А вот . Подумайте, почему это так.
Другой пример взаимно-обратных функций: показательная и логарифмическая. Помните основное логарифмическое тождество: для . Для положительных х функции и являются взаимно-обратными.
Еще один пример взаимно-обратных функций:
Вспомним определение функции. Числовая функция y = f(x) — это такое соответствие между двумя числовыми множествами A и B, при котором каждому числу x ∈ A отвечает одно-единственное число y ∈ B. Множество A называется при этом областью определения функции, множество B — областью значений.
Пусть соответствие f является взаимно-однозначным:

Тогда существует функция g, которая действует в обратную сторону: каждому числу y ∈ B она ставит в соответствие одно-единственное число x ∈ A, такое, что f(x) = y:

Функция g называется обратной к функции f. Точно так же и функция f будет обратной к функции g.
Если мы возьмём какое-либо число x ∈ A и подействуем на него функцией f, то получим число y = f(x) ∈ B. Теперь на полученное число y подействуем функцией g. Куда попадём? Правильно, вернёмся к исходному числу x. Это можно записать так:
 | (1) |
Последовательное применение двух взаимно-обратных действий возвращает нас в исходную точку. Как и в жизни: сначала открыли дверь, а потом совершили обратное действие — закрыли дверь; в итоге вернулись к начальной ситуации.
Так, если возвести число 3 в степень x, а затем совершить обратное действие — взять от полученного числа 3 x логарифм по основанию 3 — мы вернёмся к исходному числу x:
Графики взаимно-обратных функций симметричны относительно прямой у = x.
То, что для функции является областью определения, для обратной функции будет областью значений.
Как вывести формулу обратной функции?
Если вы учитесь в математическом классе или на первом курсе вуза, вам может встретиться такое задание.
Например, у вас есть линейная функция Какая же функция будет к ней обратной?
Действуем следующим образом:
1) Выражаем из формулы функции x через у.
2) В формуле меняем x и у местами. Получаем формулу обратной функции:
Другой пример. Найдем обратную функцию для функции .
1) Выражаем из формулы функции x через у. Получаем:
2) В формуле меняем x и у местами. Получаем формулу обратной функции:
Источник статьи: http://ege-study.ru/obratnaya-funkciya/
Взаимно обратные функции
Функция, обратная данной
По определению (см. §34 справочника для 7 класса)
Функция – это соответствие, при котором каждому значению независимой переменной соответствует единственное значение зависимой переменной.
Пусть некоторое соответствие задано таблицей:
Множество значений X = <-4;-3;…;4>отображается в множество значений Y = <-2;-1,5;…;2>: $X \xrightarrow
С другой стороны, мы можем рассмотреть обратное отображение $Y \xrightarrow
Функцию $f: X \xrightarrow
Если функция f обратима, то обратное ей соответствие $g = f^<-1>$ называют обратной функцией к f.
Например: аналитическое выражение для функции $X \xrightarrow
Функция g — обратная функция к f.
В общем случае формулы функций записывают в виде y(x). При такой записи, функции $y = \frac
Алгоритм вывода формулы функции, обратной данной
На входе: множества X и Y, для которых оба соответствия $X \xrightarrow
Шаг 1. В формуле для исходной функции заменить обозначения аргумента и значения: $x \rightarrow y$, $y \rightarrow x$.
Шаг 2. Из полученной формулы выразить y(x). Искомое выражение для обратной функции найдено.
Шаг 3. Учесть ограничения для области определения и области значений исходной и/или обратной функций.
1) Пусть исходная функция $y = \frac
Шаг 1. Меняем аргумент и значение: $x = \frac
Шаг 2. Находим y из полученной формулы: y = 2x — искомая обратная функция
Шаг 3. Ограничений на x и y нет
2) Пусть исходная функция y = -2x+3
Шаг 1. Меняем аргумент и значение: x = -2y+3
Шаг 2. Находим y из полученной формулы: $y = \frac<-x+3><2>$ — искомая обратная функция
Шаг 3. Ограничений на x и y нет
3) Пусть исходная функция $y = \sqrt
Шаг 1. Меняем аргумент и значение: $x = \sqrt
Шаг 2. Находим y из полученной формулы: $y = x^2-1$ — искомая обратная функция
Шаг 3. На исходную функцию накладываются ограничения
на $x:x+1 \ge 0 \Rightarrow x \ge -1$, на $y:y \ge 0$
Тогда исходная функция определяется на множествах $y \ge -1$, $x \ge 0$
4) Пусть исходная функция $y = 2x^2+1$
Шаг 1. Меняем аргумент и значение: $x = 2y^2+1$
Шаг 2. Находим y из полученной формулы: $y = \sqrt<\frac
Шаг 3. На обратную функцию накладываются ограничения
на $x:x-1 \ge 0 \Rightarrow x \ge 1$, на $y:y \ge 0$
Тогда исходная функция определяется на множествах $y \ge 1$, $x \ge 0$
Исходная функция — парабола получает ограничения из-за обратной функции; только в этом случаи функции будут взаимно обратными.
Свойства взаимно обратных функций
Пусть f и g — взаимно обратные функции. Тогда:
1. Область определения функции f является областью значений функции g, а область значений функции f является областью определения функции g.
2. Функции f и g либо одновременно возрастающие, либо одновременно убывающие.
3. Если f — нечётная, то и g — нечётная.
4. Графики f и g симметричны относительно биссектрисы 1-й четверти y = x.
5. Справедливы тождества f(g(x) ) = x и g(f(x) ) = x.
Графики пар взаимно обратных функций, найденных выше:
 |  |
 |  |
Примеры
Пример 1. Задайте формулой функцию, обратную данной.
Меняем аргумент и значение: x = 5y-4
Получаем: $y = \frac
Меняем аргумент и значение: x = -3y+2
Получаем: $y = \frac<-x+2><3>$ — искомая обратная функция
Меняем аргумент и значение: x = 4y+1
Требуем, чтобы: $-1 \le y \le 5 \Rightarrow -1 \le \frac
Итак, искомая обратная функция: $y = \frac
г) $y=- \frac<1> <2>x+7$, где $2 \le x \le 9$
Меняем аргумент и значение: $x=-\frac<1> <2>y+7$
Требуем, чтобы: $2 \le y \le 9 \Rightarrow 2 \le -2x+14 \le 9 \Rightarrow -12 \le -2x \le -5 \Rightarrow$
$6 \ge x \ge 2,5 \Rightarrow 2,5 \le x \le 6$
$y = -2x+14,где 2,5 \le x \le 6$ — искомая обратная функция
Пример 2. Найдите функцию, обратную данной.
Постройте график исходной и обратной функции в одной системе координат.
$x = y^2 \Rightarrow y = \pm \sqrt
$y = — \sqrt
При этом $-1 \le y \le 4 \Rightarrow -1 \le x+3 \le 4$
y = x+3, $-4 \le x \le 1$ — искомая обратная
$x = \frac<1>
Область определения: $x \ge 3$
$x = 1+ \sqrt
Источник статьи: http://reshator.com/sprav/algebra/9-klass/vzaimno-obratnye-funkcii/
Обратные функции – определение и свойства
Определение и свойства
Определение обратной функции
Пусть функция имеет область определения X и множество значений Y . И пусть она обладает свойством:
для всех .
Тогда для любого элемента из множества Y можно поставить в соответствие только один элемент множества X , для которого . Такое соответствие определяет функцию, которая называется обратной функцией к . Обратная функция обозначается так:
.
Из определения следует, что
;
для всех ;
для всех .
Лемма о взаимной монотонности прямой и обратной функций
Если функция строго возрастает (убывает), то существует обратная функция , которая также строго возрастает (убывает).
Доказательство ⇓
Свойство о симметрии графиков прямой и обратной функций
Графики прямой и обратной функций симметричны относительно прямой .
Доказательство ⇓
Теорема о существовании и непрерывности обратной функции на отрезке
Пусть функция непрерывна и строго возрастает (убывает) на отрезке . Тогда на отрезке определена и непрерывна обратная функция , которая строго возрастает (убывает).
Доказательство ⇓
Для возрастающей функции . Для убывающей – .
Теорема о существовании и непрерывности обратной функции на интервале
Пусть функция непрерывна и строго возрастает (убывает) на открытом конечном или бесконечном интервале . Тогда на интервале определена и непрерывна обратная функция , которая строго возрастает (убывает).
Доказательство ⇓
Для возрастающей функции .
Для убывающей: .
Аналогичным образом можно сформулировать теорему о существовании и непрерывности обратной функции на полуинтервале.
Если функция непрерывна и строго возрастает (убывает) на полуинтервале или , то на полуинтервале или определена обратная функция , которая строго возрастает (убывает). Здесь .
Если строго возрастает, то интервалам и соответствуют интервалы и . Если строго убывает, то интервалам и соответствуют интервалы и .
Эта теорема доказывается тем же способом, что и теорема о существовании и непрерывности обратной функции на интервале.
Примеры обратных функций
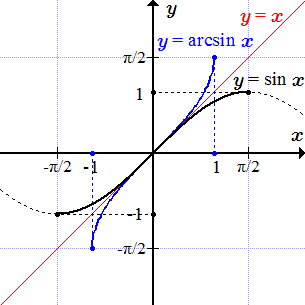
Арксинус
Рассмотрим тригонометрическую функцию синус: . Она определена и непрерывна для всех значений аргумента , но не является монотонной. Однако, если сузить область определения, то можно выделить монотонные участки. Так, на отрезке , функция определена, непрерывна, строго возрастает и принимает значения от –1 до +1 . Поэтому имеет на нем обратную функцию, которую называют арксинусом. Арксинус имеет область определения и множество значений .
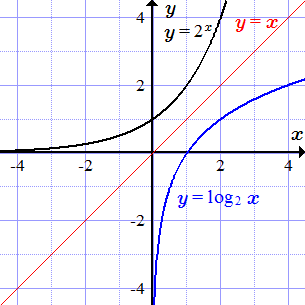
Логарифм
Показательная функция определена, непрерывна и строго возрастает при всех значений аргумента . Множеством ее значений является открытый интервал . Обратной функцией является логарифм по основанию два. Он имеет область определения и множество значений .
Квадратный корень
Степенная функция определена и непрерывна для всех . Множеством ее значений является полуинтервал . Но она не является монотонной при всех значений аргумента. Однако, на полуинтервале она непрерывна и строго монотонно возрастает. Поэтому если, в качестве области определения, взять множество , то существует обратная функция, которая называется квадратным корнем. Обратная функция имеет область определения и множество значений .
Пример. Доказательство существования и единственности корня степени n
Докажите, что уравнение , где n – натуральное, – действительное неотрицательное число, имеет единственное решение на множестве действительных чисел, . Это решение называется корнем степени n из числа a . То есть нужно показать, что любое неотрицательное число имеет единственный корень степени n .
Рассмотрим функцию от переменной x :
(П1) .
Докажем, что она непрерывна.
Используя определение непрерывности, покажем, что
.
Применяем формулу бинома Ньютона:
(П2)
.
Применим арифметические свойства пределов функции. Поскольку , то отлично от нуля только первое слагаемое:
.
Непрерывность доказана.
Докажем, что функция (П1) строго возрастает при .
Возьмем произвольные числа , связанные неравенствами:
, , .
Нам нужно показать, что . Введем переменные . Тогда . Поскольку , то из (П2) видно, что . Или
.
Строгое возрастание доказано.
Найдем множество значений функции при .
В точке , .
Найдем предел .
Для этого применим неравенство Бернулли. При имеем:
.
Поскольку , то и .
Применяя свойство неравенств бесконечно больших функций находим, что .
Таким образом, , .
Согласно теореме об обратной функции, на интервале определена и непрерывна обратная функция . То есть для любого существует единственное , удовлетворяющее уравнению . Поскольку у нас , то это означает, что для любого , уравнение имеет единственное решение, которое называют корнем степени n из числа x :
.
Доказательства свойств и теорем
Доказательство леммы о взаимной монотонности прямой и обратной функций
Пусть функция имеет область определения X и множество значений Y . Докажем, что она имеет обратную функцию. Исходя из определения ⇑, нам нужно доказать, что
для всех .
Допустим противное. Пусть существуют числа , так что . Пусть при этом . Иначе, поменяем обозначения, чтобы было . Тогда, в силу строгой монотонности f , должно выполняться одно из неравенств:
если f строго возрастает;
если f строго убывает.
То есть . Возникло противоречие. Следовательно, имеет обратную функцию .
Пусть функция строго возрастает. Докажем, что и обратная функция также строго возрастает. Введем обозначения:
. То есть нам нужно доказать, что если , то .
Допустим противное. Пусть , но .
Если , то . Этот случай отпадает.
Пусть . Тогда, в силу строгого возрастания функции , , или . Возникло противоречие. Поэтому возможен только случай .
Для строго возрастающей функции лемма доказана. Аналогичным образом можно доказать эту лемму и для строго убывающей функции.
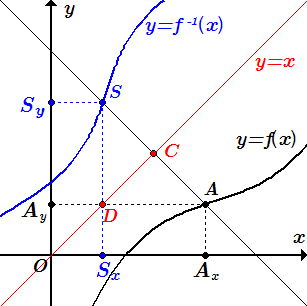
Доказательство свойства о симметрии графиков прямой и обратной функций
Пусть – произвольная точка графика прямой функции :
(2.1) .
Покажем, что точка , симметричная точке A относительно прямой , принадлежит графику обратной функции :
.
Из определения обратной функции следует, что
(2.2) .
Таким образом, нам нужно показать (2.2).
Из точек A и S опустим перпендикуляры на оси координат. Тогда
, .
Через точку A проводим прямую, перпендикулярную прямой . Пусть прямые пересекаются в точке C . На прямой строим точку S так, чтобы . Тогда точка S будет симметрична точке A относительно прямой .
Рассмотрим треугольники и . Они имеют две равные по длине стороны: и , и равные углы между ними: . Поэтому они конгруэнтны. Тогда
.
Рассмотрим треугольник . Поскольку , то
.
Тоже самое относится к треугольнику :
.
Тогда
.
Итак, уравнение (2.2):
(2.2)
выполняется, поскольку , и выполняется (2.1):
(2.1) .
Так как мы выбрали точку A произвольно, то это относится ко всем точкам графика :
все точки графика функции , симметрично отраженные относительно прямой , принадлежат графику обратной функции .
Далее мы можем поменять и местами. В результате получим, что
все точки графика функции , симметрично отраженные относительно прямой , принадлежат графику функции .
Отсюда следует, что графики функций и симметричны относительно прямой .
Доказательство теоремы о существовании и непрерывности обратной функции на отрезке
Пусть обозначает область определения функции – отрезок .
1. Покажем, что множеством значений функции является отрезок :
,
где .
Действительно, поскольку функция непрерывна на отрезке , то по теореме Вейерштрасса она достигает на нем минимума и максимума . Тогда по теореме Больцано – Коши функция принимает все значения из отрезка . То есть для любого существует , для которого . Поскольку и есть минимум и максимум, то функция принимает на отрезке только значения из множества .
2. Поскольку функция строго монотонна, то согласно вышеприведенной лемме ⇑, существует обратная функция , которая также строго монотонна (возрастает, если возрастает ; и убывает, если убывает ). Областью определения обратной функции является множество , а множеством значений – множество .
3. Теперь докажем, что обратная функция непрерывна.
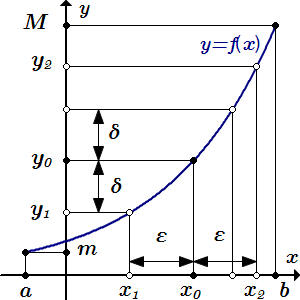
3.1. Пусть есть произвольная внутренняя точка отрезка : . Докажем, что обратная функция непрерывна в этой точке.
Пусть ей соответствует точка . Поскольку обратная функция строго монотонна, то есть внутренняя точка отрезка :
.
Согласно определению непрерывности нам нужно доказать, что для любого имеется такая функция , при которой
(3.1) для всех .
Заметим, что мы можем взять сколь угодно малым. Действительно, если мы нашли такую функцию , при которой неравенства (3.1) выполняются при достаточно малых значениях , то они будут автоматически выполняться и при любых больших значениях , если положить при .
Возьмем настолько малым, чтобы точки и принадлежали отрезку :
.
Введем и упорядочим обозначения:
.
Преобразуем первое неравенство (3.1):
(3.1) для всех .
;
;
;
(3.2) .
Поскольку строго монотонна, то отсюда следует, что
(3.3.1) , если возрастает;
(3.3.2) , если убывает.
Поскольку обратная функция также строго монотонна, то из неравенств (3.3) следуют неравенства (3.2).
Неравенства (3.3) определяют открытый интервал, концы которого удалены от точки на расстояния и . Пусть есть наименьшее из этих расстояний:
.
В силу строгой монотонности , , . Поэтому и . Тогда интервал будет лежать в интервале, определяемом неравенствами (3.3). И для всех значений , принадлежащих ему будут выполняться неравенства (3.2).
Итак, мы нашли, что для достаточно малого , существует , так что
при .
Теперь изменим обозначения.
Для достаточно малого , существует такое , так что
при .
Это означает, что обратная функция непрерывна во внутренних точках .
3.2. Теперь рассмотрим концы области определения. Здесь все рассуждения остаются теми же самыми. Только нужно рассматривать односторонние окрестности этих точек. Вместо точки будет или , а вместо точки – или .
Так, для возрастающей функции , . Обратная функция непрерывна в точке , поскольку для любого достаточно малого имеется , так что
при .
Обратная функция непрерывна в точке , поскольку для любого достаточно малого имеется , так что
при .
Для убывающей функции , .
Обратная функция непрерывна в точке , поскольку для любого достаточно малого имеется , так что
при .
Обратная функция непрерывна в точке , поскольку для любого достаточно малого имеется , так что
при .
Доказательство теоремы о существовании и непрерывности обратной функции на интервале
Пусть обозначает область определения функции – открытый интервал . Пусть – множество ее значений. Согласно приведенной выше лемме ⇑, существует обратная функция , которая имеет область определения , множество значений и является строго монотонной (возрастает если возрастает и убывает если убывает ). Нам осталось доказать, что
1) множеством является открытый интервал , и что
2) обратная функция непрерывна на нем.
Здесь .
1. Покажем, что множеством значений функции является открытый интервал :
.
Как и всякое непустое множество, элементы которого имеют операцию сравнения, множество значений функции имеет нижнюю и верхнюю грани:
.
Здесь и могут быть конечными числами или символами и .
1.1. Покажем, что точки и не принадлежат множеству значений функции. То есть множество значений не может быть отрезком .
Если или является бесконечно удаленной точкой: или , то такая точка не является элементом множества. Поэтому она не может принадлежать множеству значений.
Пусть (или ) является конечным числом. Допустим противное. Пусть точка (или ) принадлежит множеству значений функции . То есть существует такое , для которого (или ). Возьмем точки и , удовлетворяющие неравенствам:
.
Поскольку функция строго монотонна, то
, если f возрастает;
, если f убывает.
То есть мы нашли точку, значение функции в которой меньше (больше ). Но это противоречит определению нижней (верхней) грани, согласно которому
для всех .
Поэтому точки и не могут принадлежать множеству значений функции .
1.2. Теперь покажем, что множество значений является интервалом , а не объединением интервалов и точек. То есть для любой точки существует , для которого .
Согласно определениям нижней и верхней граней, в любой окрестности точек и содержится хотя бы один элемент множества . Пусть – произвольное число, принадлежащее интервалу : . Тогда для окрестности существует , для которого
.
Для окрестности существует , для которого
.
Поскольку и , то . Тогда
(4.1.1) если возрастает;
(4.1.2) если убывает.
Неравенства (4.1) легко доказать от противного. Но можно воспользоваться леммой ⇑, согласно которой на множестве существует обратная функция , которая строго возрастает, если возрастает и строго убывает, если убывает . Тогда сразу получаем неравенства (4.1).
Итак, мы имеем отрезок , где если возрастает;
если убывает.
На концах отрезка функция принимает значения и . Поскольку , то по теореме Больцано – Коши, существует точка , для которой .
Поскольку , то тем самым мы показали, что для любого существует , для которого . Это означает, что множеством значений функции является открытый интервал .
2. Теперь покажем, что обратная функция непрерывна в произвольной точке интервала : . Для этого применим предыдущую теорему ⇑ к отрезку . Поскольку , то обратная функция непрерывна на отрезке , в том числе и в точке .
Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Автор: Олег Одинцов . Опубликовано: 27-10-2018 Изменено: 23-11-2018
Источник статьи: http://1cov-edu.ru/mat-analiz/nepreryvnost-funktsii/obratnye-funktsii/