Разрабатываем алгоритмы действий и создаем блок-схемы
Разрабатываем алгоритмы действий и создаем блок-схемы
В жизни нам часто приходится встречаться с различными ситуациями, в которых мы совершаем одни и те же определенные действия. Для того, чтобы вовремя проснуться, нам нужно не забыть включить будильник. Для того, чтобы утолить свой голод, нам необходимо выполнить одни и те же действия по приготовлению вкусной пищи. Для того, чтобы выполнить знакомую нам работу, мы тоже часто делаем одно и то же.
Такое поведение можно называть по-разному, смотря в каком контексте оно рассматривается. Если рассмотреть с позиции эффективности деятельности, то эти действия можно назвать привычками или навыками. Если рассматривать с точки зрения отображения процесса, то описание последовательности действий, строгое исполнение которых приводит к решению поставленных задач за определенное количество шагов, называют алгоритмом действий.
Как создаются алгоритмы действий?
Мы постоянно сталкиваемся с этим в обычной жизни. Какие действия мы совершаем, чтобы пополнить счет своего мобильного телефона? Каждый из нас – разные. Так как способов пополнения счета несколько, следовательно мы все по-разному это делаем. Результат, правда всегда один получается – появление средств на телефоне.
Или еще пример: чтобы скопировать картинку или текст, нажимаем правой кнопкой мыши на картинку, затем выбираем “Копировать”, помещаем в нужное место, нажимаем правой кнопкой ” Вставить”, и результат достигнут.
Все это – определенная последовательность действий, в результате которых различными средствами решается поставленная задача. Но пока это только наши знания, которые перерастают в навыки и умения, а если этот процесс описать, то мы сможем наглядно увидеть алгоритм наших действий, и передать его другим людям. На словах не все и не всегда понятно бывает.
Опишите последовательность действий – это запоминается
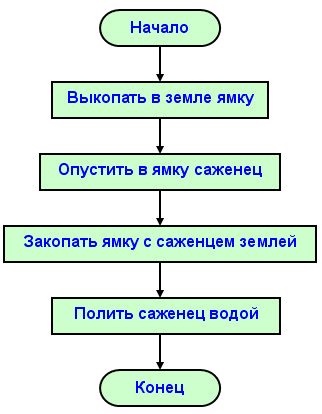
Создать алгоритм действий можно, описав или изобразив его последовательность. Знают ли все, что надо сделать, чтобы посадить дерево? Возможно, основные шаги понятны всем, но вот когда деревце поливать, перед посадкой или после, помнит не каждый. Созданный алгоритм позволит все действия выполнить в правильной последовательности.
Чтобы описать последовательность действий посложнее, придется постараться и подробно их все записать. Пример можно взять с всевозможных правил и инструкций – там очень четко прописываются по шагам действия, которые нам надо сделать. Но бывают ситуации, в которых за определенным действие следует не один шаг, а несколько, в зависимости от предыдущего результата. В таком случае, предположительные действия тоже записывают, чтобы человек мог легко сориентироваться в разных ситуациях, и знал, что нужно предпринять.
Алгоритм действий в графике – это блок-схема
Если изобразить алгоритмы действий в графическом варианте, с помощью геометрических фигур с линиями-связями, показывающими порядок выполнения действия, то мы получим блок-схему. Блок-схема намного превосходит правила, инструкции, и записанные по порядку алгоритмы действий, по своей наглядности и читаемости.
Представьте, что вам нужно чему-то научить другого человека. Вы отлично знаете все действия в определенной последовательности. Ваша задача – показать, как это нужно делать и передать свои знания так, чтобы другой человек их запомнил и знал так же, как и вы. Устная передача знаний допускает импровизации и некоторый произвол. Самым лучшим способом будет блок-схема, в которой объясняется последовательность и возможные варианты действий. В качестве примера – веселое руководство по изучению блог-схем:
Блок-схемы применяются в продажах
В продажах такое обучение с помощью разработки алгоритмов и изображения их в виде блок-схем имеет большое распространение. Чаще всего их используют в телефонных сценариях разговоров в call-центрах и для “холодных” звонков. Корпоративная культура набирает обороты, поэтому многие компании уже не позволяют сотрудникам нести “отсебятину”, даже талантливую, а предлагают действовать им по заранее разработанному сценарию, представляя “лицо фирмы” на различных этапах. Эффект появляется буквально после нескольких дней действий “по бумажке”. Со временем, многое из описанных алгоритмов запоминается сотрудником, и в дальнейшем он свободно может общаться, не опасаясь того, в какую сторону может уйти разговор.
Алгоритмы действий и блог-схемы разрабатываются не только в продажах. Большое распространение они имеют в обучении и практике врачей, программистов, “компьютерщиков”, у многих технических специальностей.
Стоит попробовать научиться действовать по подобным блок-схемам. Ведь впервые встречаясь с непонятным поначалу обилием действий и задач, думаешь о том, как тебе не хватает разработанной блок-схемы. После долгих мучений не выдерживаешь, и начинаешь разрабатывать и создавать самостоятельно. Эффективные люди не любят простоев в делах. А блок-схемы значительно упрощают жизнь и позволяют разобраться в решении сложных задач.
Сервисы для разработки блок-схем
В интернете есть сервисы, которые могут помочь вам создавать такие блок-схемы. Один из них – [urlspan]Сacoo[/urlspan]. С его помощью вам легко удастся превращать ваши алгоритмы в различные диаграммы, блок-схемы и графики. Вы увидите, что это очень приятное и радостное занятие – преобразовывать то, что вам известно, в науку для других людей.
На этом онлайн-сервисе – хорошее настроение вам обеспечено. На первоначальном этапе можно воспользоваться возможностями бесплатной учетной записи, а в будущем за доступ нужно будет платить. Естественно, что бесплатный доступ имеет ограничения по сравнению с платными. Но для изучения и первых шагов, функционала вполне достаточно.
Разработав алгоритмы действий и преобразовав их в блок-схемы с помощью Cacoo, вы сможете надолго создать хорошее настроение не только себе, но и другим людям, постигающим азы.
Создавайте игровые блок-схемы для своих детей
Подводя итог вышесказанному отмечу, что теперь вы сможете использовать алгоритмы действий и блок-схемы в различных жизненных ситуациях. Даже ваши дети с огромным удовольствием станут выполнять не самые интересные обязанности, следуя понятным подсказкам. Если будут идеи, где и как можно применять алгоритм действий, поделитесь в комментариях, уважаемые читатели. Очень хотелось бы узнать про ваши алгоритмы.
Моя блок-схема
Вот какая блок-схема у меня получилась в первый раз. Для того, чтобы увеличить изображение, нажмите на него. После перехода на Cacoo, под записью “просмотр фигуры”, нажимайте на картинку. Она откроется в большом окне. Удачи!
Успевайте больше за меньшее время вместе с “Копилкой эффективных советов”.
Источник статьи: http://kopilkasovetov.com/programmyi-servisi-prilogeniya/razrabatyivaem-algoritmyi-deystviy-i-sozdaem-blok-shemyi
Примеры составления алгоритмов
Определение 1.4. Под алгоритмизацией понимают процесс разработки алгоритма решения какой-либо задачи.
Для некоторых задач этот процесс достаточно прост, для других — требует определенных усилий, особенно в тех случаях, когда алгоритм должен удовлетворять наперед заданным условиям, например максимальному быстродействию решения задачи, минимальному требованию к объему памяти ЭВМ и др. В настоящем параграфе на примерах многих задач от простейших до относительно сложных изложены способы рационального составления алгоритмов. Задачи представлены в математической или почти в математической форме. При этом они подобраны так, что их решение не требует тех знаний, которые выходят за пределы курса математики общеобразовательных средних школ.
Опыт обучения программированию показывает, что студенты весьма часто пренебрегают составлением блок-схем алгоритмов. Желание быстрее написать программу порождает ощущение, что рисование блок-схемы как бы лишняя работа. Такой подход однако ошибочен и должен подавляться в самом начале обучения.
Составление блок-схемы до начала программирования очень часто позволяет обнаружить ошибки в решении задачи, тем самым уточнить алгоритм и в значительной степени избавиться от трудоемкого поиска ошибок при отладке программы. Практический опыт программирования свидетельствует о том, что большая доля времени, отведенного на составление программы, затрачивается программистами на обнаружение логических ошибок, а квалифицированными программистами считаются те из них, которые быстрее всего устраняют эти ошибки. В этой связи роль составления блок-схем алгоритмов чрезвычайно важна.
Кроме того, блок-схемы нужны для предоставления отчетности по разработкам, а также для ознакомления с ними заинтересованных лиц. Поэтому в дальнейшем для большинства рассматриваемых задач будут приведены либо блок-схемы алгоритмов, либо дана текстовая их форма, либо представлено и то и другое.
Теперь непосредственно перейдем к рассмотрению задач и конструированию алгоритмов их решения.
Задача 1.1. Даны два действительных числа а и Ь. Необходимо найти их сумму 5, разность Я, произведение Р и частное Н от деления а на Ь.
Алгоритм кажется очевидным: ввести в память ЭВМ числа а и Ь, выполнить вычисления 5 = а + Ь, Я = а — Ь, Р= а : Ь, Н = а/Ь и вывести на экран (принтер) полученные результаты. Однако такой алгоритм ошибочен для случая, когда Ь = 0. В этом случае чисто математически мы могли бы записать, что Н- а/Ь = со. Однако в компьютере операция деления на нуль не определена, вследствие чего на экране дисплея будет выведено сообщение «деление на нуль» и вычисление программы прервано. Поэтому проверка, равно ли Ь нулю, в алгоритме должна быть предусмотрена. Правильный алгоритм приведен на рис. 1.3. Ниже дана текстовая его форма.
Шаг 2. Вычислить Б = а + Ь, Я = а — Ь, Р= аЬ.
Шаг 4. Если Ь = 0, перейти к шагу 7.
Шаг 6. Вывести Н и перейти к шагу 8.
Задача 1.2. Даны два действительных положительных числа а и Ь. Найти среднее арифметическое и среднее геометрическое этих чисел.
Как известно, среднее арифметическое чисел а, Ь определяется как ?= <а+ Ь)/2, а среднее геометрическое как С =у[аЬ. Поэтому блок-схема алгоритма представлена на рис. 1.4. Текстовая его форма будет такой.
Шаг 2. Вычислить ?= (а + Ь)/2, С = 4аЬ.
Рис. 1.3. Алгоритм выполнения арифметических действий над действительными
Рис. 1.4. Алгоритм вычисления среднего арифметического и среднего геометрического двух чисел
Шаг 3. Вывести (7. Шаг 4. Остановиться.
В приведенном алгоритме записана операция среднего геометрического (7 = 4аЬ. Казалось бы, следовало вначале вычислить значение с=аЬ, а затем, используя, например, алгоритм Ньютона (см. рис. 1.1), вычислить (7. Однако в наборе стандартных программ компьютера имеется программа, вычисляющая квадратный корень из положительного числа. Поэтому при соответствующем обращении к этой программе она и вычислит (7.
Задача 1.3. Даны два действительных числа а и Ь. Определить, какое из чисел большее или они равны. Алгоритм решения задачи изображен на рис. 1.5.
Текстовая его форма такая.
Шаг 2. Если а = Ь, перейти к шагу 6.
Шаг 3. Если а > Ь, перейти к шагу 5.
Шаг 4. Вывести Ъ> а и перейти к шагу 7. Шаг 5. Вывести а> Ь и перейти к шагу 7. Шаг 6. Вывести а = Ь.
Вычислить значение функции 1 —х, если* 3 . если 2 2 , если 1 2 , еслих > 3.
Алгоритм вычисления ? представлен на рис. 1.6. Текстовая его форма следующая.
Шаг 2. Если х 2 и перейти к шагу 9.
Шаг 6. Вычислить ? = V1 + х 3 и перейти к шагу 9.
Шаг 7. Вычислить ?= 1/х 2 и перейти к шагу 9.
Задача 1.5. Составить алгоритм вычисления корней квадратного уравнения ах 2 + Ьх + с = Ос действительными коэффициентами а, Ь, с ф 0, когда а ф 0, Ь ф0, с ф0.
Как известно, в зависимости от знака дискриминанта с1 = Ь 2 — 4 ас квадратное уравнение ах 2 + Ьх + с = Ос действительными коэффициентами а, Ь, сф 0 может иметь три типа корней: разные действительные корни, если с1> 0, равные действительные корни, если с!= 0, и комплексные сопряженные корни, если с! 2 — 4ас, к = а + а, к = -Ь/к.
Шаг 3. Если 0, перейти к шагу 6.
Шаг 5. Положить х, = к и перейти к шагу 10.
Шаг 6. Вычислить g = 4(4, г = g/h, хх = к + г, х2 = к — г и перейти к шагу 9.
Шаг 8. Вывести: «Корни комплексные х, = /:+/>, х2 = /:-/>» и перейти к шагу 11.
Шаг 9. Вывести: «Корни действительные» х,, х2 и перейти к шагу 11.
Шаг 10. Вывести: «Корни, равные х, = х2» х,.
Большинство приведенных алгоритмов содержат так называемые разветвления, т. е. места в блок-схемах, где вычисления направляются по разным путям. Эти места определяются блоками сравнения величин. Из каждого блока имеется два выхода, один из которых соответствует тому случаю, когда условие сравнения выполняется («да»), другой — случаю, когда оно не выполняется («нет»). Такие алгоритмы называются алгоритмами с разветвляющейся структурой.
Теперь рассмотрим алгоритмы, которые содержат фрагменты повторения вычислений — циклы. В зависимости от того, известно ли наперед число повторений некоторого участка алгоритма или нет, различают циклы арифметические и итерационные.
В арифметических циклах число повторений вычислений контролируется с помощью управляющей переменной, играющей роль счетчика циклов. При каждом очередном вычислении значение счетчика изменяется на заданную величину и сравнивается с установленным количеством повторений. Если эти величины совпадают, повторения прекращаются, т. е. осуществляется выход из цикла по счетчику. В противном случае повторения вычислений продолжаются. Если перед началом цикла значение счетчика превышает заданное число повторений, он не выполняется вообще. Возможен также принудительный выход из цикла по некоторому наперед заданному условию.
В циклах итерационного типа, в которых число повторений наперед неизвестно, их прекращение (выход из цикла) осуществляется при выполнении некоторого условия. Обычно это условие формулируется, например, так: выполнять повторения до тех пор, пока х с, повторения вычислений не будет вообще, для второй всегда выполнится хотя бы один цикл. Все арифметические циклы — это циклы с предусловием.
Задача 1.6. Дан ряд чисел х15 х2. х,-, . хп. Найти их сумму 5.
Так как сумма 5 = х, + х2 + . + х,- + . + хп и суммирование чисел выполняется последовательно, т. е. к найденной сумме 5М добавляется х,- число, то вычисление 5, = 5М + х,- повторяется п — 1 раз, если положить 5М =хх. Поэтому алгоритм вычисления суммы будет таким, как изображен на рис. 1.8. Текстовая его форма включает следующие действия.
Шаг 4. Если/> п, перейти к шагу 7.
Шаг 6. Положить / = / + 1 и вернуться к шагу 4.
Рис. 1.8. Алгоритм вычисления суммы п чисел
В этом алгоритме роль счетчика циклов отводится переменной /, которая изменяется с шагом 1. Если бы требовалось вычисление суммы чисел х>, . хп через одно число, то очевидно, что шаг изменения переменной / должен быть взят равным 2, а начальное ее значение 3. Таким образом, в четвертом блоке схемы алгоритма следовало бы указать /= 3, а в седьмом / = /’ + 2.
Задача 1.7. Составить алгоритм вычисления функции п («л-факториал»). Как известно, п — это произведение п натуральных чисел 1 • 2 • 3 •. • п. При этом принимают, что 1! = 1. Поэтому вычисление значения п можно рассматривать как последовательное повторение операции умножения предшествующего значения факториала Т 7 на очередное натуральное число. Алгоритм вычисления п приведен на рис. 1.9.
Его текстовая форма такая.
Шаг 4. Если / > п, перейти к шагу 7.
Шаг 6. Положить /= /+ 1 и вернуться к шагу 4.
Аналогичным образом можно построить алгоритмы вычисления значений 2″, а п , где а — вещественное, а п — целые числа.
Задача 1.8. Составить алгоритм вычисления выражения к = = ^2 + ^2
+ ^2 + . + л/2 . Нетрудно видеть, что если в качестве
начального значения взять к = а/2 , то повторяющимся действием будет вычисление выражения V2 + к. Поэтому алгоритм решения этой задачи имеет вид, изображенный на рис. 1.10. Его текстовая форма такая.
Шаг 4. Если/> п, перейти к шагу 7.
Шаг 6. Положить /’=/’+ 1 и вернуться к шагу 4. Шаг 7. Вывести к.
Задача 1.9. Составить алгоритм вычисления выражения S = = sin л: + sin 2 * . + sin»*.
Если взять начальное значение суммы S = s’mx, то повторяющимся действием будет 5 + 5sin*. Алгоритм, вычисляющий указанную сумму, представен на рис. 1.11. Его текстовая форма такая.
Шаг 4. Если/> п, перейти к шагу 7.

Шаг 5. Вычислить S =S + ^sinx.
Шаг 6. Положить / = / + 1 и вернуться к шагу 4. Шаг 7. Вывести S.
Задача 1.10. Составить алгоритм вычисления среднего квадратического п действительных чисел ху, х2, . хп.
Известно, что средним к вадратическим п действительных
чисел является величина 5* = Л -(х? + х + . + х 2 п. Поэтому ал-
горитм будет таким (рис. 1.12). Его текстовая форма включает следующие действия.
Шаг 3. Если/> п, перейти к шагу 7.
Шаг 6. Положить /=/-+- 1 и вернуться к шагу 3.
Шаг 9. Вывести Шаг 10. Остановиться.
Задача 1.11. Составить алгоритм вычисления числа сочетаний п чисел по т для п > т > 0.
Число сочетаний из п по т, обозначаемое С» ! , вычисляется
алгоритма не вызывает проблем: вычислить значения п,
- (п — т), т, используя для этого алгоритм (см. рис. 1.9), а затем реализовать формулу для определения С”’. Такой подход в общем требует выполнения п — 1 + (п — т — 1) + т — 1 = 2/7-3 циклов. Имеется возможность сконструировать алгоритм вычисления значения С;, который будет выполнять всего т циклов. Тогда, в худшем случае, когда т всего лишь на единицу меньше п, число циклов будет примерно в 2 раза меньше 2/7. Этот алгоритм основан на использовании рекуррентного сотношения для вычисления С»‘.
- ?
Рис. 1.12. Алгоритм вычисления среднего квадратического
Для построения алгоритма запишем общее выражение для вычисления С» ! , которое будем вычислять в цикле. Согласно рекуррентному соотношению при т = 0 число сочетаний С^ 1 = С 1 =
С’”, Сп = п и позволяет вычислять сочетания последовательно С =п, С 2 = ——-С’п,
С’п. Так как в итоге необходимо получить зна
чение С»‘ т т — 1, перейти к шагу 11.
Шаг 8. Положить /= /+ 1 и вернуться к шагу 6.
Шаг 9. Положить С= 1 и перейти к шагу 11.
Заметим, что в приведенной блок-схеме предусмотрен контроль правильности ввода чисел т так, чтобы п> т.
Задача 1.12. Сконструировать алгоритм вычисления многочлена (полинома) Рп(х) степени п для некоторого действительного значения х
Используя традиционную форму представления многочлена рп(х) =апх п + ап_хх п
было бы изобразить, как на рис. 1.14.
Рис. 1.14. Алгоритм вычисления полинома, представленного
В этом алгоритме в цикле используются две операции умножения и одна операция сложения. Существует, однако, другой более быстрый способ вычисления значения многочлена. Он основан на использовании схемы Горнера, согласно которой полином представляется следующим образом:
Например, для п = 4 он имеет такой вид:
Алгоритм, вычисляющий полином по схеме Горнера, приведен на рис. 1.15. В цикле он выполняет всего одну операцию умножения.
Задача 1.13. Разработать алгоритм табулирования функции у = /(х) на интервале [а, Ь], а я, перейти к шагу 10.
Шаг 7. Положить х = х + Ах, вычислить у = Дх).
Шаг 9. Положить /= /’+ 1 и вернуться к шагу 6.
Алгоритм решения задачи с применением итерационного цикла приведен на рис. 1.17.
В этом алгоритме шаги 7, 8 проверяют, совпадает ли последняя точка табуляции функции со значением конца интервала Ь.
Задача 1.14. Составить алгоритм поиска наибольшего общего делителя (НОД) двух целых чисел a, b и наименьшего общего кратного (НОК) этих чисел.
Как известно, НОД чисел a, b — такое наибольшее целое число, которое делит эти числа без остатка. Наименьшим общим кратным целых чисел а, b является целое число, которое делится на а и Ь. Если известен НОД, то НОК вычисляется по следующей формуле: НОК (а, b) = ab/Oj(a, b). Поэтому прежде чем вычислять НОК, необходимо найти НОД.
Существует несколько алгоритмов вычисления НОД. Приведем простейший из них, который принадлежит древнегреческому математику Евклиду. Он заметил, что НОД (а, b) равен НОД ((а — b), Ь), где а > Ь. Поэтому суть его алгоритма сводится к последовательному вычитанию из большего числа меньшего до тех пор, пока эти числа станут равными между собой. Алгоритм приведен на рис. 1.18 и содержит цикл итерационного типа.
Текстовая форма алгоритма вычисления НОД, НОК следующая.
Шаг 3. Если а = Ь, перейти к шагу 7.
Шаг 4. Если а> Ь, перейти к шагу 6.

Рис. 1.17. Алгоритм табулирования функции /(х) с использованием
Рис. 1.18. Алгоритм вычисления наибольшего общего делителя чисел а, Ь и наименьшего их кратного
Шаг 5. Положить х = а, а = Ь, Ь = х.
Шаг 6. Положить х = а — Ь, а = х и вернуться к шагу 3.
Шаг 8. Вычислить НОК = и • г/НОД.
Шаг 9. Вывести а, Ь, НОД, НОК. Шаг 10. Остановиться.
Задача 1.15. Разработать алгоритм вычисления значения цеп-
Как следует из записи дроби, последним в ней делителем яв-
ляется выражение С=х + —, значение которого при задан- ном х легко может быть найдено. Предпоследним делителем яв-
х щим ему делителем является выражение С =х + — , где С —
найденное перед этим значение делителя. Таким путем может
быть найдено значение делителя С =х + — , а затем значение дроби У = —.
Очевидно, что повторяющимся действием в этой задаче является поиск очередного делителя. Учитывая, что 2 = 2 1 , а 256 = 2 8 , всего необходимо найти восемь делителей. Исключая последний делитель, всего получаем семь повторяющихся действий. На основании изложенных рассуждений конструируем алгоритм, вычисляющий заданное выражение (рис. 1.19). Его текстовая форма такая.
Шаг 2. Положить а = хх, Ь = 256.
Шаг 5. Если і min, перейти к шагу 8.
Шаг 7. Положить min = ак, j = к.
Этот алгоритм в худшем случае, т. е. когда число не обнаружено, выполняет 2п сравнений. Вместе с тем есть алгоритм, который при п > 8 заметно сокращает это число, а следовательно, и время поиска. Улучшенный алгоритм приведен на рис. 1.22. Уменьшение количества сравнений достигается за счет исключения постоянных сравнений / с п, характерных для первого алгоритма. Выход из цикла осуществляется либо когда а, = Ь, либо когда на (п+ 1)-м повторении обнаружится число Ь, записанное в (п + 1)-й ячейке массива.
Последние две задачи относят к задачам обработки массивов — наборов данных одного вида — чисел или символов. В программировании различают массивы одномерные и многомерные. Одномерный массив образуют последовательные его элементы. Место элемента в массиве определяется его номером — индексом, представляющим собой положительное число. Рассмотренные последовательности чисел а., аъ
Ь являются одномерными массивами.
Двумерные массивы — это прямоугольные таблицы данных, состоящие из заданного количества строк и колонок (столбцов). В математике такие таблицы называются матрицами и весьма широко используются как непосредственно при математических вычислениях, так и в программировании. Элемент матрицы размещается на пересечении строки и столбца и идентифицируется двумя индексами: номером строки, например /, и номером столбца, например у. Если матрица содержит т строк и п столбцов, всего элементов этой матрицы тп и а] — произвольный ее элемент. Матрица, содержащая т строк и т столбцов, называется прямоугольной.
В квадратной матрице выделяют главную и побочную диагонали. Матрица А = ац размером т х п, т. е. содержащая т строк
и п столбцов, т = п, имеет вид:
Главную диагональ матрицы образуют элементы аи, а22, . атп, т. е. элементы, лежащие на прямой, проведенной слева направо от элемента ап к элементу атп.
Побочную диагональ образуют элементы матрицы а1п, а2п_х, . ат1, лежащие на прямой, проведенной от элемента а1п к элементу ат<, т. е. справа налево.
Элементы матрицы А, лежащие справа и вверху от главной диагонали, образуют верхнюю треугольную матрицу. Элементы, лежащие слева внизу от главной диагонали, образуют нижнюю треугольную матрицу.
Матрица называется симметричной, если элементы, симметричные относительно главной диагонали, равны между собой, т. е. а и = й/ ( .
Одной из важнейших задач обработки одномерных массивов является их сортировка — расположение элементов массивов в определенном порядке. Чаще всего рассматривается упорядочение элементов числовых массивов по возрастанию или убыванию. По статистическим данным, примерно 25 % времени работы ЭВМ расходуется на сортировку данных, потому что отсортированные данные обрабатывать значительно проще. Когда элементы массива отсортированы, их быстрее найти, обновить, исключить из массива и т. п.
Существует целый ряд алгоритмов сортировки. Среднее время их работы или временная сложность лежит в пределах от 0(п 2 /4) до 0(ппп), где п — число элементов массива. К сожалению, нет алгоритма сортировки, который был бы наилучшим в любом случае.
Рассмотрим простейшую сортировку, называемую сортировкой вставками. Идея этой сортировки состоит в том, что очередной (сортируемый) элемент массива, упорядочиваемого, например, по возрастанию, сравнивается с предшествующими его элементами до тех пор, пока не встретится элемент, меньший или равный ему. Тогда все элементы, следующие за меньшим элементом, сдвигаются на одну позицию вправо, а очередной элемент ставится на освободившееся место за меньшим элементом. Если же в результате сравнения сортируемого элемента с предшествующими элементами массива меньший элемент не будет обнаружен, сортируемый элемент оставляют на старом месте и переходят к очередному элементу массива. Сравнения начинают со второго элемента массива и заканчивают последним его элементом.
Рассмотрим эту сортировку на массиве целых чисел
- 71 27 412 81 59 14 273 87, который требуется упорядочить по возрастанию. Первым сортируемым элементом массива является второй элемент — число 27. Образно говоря, «вынимаем» его из массива, т. е. освобождаем место для будущего сдвига чисел вправо, и сравниваем второй элемент (число 27) с первым элементом (число 71). Так как 27 71, а 71 > 21, оставляем число 412 на своем месте, т. е. получаем прежний массив
27 71 412 81 59 14 273 87.
Выбираем четвертый элемент массива — число 81. Запоминаем его и сравниваем с предшествующим элементом — числом 412. Так как 81 59, сдвигаем его на одну позицию вправо. Нетрудно видеть, что процесс сравнения и сдвига элементов закончится на числе 27. В результате получим
27 59 71 81 412 14 273 87.
Шестым элементом массива является число 14. Путем сравнения его с предшествующими элементами и сдвигов их вправо получим массив
14 27 59 71 81 412 273 87.
Выполнив описанные действия с седьмым и восьмым элементами массива, получим отсортированный список
14 27 59 71 81 87 273 412.
Задача 1.18. Разработать алгоритм сортировки вставками.
Согласно изложенному методу сортировки общим повторяющимся действием является выбор очередного сортируемого элемента и его запоминание. Элементы выбираются, начиная со второго и заканчивая последним п-м элементом массива. Эти действия составят внешний цикл алгоритма. Внутренний цикл алгоритма образуют действия сравнения и, если необходимо, сдвига элементов, а также его вставки в необходимую позицию массива. Поэтому алгоритм, реализуемый рассматриваемым методом, будет иметь такой вид (рис. 1.23). Его текстовая форма следующая.
Шаг 5. Если к > ар перейти к шагу 8.
Шаг 6. Если у 0 в приведенной блок-схеме необходима для того, чтобы при сравнении сортируемого элемента к с предшествующими ар я-_,, я, не выйти за пределы массива. Иначе алгоритм не будет определен. В заключение отметим, что сортировка вставками согласно [7] достаточно эффективна для массивов с максимальным количеством элементов п 3/2 ), и быстрой сортировке, средняя сложность которой 0(1п(я)). Как правило, такая сортировка применяется для массивов с числом элементов п > 1000.
В тех случаях, когда в некотором массиве постоянно осуществляется поиск элементов, этот массив предварительно сортируется и в дальнейшем поиск осуществляется в упорядоченном
Рис. 1.23. Алгоритм сортировки элементов массива вставкой
массиве. В качестве алгоритма поиска чаще всего используется так называемый бинарный поиск. Практика показывает, что такой подход существенно уменьшает средние временные затраты на поиск.
Суть бинарного поиска следующая. Пусть задан упорядоченный по возрастанию массив чисел ах, а2, ап ап и число Ь. Требуется найти элемент массива ак, равный Ь, или сообщить, что такого элемента в массиве нет. Обозначим первый индекс массива /, а последний и. Тогда индекс у числа ар стоящего примерно в середине массива, может быть найден по выражению у = |(/ + и)/2_|, где символы |_ ] определяют целую часть числа (/ + и)/2. Если
я- = Ь, процесс поиска завершен. Если же Ь ар то по той же причине число следует искать в подмассиве яу+1, . ап. Таким образом, в результате выбора числа а] и сравнения его с числом Ь можно перейти к поиску в массиве с числом элементов, меньших в 2 раза, чем п. Далее процесс выбора элемента я. осуществляется в одном из подмассивов, сокращая поиск в массиве с числом элементов, меньших в 2 раза, чем в подмассиве. Этот процесс выбора а] и деления очередного массива пополам продолжается до тех пор, пока не будет найдено заданное число либо установлено, что его в массиве нет. Описанный процесс продемонстрируем на поиске элемента Ь = 59 в следующем массиве
14 27 59 71 81 87 273 412 501.
Массив содержит девять элементов, поэтому у = |_(1 + 9)/2_| =
= 5. Элемент с индексом 5 — это а5 = 81. Сравниваем его с Ь = 59. В результате переходим к поиску в массиве 14 27 59 71 (/= 1, и =у — 1 = 5 — 1 = 4). Теперь вычисляем индекс у = |_(1 + 4)/2_| = 2.
Элемент с индексом 2 — это а2 = 27. Сравниваем его с Ь = 59. В результате переходим к поиску в массиве 59 71 (/=у+1 =
= 2+1 = 3, и = 4). Вычисляем индекс у = |_(3 + 4)/2_| = 3. Элемент
с индексом 3 — это я3 = 59. Сравниваем его с Ь = 59 и устанавливаем, что это искомый элемент массива.
Теперь рассмотрим случай, когда элемент Ь= 12, т. е. он не принадлежит массиву. Первый индекс у = 5 и мы переходим к поиску в массиве 14 27 59 71 (/ = 1, и = 4). Второй индекс у = 2, что дает очередной массив поиска 14 27 (/= 1, и = 2). Третий индекс поиска у = 1(1 + 2)/2 I = 1 и мы переходим к массиву поиска 14
(/ = 1, и = 0). Однако в массиве нет элемента с индексом и = 0. Это означает, что мы проверили весь массив и не нашли элемента я;= Ь. Таким образом, можно сделать вывод, что признаком отсутствия элемента в массиве служит неравенство и х — х — 2 = 0, и известно, что его корень принадлежит интервалу [а, Ь. Требуется найти значение этого корня.
В общем виде уравнение может быть записано как /(х) = 0, где Дх) — непрерывная функция, рассматриваемая на интервале [а, Ь]. Поскольку решение уравнения, т. е. его корень, х е [а, Ь] обращает уравнение в тождество, то левая часть равенства /(х) = 0 в точке х е а,Ь] должна быть равна нулю. С геометрической точки зрения это означает, что функция /(х) в точке х пересекает ось абсцисс. Эту точку пересечения и необходимо найти.
Для этого поступаем следующим образом. По выражению IV= (а + Ь)/2 находим координату IVсередины отрезка [а, Ь. Если Дх) = 0, то корень уравнения х= IV найден. Если /(а)/(ВО > 0, т. е. /(а) и /(ВО одного знака, корня на интервале нет (рис. 1.25), и мы переходим к его поиску на интервале [IV, Ь], который вполовину короче исходного интервала [а, Ь]. Если /(а)/(ВО 0, мы сокращаем интервал поиска ровно вдвое. В результате после п таких действий получим интервал [ап, Ьп], которому принадлежит корень уравнения, в 2″ раз меньший исходного интервала [а, Ь, т. е. ап — Ьп = а — ^/2″. Приняв в качестве точности вычисления корня а длину интервала |ап — Ьп, можно определить, что для получения этой точности необходимо сделать п = па — Ь|/е шагов. Описанный метод по-
Рис. 1.25. Иллюстрация к уточнению корня методом половинного деления
иска корня получил название метода половинного деления, или дихотомии.
Задача 1.20. Разработать алгоритм уточнения корня уравнения /(х) = 0 методом дихотомии.
Метод предполагает, что задан интервал а, Ь, которому принадлежит корень, функция /(х) = 0 непрерывна и ограничена на этом интервале и f(a) f(b) а + , w = f(x).
Шаг 4. Если w = 0, перейти к шагу 10.
Шаг 5. Если uw> 0, перейти к шагу 7.
Шаг 6. Положить b = x, v=w и перейти к шагу 8.
Шаг 8. Если а — Ь > с, вернуться к шагу 3.
При решении различных задач часто приходится использовать значения элементарных функций, таких как sin (х), cos (х), log (х), In (х), е х и др. Для того чтобы облегчить процесс вычис-
Рис. 1.26. Алгоритм вычисления корня уравнения /(х) = 0 методом дихотомии
ления этих функций, в системной библиотеке компьютера хранятся заранее составленные программы вычисления их значений. Для их использования достаточно лишь упомянуть имя функции и указать ее аргумент. В свою очередь указанные программы составлены на основании формул разложения той или иной функции в ряд. Например, функция е х представляется сле-
дующим бесконечным рядом е х = 1 + X +-+
Для функций sin (х), cos (х) соответственно имеем:
В каждом из указанных разложений точность представления той или иной функции определяется числом членов ряда. Чем больше это число, тем точнее вычисляется функция при одном и том же х. Поэтому для вычисления значения функции с заданной точностью с поступают следующим образом. Вычисляют и суммируют члены ряда до тех пор, пока очередное слагаемое не станет по модулю меньше 8.
Звдача 1.21. Составить алгоритм вычисления функции зт(х) с точностью 8 при помощи разложения ее в ряд.
Из формулы, которая приближенно представляет функцию бш(х) в виде бесконечного ряда, следует, что алгоритм вычисления значения 8ш(х) с заданной точностью е будет включать повторяющиеся действия вычисления очередного члена ряда, суммирования членов ряда и изменения знака перед соответствующим членом ряда. Нетрудно видеть, что каждый очередной член ряда Уп и может быть вычислен по рекуррентной формуле Уп =
Знаки членов ряда меняются поочередно, если начинать с Ух.
Поэтому начальными установками алгоритма будут такие ?=х, 6’ = х, Z= хх, а = —1. В цикле будем вычислять очередной
член ряда ? =— и прибавлять его к предшествующей
сумме с соответствующим знаком. Блок-схема алгоритма приведена на рис. 1.27. Его текстовая форма дана ниже.
Рис. 1.27. Блок-схема вычисления значения функции 8Іп(х)
Положить у = х, 5 = х, Z= хх, а = Положить п= 1.
Как было сказано раньше, след матрицы — это сумма эле-
ментов ее главной диагонали, т. е. Я, — ^аи. Поэтому алгоритм
определения следа сводится к вычислению суммы Блок-схема этого алгоритма приведена на рис. 1.28.
Вместе с тем есть способ построить более эффективный алгоритм решения этой задачи. Он основан на вычислении адреса очередного диагонального элемента матрицы А не в двумерном, а в одномерном массиве.
Известно, что элементы двумерных и больших измерений массивов в памяти компьютера записываются линейно. Ниже в качестве примера приведена линейная запись элементов матрицы А с тремя строками и столбцами.
Через индексы строк и столбцов /, у номер любого элемента в линейном массиве вычисляется по формуле х = (/ — 1)я+/ Например, номер элемента а22 определяется так (2 — 1)3 + 2 = 5. Таким образом, чтобы выбрать какой-либо элемент из линейного
Рис. 1.28. Алгоритм вычисления следа матрицы А
массива, необходимо вычислять его номер по выражению А / ‘= (/— 1 )п + у, т. е. выполнить три арифметические операции.
В то же время можно видеть, что номер очередного диагонального элемента в линейном массиве отличается от номера предшествующего диагонального элемента на постоянную величину к = п + 1. Например, номер а22 — 5 равен номеру ап — 1, т. е. 1 +4 = 5. Поэтому в линейном массиве очередной диагональный элемент определяется по номеру / = / + к. В результате его вычисление требует выполнить вместо трех всего одну арифметическую операцию, что в целом приводит к уменьшению объема вычислений и повышению быстродействия алгоритма. Блок-схема этого алгоритма приведена на рис. 1.29.
Задача 1.23. Разработать алгоритм вычисления суммы элементов побочной диагонали квадратной матрицы А.
В качестве примера рассмотрим матрицу с тремя строками и
Рис. 1.29. Эффективный алгоритм вычислени следа матрицы А
диагонали этой матрицы для их выделения проведена прямая линия. Первый индекс диагональных элементов — это номер строки /, второй, как нетрудно видеть, вычисляется по выражению у = п + 1 — /’, где к — п + 1. Поэтому блок-схема алгоритма, решающего эту задачу, будет иметь вид, представленный на рис. 1.30. Его текстовая форма приведена ниже.
Рис. 1.30. Блок-схема алгоритма вычисления суммы элементов побочной
диагонали квадратной матрицы А
Шаг 1. Ввести п, элементы матрицы А.
Шаг 2. Положить ? = 0, / = 1, к= п + 1.
. Нетрудно видеть, что первый индекс эле
мента верхней треугольной матрицы — это индекс строки /. Второй индекс определяется по выражению у = / + 1. Поэтому блок-схема алгоритма будет иметь вид, представленный на рис. 1.31. В алгоритме имеется два цикла: один внешний и второй внутренний. Такие циклы называются вложенными. Текстовая форма алгоритма приведена ниже.
Шаг 1. Ввести п, элементы матрицы А.
нали. Пусть задана исходная матрица А =
Согласно определению транспонированная к ней матрица
«з Ь = а31Ь1 + а32 Ь2 + т . Блок-схема алгоритма приведена на рис. 1.33. Текстовая форма дана ниже.
Шаг 1. Ввести п, т, элементы Ли Ь.
Шаг 4. Вычислить А* = 5* + а^Ьг
методом исключения Гаусса.
Суть метода Гаусса состоит в том, что сначала исключается первое неизвестное х, из всех уравнений, кроме первого. Затем исключается второе неизвестное х2 из всех уравнений, кроме первых двух. Последним исключается п — 1 неизвестное х„_, из последних двух уравнений. В результате получают систему уравнений треугольного вида
из которой сначала находят неизвестное хп = Ь’п1а’пп, затем методом подстановки значения хп в предшествующее уравнение очередное неизвестное потом
и заканчивают этот процесс вычислением значения
Таким образом, метод содержит два этапа: последовательное исключение неизвестных и последовательное их вычисление. Рассмотрим технику исключения неизвестных на примере трех уравнений с тремя неизвестными. Для этого систему уравнений
представим в матричном виде АХ = В, где А — матрица коэффи-
ры-столбцы неизвестных и правых частей уравнений. Далее рас
смотрим расширенную матрицу А’ =
В первом столбце матрицы А’ найдем наибольший по модулю, не равный нулю элемент. Если ненулевого элемента в столбце нет, рассмотренная система уравнений не имеет решений. Если наибольший ненулевой элемент содержится в любой строке матрицы А’, кроме первой, поменяем местами эту строку матрицы А’ с первой ее строкой. Этими действиями осуществляется контроль совместности системы уравнений и уменьшается чувствительность метода к округлению чисел, сопровождающему вычисления на ЭВМ.
Для того чтобы исключить первое неизвестное х, из второго уравнения системы, вычислим множитель т2 = а2х/ап, умножим первую строку матрицы А’ на этот множитель и вычтем результат умножения из второй строки А’.
из которой методом последовательной подстановки получим значения неизвестных
Обобщая изложенное, можно сказать, что алгоритм должен выполнить п — 1 действие по исключению п — 1 неизвестных. Если к — номер исключаемого переменного, то необходимо в каждом из этих действий сделать от / = к + 1 до п вычитаний уравнений. При этом каждое вычитание осуществляется выполнением у = к + 1 до п арифметических действий. Кроме этого, при каждом исключении переменной необходимо найти максимальный элемент в соответствующем столбце матрицы А. И последнее, что нужно сделать, вычислить значения неизвестных хп, . х,. Таким образом, общая укрупненная блок-схема алгоритма представляется такой (рис. 1.35).
Теперь составим алгоритмы поиска максимального элемента, вычитания строк и вычисления значений переменных, которые на этой схеме представлены укрупненными блоками.
Поиск индекса максимального элемента в ряду чисел рассмотрен в задаче 1.16. В данном случае он ничем не отличается от метода, который изложен там. Полагаем, что максимальный элемент первый в столбце Ли 1= к. Затем в цикле сравниваем с этим элементом остальные элементы этого столбца и тем самым выделяем наибольший элемент и устанавливаем его индекс. Алгоритм поиска минимального элемента в столбце матрицы А приведен на рис. 1.36. Там же показан фрагмент проверки условий совместности системы уравнений. На рис. 1.37 показана блок-схема алгоритма вычитания строк.
Алгоритм определения значений переменных хп, хп_х, . х, последовательно реализует формулы, по которым вычисляются эти переменные хп = Ьп/апп, хя_, = <Ьп_х — ап_ххп)/ап_х . Его блок-схема приведена на рис. 1.38. Ниже приведена текстовая форма полного алгоритма.
Шаг 3. Положить 1= к, / = к + 1.
Шаг 5. Положить / = / + 1, если / 1, вернуться к шагу 22. Шаг 28. Вывести х,, . л. и перейти к шагу 30.
Шаг 29. Вывести «Система несовместна».
Задача 1.29. Сконструировать алгоритм записи последовательности чисел 1, 2, 3, . 49 в квадратную матрицу А с 7 строками и 7 столбцами по спирали (рис. 1.39).
Рис. 1.39. Схема записи в матрицу А последовательности чисел
Самое простое решение этой задачи следующее. Двигаясь по спирали, составить две последовательности индексов элементов матрицы А. В первую последовательность занести значение индексов строк 1, 1, 1, 1, 1, 1, 1, 2, 3, 4, 5, 6, 7, 7, 7, 7, 7, 7, 7, 7, 7, 6, 5, 4, 3, 2, . во вторую последовательность — значения индексов столбцов 1, 2, 3, 4, 5, 6, 7, 7, 7, 7, 7, 7, 7, 7, 7, 6, 5, 4, 3, 2, 1, 1, 1, 1, 1, 1, 1, . . Затем организовать цикл от 1 до 49, в котором последовательно выбирать числа из двух последовательностей — индексы соответствующего элемента матрицы А и по этим индексам на место элемента матрицы а] заносить значение управляющей переменной цикла к.
Пусть / — строчные индексы матрицы А, у — индексы ее столбцов, к — управляющая переменная цикла. Пусть далее 4 — к-е значение строчного индекса, а ]к — к-е значение ее столбцевого индекса. С учетом этих обозначений алгоритм будет иметь вид, показанный на рис. 1.40.
Рис. 1.40. Алгоритм записи чисел натурального ряда 1, . 49 в матрицу А
Недостаток этого алгоритма заключается в том, что сначала необходимо составить последовательности индексов, отображающих движение по спирали, а затем программировать.
Можно предложить другой алгоритм, в котором записываются только начальные и конечные индексы сторон спирали. Например, для первых четырех ее сторон получим:
Для остальных двух спиралей индексы найдем аналогичным путем, исходя из рисунка спирали.
Таким образом, согласно этому подходу для записи в матрицу А чисел одной спирали требуется выполнить четыре цикла: два в прямом направлении и два в обратном. Чтобы ограничиться использованием только этих четырех циклов, необходимо найти, как изменятся индексы от номера спирали. Тогда алгоритм будет содержать один внешний и четыре внутренних цикла, начальные и конечные индексы которых зависят от индексов внешнего цикла. Доработку этого алгоритма мы выносим в качестве самостоятельного упражнения.
Задача 1.30. Рассмотрим шахматную доску и два положения коня на ней (рис. 1.41). Возможные ходы коня показаны стрелками и пронумерованы. Конь слева (поле (1,2)), не выходя за пределы доски, может пойти только на три поля. Конь справа (поле(5,6)) может пойти на восемь полей, что является макси-
- 2
- 4
- 6
- 8
мальным количеством допустимых ходов коня из одного ПОЛЯ. Маршрутом коня называется последовательное перемещение коня по полям доски такое, что он не попадает на одно и то же поле дважды. Конечной точкой маршрута является поле, с которого нет допустимого хода либо по причине выхода коня за пределы доски, либо по причине повторного попадания на какое-либо поле маршрута. Составить алгоритм, строящий маршрут коня, возможно наибольшей длины.
Очевидно, что наибольшая длина маршрута — это 63 поля шахматной доски. Попытаться найти такой маршрут можно путем перебора всех маршрутов коня, начинающихся из всех 64 полей. Поэтому, кроме процедуры построения маршрута, алгоритм должен содержать цикл из 64 повторений задания исходного поля.
Для того чтобы построить маршрут коня, начинающийся с любого поля доски, кроме учета ограничений, обеспечивающих допустимый ход, необходимо определить стратегию выбора очередного хода. Возможной такой стратегией может быть первый допустимый ход коня, если просматривать его ходы по часовой стрелке (см. 2-е положение коня, рис. 1.41). В том случае, когда допустимого хода нет, маршрут считается законченным.
В свою очередь, допустимость хода по условию непопадания на уже пройденное поле маршрута может быть определена так. Запишем во все поля доски значение нуль, а дальнейшие ходы коня с некоторого поля будем нумеровать числами, на которые конь делает очередной ход. Тогда допустимым полем будет поле доски со значением нуль, а максимальное число натурального ряда в конце маршрута определит его длину.
Выход коня за пределы доски может фиксироваться путем обрамления доски двумя полями, в которые записано произвольное число больше нуля, например 66. На рис. 1.42 приведены исходные данные о доске и показано начало маршрута коня из поля (7, 8).
На основании изложенного алгоритм поиска лучшего маршрута коня должен включать следующие этапы:
- 1) инициализацию полей обрамления доски, т. е. запись в эти поля числа 66 или любого другого, например 99;
- 2) инициализацию начала цикла по всем маршрутам с указанием начальной длины маршрута / = -1 для выбора лучшего маршрута;