Логарифм. Десятичный логарифм.
За основание логарифмов нередко берут цифру десять. Логарифмы чисел по основанию десять именуют десятичными. При проведении вычислений с десятичным логарифмом общепринято оперировать знаком lg, а не log; при этом число десять, определяющие основание, не указывают. Так, заменяем log10105 на упрощенное lg105; а log102 на lg2.
Для десятичных логарифмов типичны те же особенности, которые есть у логарифмов при основании, большем единицы. А именно, десятичные логарифмы характеризуются исключительно для положительных чисел. Десятичные логарифмы чисел, больших единицы, положительны, а чисел, меньших единицы, отрицательны; из двух не отрицательных чисел большему эквивалентен и больший десятичный логарифм и т. д. Дополнительно, десятичные логарифмы имеют отличительные черты и своеобразные признаки, которыми и поясняется, зачем в качестве основания логарифмов комфортно предпочитать именно цифру десять.
Перед тем как разобрать эти свойства, ознакомимся с нижеследующими формулировками.
Целая часть десятичного логарифма числа а именуется характеристикой, а дробная — мантиссой этого логарифма.
Характеристика десятичного логарифма числа а указывается как [lg а], а мантисса как
Возьмем, скажем, lg 2 ≈ 0,3010.Соответственно[lg 2] = 0,
Подобно и для lg 543,1 ≈2,7349. Соответственно,[lg 543,1] = 2,
Достаточно повсеместно употребляется вычисление десятичных логарифмов положительных чисел по таблицам.
Характерные признаки десятичных логарифмов.
Первый признак десятичного логарифма. Десятичный логарифм целого не отрицательного числа, представленного единицей со следующими нулями, есть целое положительное число, равное численности нулей в записи выбранного числа.
Возьмем, lg 100 = 2, lg 1 00000 = 5.
То а= 10 n , из чего получаем
Второй признак. Десятичный логарифм положительной десятичной дроби, показанный единицей с предыдущими нулями, равен — п, где п — численность нулей в представлении этого числа, учитывая и нуль целых.
Рассмотрим, lg 0,001 = — 3, lg 0,000001 =-6.
,
То a= 10 -n и получается
Третий признак. Характеристика десятичного логарифма не отрицательного числа, большего единицы, равна численности цифр в целой части этого числа исключая одну.
Разберем данный признак 1) Характеристика логарифма lg 75,631 приравнена к 1.
lg 10 n -1 lgа n .,
n-1 n ,то десятичный логарифм его возрастет на п.
Действительно, по формуле логарифма произведения
lg (739,15 •100) = lg 739,15 + 2;
Перемещение запятой в положительной десятичной дроби на п знаков вправо равноценно операции перемножения заданной дроби с 10 n . Следовательно, при перемещении запятой в положительной десятичной дроби на п знаков вправо десятичный логарифм возрастет на п.
Шестой признак. Если поделить число на 10 n , то десятичный логарифм уменьшается на п.
При перемещении запятой в положительной десятичной дроби на п знаков влево десятичный логарифм уменьшается на п.
Например, lg 0,3567 = lg 35,67 -2;lg 0,00054 = lg 0,54 -3.
Все обоснованные ранее признаки десятичных логарифмов касались их характеристики. Далее разберем признаки мантиссы десятичных логарифмов.
Седьмой признак десятичного логарифма. Мантисса десятичного логарифма положительного числа не меняется, если умножить это число на 10 n с заданным целым показателем п.
Обоснованно, что при заданном целом п (как положительном, так и отрицательном)
Но дробная часть числа не меняется при прибавлении к нему целого числа.
Смещение запятой в десятичной дроби вправо или влево равнозначно операции перемножения этой дроби на степень числа десять с целым показателем п (положительным или отрицательным). И следовательно, при смещении запятой в положительной десятичной дроби влево или вправо мантисса десятичного логарифма этой дроби не меняется.
Источник статьи: http://www.calc.ru/Desyatichniy-Logarifm.html
Десятичный логарифм
Определение. Логарифмом числа b по основанию a , где a > 0 , a ≠ 1 , b > 0 , называется показатель степени, в которую нужно возвести основание a , чтоб получить число b .
Определение. Десятичный логарифм — логарифм по основанию 10.
Другими словами, десятичный логарифм числа b является решением уравнения 10 x = b .
Обозначение. Десятичный логарифм обозначается lg x или log x .
Калькулятор десятичных логарифмов
Свойства десятичного логарифмов
lg x = log10 x — так как основание десятичного логарифма равно 10.
Доказать равенство: a lg b = b lg a .
Запишем очевидное равенство:
Возведем 10 в соответствующие степени
10 lg b · lg a = 10 lg a · lg b
(10 lg b ) lg a = (10 lg a ) lg b
Зная, что lg 2 = a , lg 3 = b , lg 5 = c , выразить lg 6; lg 30; lg 16 через a, b, c.
Используем формулы логарифма произведения и степени получим:
lg 6 = lg (2·3)= lg 2 + lg 3 = a + b ;
lg 30 = lg (5·2·3)= lg 5 + lg 2 + lg 3 = a + b + c ;
lg 16 = lg 2 4 = 4 · lg 2 = 4 a .
Вычислить log9 5 · log25 27.
log9 5 · log25 27 = lg 5 lg 9 · lg 27 lg 25
Используем свойство логарифма степени lg x n = n lg x :
lg 5 lg 9 · lg 27 lg 25 = lg 5 lg 3 2 · lg 3 3 lg 5 2 = lg 5 2 lg 3 · 3 lg 3 2 lg 5 = 3 4
Вычислить log30 8, если lg 5 = a , lg 3 = b .
log 30 8 = lg 8 lg 30 = lg 2 3 lg (3 · 10) =
Используем свойство логарифма степени, произведения, частного и то что 2= 10 5 :
= 3 lg 2 lg 3 + lg 10 = 3 lg 2 lg 3 + 1 = 3 lg 10 5 lg 3 + 1 = 3(lg 10 — lg 5) lg 3 + 1 = 3(1 — lg 5) lg 3 + 1 =
Подставим lg 5 = a , lg 3 = b :
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Источник статьи: http://ru.onlinemschool.com/math/library/log/common_logarithm/
Десятичный логарифм числа
Результатом вычисления логарифма числа является показатель степени, в которую необходимо возвести одно число для получения другого.
Определение десятичного логарифма
Десятичный логарифм — это логарифм, основанием которого является число 10. Обозначается как lg и пишется следующим образом:
lg y является решением уравнения y = 10 x . Другими словами, в какую степень ( x ) необходимо возвести число 10, чтобы получить y .
Связь с натуральным логарифмом
Данное соотношение получено путем перехода к новому основанию:
Свойства десятичного логарифма
| Свойств | Формула | Пример |
| Логарифм умножения | lg (10 ⋅ 100) = lg 10 + lg 100 | |
| Логарифм деления | lg (100 / 10) = lg 100 — lg 10 | |
| Логарифм степени | lg 10 3 = 3 ⋅ lg 10 | |
| Логарифм корня | » data-order=» | » data-order=» |
| Производная логарифма | » data-order=» | |
| Интеграл логарифма | » data-order=» | |
| Логарифм бесконечности | » data-order=» | |
| Логарифм отрицательного числа | Логарифм числа 0 | lg 0 не определен |
| Логарифм числа 1 | lg 1 = 0 | |
| Логарифм числа 10 | lg 10 = 1 |
Таблица десятичных логарифмов
| 1 | 0 | 26 | 1,41497 | 51 | 1,70757 | 76 | 1,88081 |
| 2 | 0,30103 | 27 | 1,43136 | 52 | 1,716 | 77 | 1,88649 |
| 3 | 0,47712 | 28 | 1,44716 | 53 | 1,72428 | 78 | 1,89209 |
| 4 | 0,60206 | 29 | 1,4624 | 54 | 1,73239 | 79 | 1,89763 |
| 5 | 0,69897 | 30 | 1,47712 | 55 | 1,74036 | 80 | 1,90309 |
| 6 | 0,77815 | 31 | 1,49136 | 56 | 1,74819 | 81 | 1,90849 |
| 7 | 0,8451 | 32 | 1,50515 | 57 | 1,75587 | 82 | 1,91381 |
| 8 | 0,90309 | 33 | 1,51851 | 58 | 1,76343 | 83 | 1,91908 |
| 9 | 0,95424 | 34 | 1,53148 | 59 | 1,77085 | 84 | 1,92428 |
| 10 | 1 | 35 | 1,54407 | 60 | 1,77815 | 85 | 1,92942 |
| 11 | 1,04139 | 36 | 1,5563 | 61 | 1,78533 | 86 | 1,9345 |
| 12 | 1,07918 | 37 | 1,5682 | 62 | 1,79239 | 87 | 1,93952 |
| 13 | 1,11394 | 38 | 1,57978 | 63 | 1,79934 | 88 | 1,94448 |
| 14 | 1,14613 | 39 | 1,59106 | 64 | 1,80618 | 89 | 1,94939 |
| 15 | 1,17609 | 40 | 1,60206 | 65 | 1,81291 | 90 | 1,95424 |
| 16 | 1,20412 | 41 | 1,61278 | 66 | 1,81954 | 91 | 1,95904 |
| 17 | 1,23045 | 42 | 1,62325 | 67 | 1,82607 | 92 | 1,96379 |
| 18 | 1,25527 | 43 | 1,63347 | 68 | 1,83251 | 93 | 1,96848 |
| 19 | 1,27875 | 44 | 1,64345 | 69 | 1,83885 | 94 | 1,97313 |
| 20 | 1,30103 | 45 | 1,65321 | 70 | 1,8451 | 95 | 1,97772 |
| 21 | 1,32222 | 46 | 1,66276 | 71 | 1,85126 | 96 | 1,98227 |
| 22 | 1,34242 | 47 | 1,6721 | 72 | 1,85733 | 97 | 1,98677 |
| 23 | 1,36173 | 48 | 1,68124 | 73 | 1,86332 | 98 | 1,99123 |
| 24 | 1,38021 | 49 | 1,6902 | 74 | 1,86923 | 99 | 1,99564 |
| 25 | 1,39794 | 50 | 1,69897 | 75 | 1,87506 | 100 | 2 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 10 | 100 | 1000 | 10000 | 100000 | 1000000 | 10000000 | 100000000 | 1000000000 | 10000000000 |
График десятичного логарифма
Функция десятичного логарифма задается как y = lg x . Существует только при неотрицательных значениях переменной x. График выглядит так:
Источник статьи: http://microexcel.ru/desyatichny-logarifm/


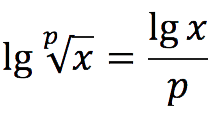 «>
«>  «>
«>  » data-colspan=»2″ data-rowspan=»1″>
» data-colspan=»2″ data-rowspan=»1″>  » data-colspan=»2″ data-rowspan=»1″>
» data-colspan=»2″ data-rowspan=»1″>  » data-colspan=»2″ data-rowspan=»1″>
» data-colspan=»2″ data-rowspan=»1″>