Самое большое число в мире, которое что-то обозначает
Число Грэма — самое большое число в мире, которое что-то обозначает. Это не единица с огромным количеством нулей. Мы не можем его себе представить. Но давайте по порядку.
Миллион — 1.000.000. Обозначается как 10 в 6 степени. Мы легко можем представить миллион чего-то: миллион рублей, миллион долларов и т.п..
Миллиард — 1.000.000.000 или тысяча миллионов. Обозначается 10 в 9 степени. Представить миллиард чего-то мы тоже можем: 7 миллиардов человек живёт на нашей планете, 100 миллиардов звёзд в млечном пути.
Триллион — 1.000.000.000.000. Обозначается 10 в 12 степени. Триллион рыб живёт в мировом океане.
Квадриллион — 1.000.000.000.000.000. Обозначается 10 в 15 степени. Квадриллион муравьёв живёт на нашей планете.
Квинтиллион — 1.000.000.000.000.000.000. Обозначается 10 в 18 степени. Именно столько кубометров воды есть на земле.
Но это только начало!
Секстиллион — 1.000.000.000.000.000.000.000. Обозначается 10 в 21 степени. Около секстиллиона звёзд мы можем наблюдать в видимой части космоса. Её называют сферой Хаббла. Статья о ней скоро появится (уже появилась) на канале.
Септиллион — 1.000.000.000.000.000.000.000.000. Обозначается 10 в 24 степени. Наша планета весит септиллион килограммов или секстиллион тонн.
Квинквавигинтиллион — 10 в 78 степени. Сто квинквавигинтиллионов — количество субатомных частиц в видимой вселенной.
Гугол — 10 в степени 100. Существует теория, что через гугол лет последняя чёрная дыра взорвётся и вселенная сожмётся до первоначального состояния. Также существует число гуголплекс — 10 в степени гугол, гуголплексплекс — 10 в степени гуголплекс и так далее, но у этих чисел нет никакого значения. Это просто цифры.
10 в 185 степени — объём видимой вселенной с точки зрения планковских величин. Это наиболее маленький объём, который человек может представить и вычислить. Планковская длина приблизительно равна 1,616229(38) умножить на 10 в -35 степени метров.
10 в 500 степени — число возможных вселенных, если верить теории струн. Если хотите статью о ней — пишите в комментарии.
Числа Марсенна. Самое большое из них — 2 в степени 43.112.609 -1 (сорок три миллиона сто двенадцать тысяч шестьсот девять) — самое большое простое число, которое делится только на себя и на 1. Его длина — почти 13.000.000 цифр.
Число Скьюза. Записывается как 10 в степени 10 в степени 10 в степени 963. Обозначает верхний предел для математической задачи.
И вот наконец — число Грэма. Обозначает верхнюю границу решений задач с гиперкубом. Вспомним стрелочную нотацию Кнута, которая используется для обозначения больших числовых совокупностей. Суть метода состоит в добавлении вертикальных стрелок, вместо ступенчатых степеней. Вертикальную стрелку будем обозначать символом «|» Например 3|3=3 в степени 3 и равняется 27. 3||3=3 в степени 3 в степени 3 или 3 в степени 27 и равняется 7.625.597.484.987.
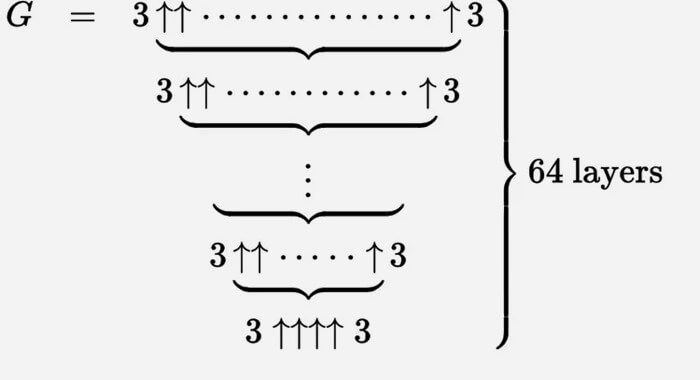
3|||3 это 3 с высотой столба степени 3 равной расстоянию от Земли до Марса. Количество троек в степени равняется 7.000.000.000.000. И заметьте, это не само число, а его степень! Математики обозначили его G1. Всего 5 троек из этой башни полностью покрывают гуголплекс, а первые 10 сантиметров ставят в тупик все существующие на Земле компьютеры. Дальше пустота и неведение. Далее идёт число G2, где количество стрелок равняется G1. Далее идёт G3, где количество стрелок равняется G2 и так далее. Всего таких чисел 64. G64 это и есть число Грэма. Записать его где либо невозможно, поэтому записывают формулой: G=f^64(4), где f(n)=3|^n3. (значок «^» обозначает степень: 1.000.000=10^6). Подсчитывать это бессмысленно. Число Грэма не поместится в тех самых 10 в степени 500 вселенных, даже если пронумеровать каждую частицу! Но мы всё же кое что знаем о нём. Вот последние 10 цифр этого числа: 2464195387. Первые цифры не знает никто. Возможно, через тысячи или десятки тысяч лет человечество всё-таки сможет его высчитать и оно станет элементарным и банальным.
Подписывайтесь на канал ставьте лайки, делитесь своим мнение в комментариях.
Источник статьи: http://zen.yandex.ru/media/id/5bd804fea6560100aaad6444/samoe-bolshoe-chislo-v-mire-kotoroe-chtoto-oboznachaet-5c5d4c0a2e6eb000ad30fd42
Как писать числа в текстах? Несколько правил
Без чисел в любом тексте никуда. Даже в самом маленьком. Поэтому определённые правила написания есть и для них. Давайте разбираться, как их писать.
1. Если говорим о крупных суммах чего-либо, то лучше записывать в буквенно-цифровом виде: 50 тыс. руб., 100 млн руб . Так проще будет прочитать, чем запись вроде «100 000 000 руб».
2. Физические величины или суммы денег тоже нужно писать цифрами: 6 кг, 220 В, 350 км.
3. Если надо записать большое число, то делать это нужно по три цифры, то есть в соответствии с разрядами: тысячами, миллионами.
Однако в обозначениях нормативных документов числа на группы цифр не разбиваются. Закон № 3241.
4. После «тыс» (тысяч) ставится точка, после «млн» и «млрд» — нет.
7 тыс. 9 млн, 152 млрд
Такое смешанное написание применяется для крупных круглых чисел от 1 000.
5. В начале предложения используется словесная форма записи.
Тысяча человек положительно оценила эту реформу.
Это правило не касается заголовков. Если вы пишете о большом количестве, то нужно перестроить предложение так, чтобы число писалось в середине или конце.
В России живёт 146 780 720 человек, если верить «Википедии».
6. Также словесная форма необходима, когда идут подряд несколько чисел:
Мы хотим забронировать два 4-местных номера.
7. Окончания используются только у порядковых числительных. 7-е место, 14-го дома . К числам через дефис добавляется одна буква, когда перед ней стоит гласная ( 9-й ), и две буквы, если предшествует согласная ( 9-го ). А также: 90-е, 90-х, 70-е, 70-х .
8. В количественных числительных окончания не ставятся: более 2 лет, не более 3 человек в очереди . То же самое касается сложных слов: 2-местный (двухместный), 5-летний (пятилетний), 4-секционный (четырёхсекционный), 1-комнатный (однокомнатный).
Если статья была для вас полезной, ставьте лайк и подписывайтесь на канал. 🙂 Тому, кто зашёл на канал впервые, сообщаю, что здесь вы найдёте много интересных публикаций о русском языке, полезных книгах и ресурсах для улучшения своей грамотности.
Источник статьи: http://zen.yandex.ru/media/gramotnost/kak-pisat-chisla-v-tekstah-neskolko-pravil-5de613b9bc251400af6bf6bf
Самое большое число в мире
Считается, что концепция чисел впервые возникла, когда доисторические люди начали использовать свои пальцы для подсчета чего-либо. С тех пор человечество прошло долгий путь. Теперь мы используем калькуляторы и компьютеры для подсчета самых больших чисел. И даже появились названия для чисел, которые настолько велики, что их с трудом можно представить.
Бесконечность счетных чисел
Казалось бы, ответ на вопрос о том, каково самое большое число в математике — очень прост. Бесконечность, верно? Но это не совсем правильно. Ведь бесконечность — вовсе не число, а концепция. Идея.
Бесконечность (infinitum) — это понятие, которое в переводе с латинского означает «без границ». Определение бесконечности в математике гласит, что независимо от того, насколько велико число, вы всегда можете добавить к нему 1, и оно станет больше.
Поэтому, строго говоря, не существует такого понятия, как самое большое число в мире. Можно лишь назвать наибольшее число, которому дали конкретное название.
Вот некоторые наиболее известные названия больших чисел:
| Число нулей | Название | Название на английском |
|---|---|---|
| 3 | тясяча | thousand |
| 6 | миллион | million |
| 9 | миллиард (биллион) | billion |
| 12 | триллион | trillion |
| 15 | квадриллион | quadrillion |
| 18 | квинтиллион | quintillion |
| 21 | секстиллион | sextillion |
| 24 | септиллион | septillion |
| 27 | октиллион | octillion |
| 30 | нониллион | nonillion |
| 33 | дециллион | decillion |
| 36 | ундециллион | undecillion |
| 39 | дуодециллион | duodecillion |
| 42 | тредециллион | tredecillion |
| 45 | кватуордециллион | quattuordecillion |
| 48 | квиндециллион | quindecillion |
| 51 | сексдециллион | sexdecillion |
| 54 | септендециллион | septendecillion |
| 57 | октодециллион | octodecillion |
| 60 | новемдециллион | novemdecillion |
| 63 | вигинтиллион | vigintillion |
| 66 | унвигинтиллион | unvigintillion |
| 69 | дуовигинтиллион | duovigintillion |
| 72 | тревигинтиллион | trevigintillion |
| 75 | кватуорвигинтиллион | quattuorvigintillion |
| 78 | квинвигинтиллион | quinvigintillion |
| 81 | сексвигинтиллион | sexvigintillion |
| 84 | септенвигинтиллион | septenvigintillion |
| 87 | октовигинтиллион | octovigintillion |
| 90 | новемвигинтиллион | novemvigintillion |
| 93 | тригинтиллион | trigintillion |
| 96 | унтригинтиллион | untrigintillion |
| 99 | дуотригинтиллион | duotrigintillion |
| 102 | третригинтиллион | trestrigintillion |
| 105 | кватортригинтиллион | quattuortrigintillion |
| 108 | квинтригинтиллион | quintrigintillion |
| 111 | секстригинтиллион | sextrigintillion |
| 114 | септентригинтиллион | septentrigintillion |
| 117 | октотригинтиллион | octotrigintillion |
| 120 | новемтригинтиллион | novemtrigintillion |
| 123 | квадрагинтиллион | quadragintillion |
| 126 | унквадрагинтиллион | unquadragintillion |
| 129 | дуоквадрагинтиллион | duoquadragintillion |
| 132 | треквадрагинтиллион | trequadragintillion |
| 135 | кваторквадрагинтиллион | quattuorquadragintillion |
| 138 | квинквадрагинтиллион | quinquadragintillion |
| 141 | сексквадрагинтиллион | sexquadragintillion |
| 144 | септенквадрагинтиллион | septenquadragintillion |
| 147 | октоквадрагинтиллион | octoquadragintillion |
| 150 | новемквадрагинтиллион | novemquadragintillion |
| 153 | квинквагинтиллион | quinquagintillion |
| 156 | унквинкагинтиллион | unquinquagintillion |
| 159 | дуоквинкагинтиллион | duoquinquagintillion |
| 162 | треквинкагинтиллион | trequinquagintillion |
| 165 | кваторквинкагинтиллион | quattuorquinquagintillion |
| 168 | квинквинкагинтиллион | quinquinquagintillion |
| 171 | сексквинкагинтиллион | sexquinquagintillion |
| 174 | септенквинкагинтиллион | septenquinquagintillion |
| 177 | октоквинкагинтиллион | octoquinquagintillion |
| 180 | новемквинкагинтиллион | novemquinquagintillion |
| 183 | сексагинтиллион | sexagintillion |
| 186 | унсексагинтиллион | unsexagintillion |
| 189 | дуосексагинтиллион | duosexagintillion |
| 192 | тресексагинтиллион | tresexagintillion |
| 195 | кваторсексагинтиллион | quattuorsexagintillion |
| 198 | квинсексагинтиллион | quinsexagintillion |
| 201 | секссексагинтиллион | sexsexagintillion |
| 204 | септенсексагинтиллион | septensexagintillion |
| 207 | октосексагинтиллион | octosexagintillion |
| 210 | новемсексагинтиллион | novemsexagintillion |
| 213 | септагинтиллион | septuagintillion |
| 216 | унсептагинтиллион | unseptuagintillion |
| 219 | дуосептагинтиллион | duoseptuagintillion |
| 222 | тресептагинтиллион | treseptuagintillion |
| 225 | кваторсептагинтиллион | quattuorseptuagintillion |
| 228 | квинсептагинтиллион | quinseptuagintillion |
| 231 | секссептагинтиллион | sexseptuagintillion |
| 234 | септенсептагинтиллион | septenseptuagintillion |
| 237 | октосептагинтиллион | octoseptuagintillion |
| 240 | новемсептагинтиллион | novemseptuagintillion |
| 243 | октогинтиллион | octogintillion |
| 246 | уноктогинтиллион | unoctogintillion |
| 249 | дуооктогинтиллион | duooctogintillion |
| 252 | треоктогинтиллион | treoctogintillion |
| 255 | кватороктогинтиллион | quattuoroctogintillion |
| 258 | квиноктогинтиллион | quinoctogintillion |
| 261 | сексоктогинтиллион | sexoctogintillion |
| 264 | септоктогинтиллион | septoctogintillion |
| 267 | октооктогинтиллион | octooctogintillion |
| 270 | новемоктогинтиллион | novemoctogintillion |
| 273 | нонагинтиллион | nonagintillion |
| 276 | уннонагинтиллион | unnonagintillion |
| 279 | дуононагинтиллион | duononagintillion |
| 282 | тренонагинтиллион | trenonagintillion |
| 285 | кваторнонагинтиллион | quattuornonagintillion |
| 288 | квиннонагинтиллион | quinnonagintillion |
| 291 | секснонагинтиллион | sexnonagintillion |
| 294 | септеннонагинтиллион | septennonagintillion |
| 297 | октононагинтиллион | octononagintillion |
| 300 | новемнонагинтиллион | novemnonagintillion |
| 303 | центиллион | centillion |
Как называется самое большое простое число
Простое число — то, которое делится только на себя и на единицу. В конце 2018 года американец Патрик Лярош представил научному миру самое большое простое число.
- Длина его — 24 862 048 символов. Для сравнения: в эпохальном произведении Л.Н. Толстого «Война и мир» около 6-7 миллионов символов, если учитывать знаки препинания и пробелы.
- Это число можно записать следующим образом: 2 82589933 -1
- А читается оно так: два в степени 82589933 минус один.
- Существует целый онлайн-проект GIMPS, нацеленный как раз на поиск самых больших простых чисел. В нем принимают участие математики из разных стран. Поэтому новые рекордсмены появляются часто. Работают ученые, что называется, не за страх, а за деньги. Ведь тому, кто откроет следующее наибольшее простое число Мерсенна достанется 3000 долларов.
Какое самое большое число в мире
В 1980 году в Книгу рекордов Гиннеса вошло число Грэма (оно же G64 или G), названное в честь американского математика Рональда Грэма. Оно является наибольшим числом, которое когда-либо использовалось в важном математическом доказательстве. Речь идет про теорию Франка Рамсея.
Кратко об этой теории: представим себе N-мерный куб, его вершины в случайном порядке соединены красными или синими отрезками-линиями. А наша задача — понять, до какого значения N возможно (если по-разному закрашивать ребра куба), избежать ситуации, при которой одна плоскость в кубе будет окрашена одним цветом. То есть у нас не должен получиться одноцветный «конвертик».
Математики позакрашивали кубик и так и эдак, получилось, что до шестимерного куба можно исхитриться и сделать, чтобы линии одного цвета, соединяющие четыре вершины, не лежали в одной плоскости. А вот с семимерным, как выяснили Грэм и Ротшильд, такой фокус уже не провернешь. И с восьмимерным. И… «и так далее», которое, впрочем, не бесконечно, а заканчивается фантастически гигантским числом. Вот его-то и именуют числом Грэма. Кстати, в настоящее время решение Грэма и Ротшильда устарело. Математики выяснили, что 6-7-8-9-10-11-12-мерные кубы все же можно покрасить без «конвертов». Но где-то в промежутке между 13 и числом Грэма гарантированно есть число выше которого «конверты» в любом случае будут.
Число Грэма получило всемирное признание в 1977 году, когда известный популяризатор науки Мартин Гарднер написал об этом в Scientific American.
И хотя с тех пор в математической науке были и другие кандидаты на титул самого большого числа, «детище» Грэма является самым распиаренным и общеизвестным. И если вы слышали про «гугольное семейство»:
- гугол — 10 100 ;
Или: 10 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 - гуголплекс — 10 гугол ,
то знайте, что этими числами в математике лишь «разминаются», а число Грэма в немыслимое количество раз больше, чем они. И даже больше, чем число Скьюза, находящееся между 10 19 и 1,3971672·10 316 и приблизительно равное e 727,951336108 .
Любопытно, что придумав гугол американский математик Эдвард Казнер хотел показать студентам разницу между невероятно большим числом и бесконечностью. Тогда число Грэма может просто «взорвать мозг».
Возможно ли представить и записать число за гранью понимания
Математики не смогут назвать вам точное количество цифр в числе Грэма, не говоря уже о том, чтобы досчитать до него. Известны лишь последние 50 цифр самого большого числа в мире — это …03222348723967018485186439059104575627262464195387.
А вот цифры, с которых начинается G64 неизвестны, и вряд ли когда-либо будут.
Давайте сравним трех монстров: гугол, гуголплекс и число Грэма.
- Гугол — это количество песчинок, которые могут поместиться во вселенной, умноженное на 10 миллиардов. Итак, представьте себе вселенную, заполненную мелкими песчинками — на десятки миллиардов световых лет над Землей, под ней, перед ней, позади нее — бесконечный песок.
Теперь представьте, что в какой-то момент вы берете одну песчинку, чтобы рассмотреть ее под мощным микроскопом. И видите, что на самом деле это не единственное зерно, а 10 миллиардов микроскопических зерен, а все вместе они размером с песчинку. Если бы это было так для каждой отдельной песчинки в этой гипотетической вселенной, то общее количество этих микроскопических зерен было бы гуголом.
- Для количественной оценки гуголплекса астроном и астрофизик Карл Саган привел пример заполнения всего объема наблюдаемой вселенной мелкими частицами пыли размером приблизительно 1,5 микрометра. Исходя из этого, общее количество различных комбинаций, в которых эти частицы могут быть расположены, будет равно примерно одному гуголплексу.
- А теперь представим, что гуголплекс — это даже не песчинка, а крохотная точка, которую можно рассмотреть лишь в самый мощный микроскоп. И у нас вся вселенная заполнена такими крохотными точками. Так вот, даже это не идет ни в какое сравнение с числом Грэма. Но что, если мы хотим использовать все пространство наблюдаемой вселенной для его записи (предположим, что запись каждой цифры занимает как минимум объём Планка)? Увы, у нас это не выйдет! Но всегда можно пойти другим путем.
Как записать G64 с помощью метода Кнута
В 1976 году американский ученый Дональд Кнут предложил понятие сверхстепеней или нотацию Кнута. Это метод, позволяющий при помощи стрелочек, направленных вверх, записывать очень большие числа. Возведение в степень обозначается одной стрелкой вверх: ↑.
Вот как выглядит эта нотация: a ↑ b = ab = a × a × a × …, и так b раз.
- Например 3↑3 = 3³.
- Гугол записывается так 10↑10↑2.
- А гуголплекс — 10↑10↑10↑2
Важной особенностью стрелок вверх является то, что они растут очень быстро. Экспонентация растет гораздо быстрее, чем умножение. 2 × 10 — это всего лишь 20, но 2↑10 = 1024. Таким же образом, каждый новый уровень стрелок растет намного быстрее, чем предыдущий уровень.
Если мысленно представить себе степенную башню из троек 3↑↑↑4 то получится конструкция, размером от Земли до Марса. А ведь мы еще даже не дошли до «нижней ступеньки», ведущей нас к числу Грэма.
Мы можем описать число Грэма огромным набором этих стрелок вверх.
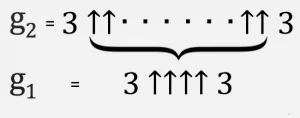
Проще всего думать об этом как об итерационном процессе. Мы начинаем снизу с g 1 = 3 ↑↑↑↑ 3, а затем создаем вторую строку (назовем ее g 2) с g 1 стрелками между тройками.
Тогда g 3 — это две тройки, разделенные g 2 стрелками вверх и так далее, пока g 64 с g 63 стрелками между тройками не будет числом Грэма.
Если выбрать продолжительность жизни, равную числу Грэма вместо бессмертия, то результат будет практически одинаков. Даже если предположить, что условия во Вселенной, в Солнечной системе и на Земле вечно останутся неизменными, человеческий мозг никак не мог бы выдержать столь длинный промежуток времени без пагубных изменений.
Источник статьи: http://basetop.ru/samoe-bolshoe-chislo-v-mire/