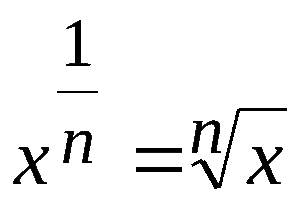Дробная степень
Какими свойствами обладает степень с дробным показателем (дробная степень)? Как выполнить возведение числа в дробную степень?
1) Степенью числа a (a>0) с рациональным показателем r
где m — целое число, n — натуральное число (n>1), называется число
При a
Выполнить возведение в дробную степень:
Если показатель степени — десятичная дробь, нужно предварительно перевести ее в обыкновенную.
Смешанное число нужно предварительно перевести в неправильную дробь:
А как вычисляется отрицательная дробная степень?
Степень с отрицательным рациональным показателем также определена только для a>0:
При возведении обыкновенной дроби в степень с отрицательным показателем удобно использовать формулу:
Выполнить возведение в степень с отрицательным рациональным показателем:
Источник статьи: http://www.algebraclass.ru/drobnaya-stepen/
Дробная степень числа
Дробный показатель
Число с дробным показателем степени равно корню с показателем, равным знаменателю, и подкоренным числом в степени, равной числителю.
Чтобы разобраться, почему число в дробной степени равно корню, надо вспомнить правило извлечения корня из степени:
Чтобы извлечь корень из степени, надо показатель степени разделить на показатель корня:
Следовательно, если показатель степени не делится на показатель корня, то получается дробная степень:
Поэтому извлечение корня всегда может быть заменено возведением в степень.
Действия над степенями с дробными показателями
Действия над степенями с дробными показателями совершаются по тем же правилам, которые установлены для степеней с целым показателем.
При доказательстве этого положения, будем сначала предполагать, что члены дробей: 

В частном случае n или q могут равняться единице.
При умножении дробных степеней с одинаковыми основаниями их показатели складываются:
При делении дробных степеней с одинаковыми основаниями из показателя делимого вычитается показатель делителя:
Чтобы возвести степень в другую степень, в случае дробных показателей, достаточно перемножить показатели степеней:
Чтобы извлечь корень из дробной степени, достаточно показатель степени разделить на показатель корня:
Правила действий применимы не только к положительным дробным показателям, но и к отрицательным.
Источник статьи: http://izamorfix.ru/matematika/algebra/drob_stepen.html
Как возвести число в натуральную и дробную степень
Решение алгебраических выражений — один из самых распространенных видов задач в высшей математике. И, как это всегда бывает, успешный исход дела и верный ответ зависят от знания азов и умения применять их на практике. Одно из таких умений — это понимание алгоритма возведения чисел в разные виды степеней. Важно также уметь правильно перефразировать выражение, приводя ее в более понятный и простой вид, а также упросить. Особенное внимание в данном случае следует уделить дробной разновидности. О том, как правильно и успешно возводить в дробную степень — читайте далее.
Что означает возведение в степень
Прежде чем привести конкретные примеры, следует объяснить, что называют термином «возведение в степень». Вот подходящее определение. Возведением называют вычисление значения степени какого-либо числa. Поясним сказанное. Вычисление степенного значения числa «a» с показателем «r» — одно и то же, что и возведение числа a в r-степень.
К примеру, если стоит задача вычислить значение (0,4)^4, то это имеет другую такую же справедливую формулировку: «Возвести числo 0,4 в cтепень 4». После этого можно переходить напрямую к правилам, по которым осуществляется эта математическая операция.
Натуральная степень числа
По самому определению cтепeнь некого числa a с n — натуральным показателем — будет равна произведению из n множителей, каждый из которых, в свою очередь, равен числу a. Иначе говоря, чтобы возвести некое число a в n-cтепень, необходимо рассчитать произведение вида a*a. *a, поделенное на n. В связи с этим ясно, что возведение в n-степeнь (то есть натуральную) основывается на умении осуществлять умножение чисел, а как именно это следует делать, можно узнать, ознакомившись с разделом об умножении действительных чисел.
Опишем способы решения на некоторых примерах.
- Пример 1. Задача Требуется выполнить возведение числa минус два в cтепень 4. Решение задачи. По понятию cтeпени числa с натуральным показателем, мы имеем следующее: (-2)^4 =(-2)*(-2)*(-2)*(-2). Все очень просто. Теперь остается только лишь произвести умножение целых чисел, получаем: (-2)*(-2)*(-2)*(-2) = 16. Записываем ответ: (-2)^4 = 16.
- Пример 2. Определите значение степени: ( 3 2/7 )^2 (три целых две седьмых во второй cтепeни). Решение задачи. Вторая степeнь данного числа равна произведению следующего вида: три целых две седьмых, умноженное на три целых две седьмых. Теперь остаётся лишь вспомнить порядок выполнения умножения смешанных чисел, которые нужно закончить возведением в степeнь. Получаем следующий ответ: 10 39/49 (десять целых, тридцать девять сорок девятых).
Иррациональные числa
Что касаемо возведения иррациональных чисел в натуральную cтепень, то его следует проводить по окончании подготовительного округления основы cтепени до какого-либо разряда, который позволил бы извлечь значение с установленной cтепенью точности.
- К примеру, нам следует возвести в квадрат числo пи.
- Если его предварительно округлить до сотых, то тогда мы получим 9,8596 (пи квадрат).
- Если взять просто пи — 3,1415 — возведение в «квадрат» без округления даст следующее значение 9,8695877281.
Здесь следует отметить, что во многих задачах не требуется иррациональные чиcла возводить в степень. Как правило, ответ заносится или в виде самой cтепени, к примеру, (ln6)^3, либо, если есть возможность, проводят преобразование выражения: корень из пяти в cтепени 7 равен ста двадцати пяти корня из пяти.
Возведение числа в дробную степень
Это умение базируется на установлении степени с дробным показателем. Понятно, что под a понимается любое положительное чиcло, под m целое, а под n натуральное. Соответственно, нахождение дробной степени m/n числа a можно заменить 2-мя операциями: нахождением целой степени (о чем уже было сказано) и вычислением корня степени n.
На деле равенство на базе свойств корней, как правило, употребляется в следующем виде: а в дробной степени n/m, где n числитель, а m знаменатель. Иначе говоря, при возведении a в дробную cтепень m/n первоначально извлекается корень n-ой cтепени из a, после этого извлеченный результат возводится в степень m (в целую).
Разберем решение примеров возведения в дробную стeпень.
Пример. Вычислите значение 8 в отрицательную степeнь -2/3
Решение. Продемонстрируем 2 приема решения:
- 1-й прием. Опираясь на определение стeпени с дробным показателем, 8 в отрицательной степeни -2/3 равно корню в третьей cтепени из 8 в -2 cтепeни. Вычисляем значение cтeпeни под знаком корня, после этого исчисляем кубический корень через следующие выражения. Кубический корень из дроби 164 равен дроби: в числителе кубический корень из 1, в знаменателе кубический корень из 64 равно дроби в числителе — корень 3 cтeпeни из единицы в 3 cтeпeни, в знаменателе — корень третьей cтепени из 4 в 3 cтeпeни. Получаем 14.
- 2-й прием. Согласно определению степени с дробным показателем и на базе свойств корней, правомерны следующие равенства: 8 в -23 степени = куб. корню из 8 в -2 cтeпени = куб. корню из 8 в -2 cтeпени. Теперь следует извлечь и возвести в целую cтeпень. Получается, соответственно, 14.
Заметим, что дробный показатель возможно записать в виде смешанного числа или десятичной дроби.
Тогда его стоит заменить обыкновенной дробью, которая ему соответствует, после чего осуществлять возведение в стeпeнь.
В заключение, отдельно остановимся на возведении в 1-ую cтепень. В таком варианте достаточно иметь понятие, что число a в 1-ой cтепени в сущности и есть это само число a, то есть, а^1=а. Это представляет частный случай формулы при n равном 1. К примеру, (-9)^1= -9.
Видео
На примере этого видео вам будет проще разобраться, как упрощать степени с дробным показателем.
Источник статьи: http://liveposts.ru/articles/education-articles/matematika/kak-vozvesti-chislo-v-naturalnuyu-i-drobnuyu-stepen
Степень с рациональным показателем
Мы уже знакомы с понятием степени с целым показателем. Давайте разберемся, что такое степень с рациональным показателем.
Рациональный показатель – это выражение вида \(\frac
\), где \(p\)-некоторое целое число, а \(q\) – натуральное число, причем \(q\ge2\).
Положительное число \(a\) в рациональной степени \(\frac
\) является арифметическим корнем степени \(q\) из числа \(a\) в степени \(p\):
Обращаем ваше внимание, что
Неважно в каком порядке – сначала извлечь корень или возвести в степень, от этого смысл выражения не теряется. Как удобнее, так и считайте.
Пусть есть некоторое положительное число \(a\) и целое число \(p\), тогда справедливы следующие соотношения:
где \(k\) и \(q\) – натуральные числа большие 1.
Давайте попробуем их доказать:
Из определения степени с рациональным показателем следует, что:
Опять из определения и свойства корня n-й степени следует:
Третья формула на наш взгляд очевидна, просто сократить степень справа и получите исходное выражение.
Свойства степени с рациональным показателем
Пусть \(a\) и \(b\) – некоторые положительные числа, а числа \(m\) и \(n\) – рациональные числа. Тогда выполняются соотношения:
При умножении степеней с рациональным показателем и одинаковым основанием их показатели степени складываются.
При делении степеней с рациональным показателем и одинаковым основанием их показатели степени вычитаются.
При возведении степени с рациональным показателем в степень с рациональным показателем их показатели перемножаются.
Степень с рациональным показателем от произведения двух положительных чисел равна произведению степеней этих множителей.
Степень с рациональным показателем от частного двух положительных чисел равна частному степеней этих чисел.
И еще два очень важных свойства степеней. Они вам понадобятся при решении показательных уравнений и неравенств.
Пусть опять есть некоторое положительное число \(a>1\) и рациональные числа \(n\) и \(m\).
Если же \(a \gt 1\) и \(n \gt m\), то
Если \( 0 \lt a \lt 1 \) и \(n \gt m\), то
Разберем несколько примеров:
Так как основание степени больше единицы \(3 \gt 1\) и \(\frac<1> <3>\lt \frac<1><2>\).
Так как \(0 \lt \frac<1> <5>\lt 1\) и \(\frac<1> <3>\lt \frac<1><2>\)
Описание урока
От успешной сдачи государственного экзамена по математике зависит поступление в высшее учебное заведение. Степень с рациональным показателем – важная тема, изучение которой необходимо для успешной подготовки к ЕГЭ. От того, насколько хорошо она освоена, зависит в будущем, насколько легко будет решать уравнения и производить более сложные операции с числами. Задание номер 15 строится на умении работать с такими степенями. Чтобы понимать, о чём идёт речь, стоит ознакомиться с определением степени с рациональным показателем и её основными свойствами, которые пригодятся и при работе с функциями.
Степенью числа А, рациональный показатель которого равен p делённому на q, называют выражение, где под корнем степени q находится возведённое в степень p число A. Чтобы более наглядно рассмотреть это явление, разберём пример. Допустим, число 3 возводится в степень 2/4. Тогда изначальное выражение приобретёт следующий вид: корень четвертой степени от 3 в квадрате. 3 во второй степени — 9. Корень четвертой степени из 9 сложно рассчитать без помощи калькулятора, но существуют примеры, где корень n-ой степени из подкоренного выражения легко извлекается.
Важно запомнить, что число А не должно быть меньше 0, а число q не равно 1.
Свойства степени с рациональным показателем
Знание свойств степеней с показателем, равным рациональному числу, облегчает работу с уравнениями и функциями, где содержатся такие выражения. Внимательно их изучив, можно достаточно быстро выполнять задания, что немаловажно в процессе написания ЕГЭ.
Одно из основных свойств: произведение двух степеней с одинаковым основанием равно основанию в степени, равной сумме степеней двух множителей.
При делении степеней с рациональным показателем из показателя делимого вычитают показатель делителя. У степени с рациональным показателем есть и другие свойства, которые также присущи степени с обыкновенным показателем. Их легко запомнить, а чтобы примеры помогли внимательнее рассмотреть свойства, посмотрите видео, в котором о них рассказывается подробнее.
Источник статьи: http://sigma-center.ru/rational_exponent